2020_2021学年新教材高中数学第五章三角函数5

2020_2021学年新教材高中数学第五章三角函数5

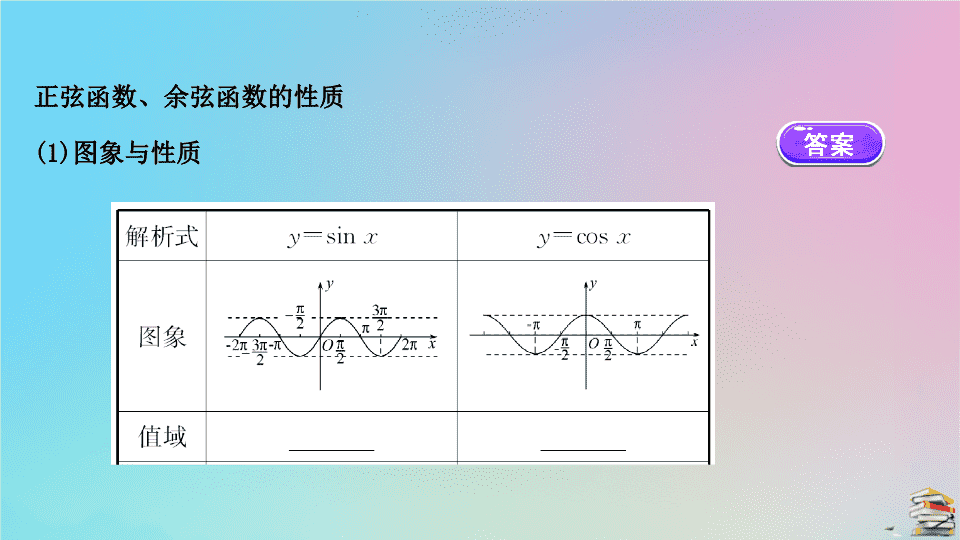
5.4.2　正弦函数、余弦函数的 性质(二)　　 必备知识·自主学习 正弦函数、余弦函数的性质 (1)图象与性质 (2)本质：函数的单调递增、单调递减是描述图象上升、下降的性质. (3)应用：求函数的单调区间、函数的最值及取得最值时自变量x的值. 【思考】 从图象的变化趋势来看，正弦、余弦函数的最大值、最小值点分别处在什么位 置？ 提示：正弦、余弦函数的最大值、最小值点均处于图象拐弯的地方. 【基础小测】 1.辨析记忆(对的打“√”，错的打“×”) (1)y=sin x在(0，π)上单调递增. (　　) (2)存在x∈R满足sin x= . (　　) (3)在区间[0，2π]上，函数y=cos x仅当x=0时取得最大值1. (　　) 提示：(1)×.y=sin x在 上单调递增，在 上单调递减. (2)×.正弦函数y=sin x的值域为[-1，1]，所以sin x= 无解. (3)×.当x=2π时，cos x=1也成立. 2.(教材二次开发：例题改编)函数y=2-sin x取得最大值时，x的取值集合为 _______.  【解析】当sin x=-1时，ymax=2-(-1)=3， 此时x=2kπ- ，k∈Z. 答案： 3.若cos x=m-1有意义，则m的取值范围是_______.  【解析】因为-1≤cos x≤1，要使cos x=m-1有意义， 则-1≤m-1≤1，所以0≤m≤2. 答案：[0，2] 关键能力·合作学习 类型一　正弦函数、余弦函数的单调区间(数学运算) 【题组训练】 1.下列函数，在 上单调递增的是 (　　)　　　　　　　　　　　　　　　　　 A.y=sin x B.y=cos x C.y=sin 2x D.y=cos 2x 2.函数y=sin ，x∈ 的单调递减区间为_______.  3.求函数y=1+sin ，x∈[-4π，4π]的单调递减区间. 【解析】1.选D.对于A，B，C，在 上显然都不是单调递增的，对于函 数y=cos 2x，令π+2kπ≤2x≤2π+2kπ(k∈Z)，即 +kπ≤x≤π+kπ(k∈ Z)，故y=cos 2x的单调递增区间是 (k∈Z)，则当k=0时，单调 递增区间为 2.由 +2kπ≤3x+ ≤ +2kπ(k∈Z)， 得 又x∈ 所以函数y=sin ，x∈ 的单调递减区间为 . 答案： 3.y=1+sin =-sin +1. 由2kπ- ≤ x- ≤2kπ+ (k∈Z). 解得4kπ- ≤x≤4kπ+ π(k∈Z). 又因为x∈[-4π，4π]， 所以函数y=1+sin 的单调递减区间为 【解题策略】 单调区间的求法 求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)的函数的单调区间，要先把ω化为正 数， (1)当A>0时，把ωx+φ整体代入y=sin x或y=cos x的单调递增区间内，求得的x 的范围即为函数的单调递增区间. (2)当A<0时，把ωx+φ整体代入y=sin x或y=cos x的单调递增区间内，求得的 x的范围即为函数的单调递减区间；代入y=sin x或y=cos x的单调递减区间内， 可求得函数的单调递增区间. 提醒：求函数y=Asin(ωx+φ)的单调区间时，把ωx+φ看作一个整体，借助 y=sin x的单调区间来解决.当A<0或ω<0时，要注意原函数的单调性与y= sin x的单调性的关系. 【补偿训练】 1.函数y=cos x在区间[-π，a]上单调递增，则a的取值范围是_______.  2.已知函数y=cos ，则它的单调递减区间为_______.  【解析】1.因为y=cos x在[-π，0]上是单调递增的，在[0，π]上单调递 减，所以只有-πcos ， 即cos >cos . 2.因为cos 1=sin ，而0< <1< 且y=sin x在 上单调递增， 所以sin cos β 【解析】选B.α，β为锐角三角形的两个内角，α+β> ，α> -β， α∈ ， -β∈ ， 所以cos α0，cos 760°= cos 40°>0且cos 20°>cos 40°，所以cos 150°0).当x∈ 时，f(x)的最大 值为 ，最小值是-2，求a和b的值. 【思路导引】先由x∈ ，求2x- 的取值范围，再求sin 的取值 范围，最后表示出f(x)min，f(x)max，列方程组求解. 【解析】因为 因为a>0，所以f(x)max=a+b= ， f(x)min=- a+b=-2. 【解题策略】 求y=sin(ωx+φ)型三角函数的值域的方法 令t=ωx+φ，根据题中x的取值范围，求出t的取值范围，再利用三角函数的单 调性、有界性求出y=sin t的最值(值域). 1.函数f(x)=-2sin x+1，x∈ 的值域是 (　　) A.[1，3] B.[-1，3] C.[-3，1] D.[-1，1] 【解析】选B.因为x∈ ，所以sin x∈[-1，1]，所以-2sin x+1∈ [-1，3]. 2.函数y=3-4sin x -4cos2x的值域为 _______.  【解析】y=3-4sin x-4cos2x =3-4sin x-4(1-sin2x) =4sin2x-4sin x-1， 令t=sin x，则-1≤t≤1. 所以y=4t2-4t-1=4 -2(-1≤t≤1). 所以当t= 时，ymin=-2， 当t=-1时，ymax=7. 即函数y=3-4sin x-4cos2x的值域为[-2，7]. 答案：[-2，7] 3.若函数y=a-bcos x(b>0)的最大值为 ，最小值为- ，则函数的解析式 为y=_______.  【解析】因为y=a-bcos x(b>0)，所以ymax=a+b= ，ymin=a-b=- . 所以y= -cos x. 答案： -cos x 课堂检测·素养达标 1.(教材二次开发：练习改编)函数y=sin 2x的单调递减区间是 (　　) A. (k∈Z) B. (k∈Z) C.[π+2kπ，3π+2kπ](k∈Z) D. (k∈Z) 【解析】选B.令 +2kπ≤2x≤ +2kπ，k∈Z， 得 +kπ≤x≤ +kπ，k∈Z，则y=sin 2x的单调递减区间是 2.y=2sin 的值域是 (　　)　　　　　　　　　　　　　　　　　　 A.[-2，2] B.[0，2] C.[-2，0] D.[-1，1] 【解析】选A.因为sin ∈[-1，1]， 所以y∈[-2，2]. 3.下列函数中，既为偶函数又在(0，π)上单调递增的是 (　　) A.y=|cos x| B.y=cos|-x| C.y=sin D.y=-sin 【解析】选C.y=|cos x|在 上单调递减，排除A； y=cos |-x|=cos |x|在(0，π)上单调递减.排除B；y=sin =-sin =-cos x是偶函数，且在(0，π)上单调递增，符合题意；y=-sin 在(0，π) 上是单调递减的，排除D. 4.若y=asin x+b的最大值为3，最小值为1，则ab=_______.  【解析】当a>0时， 当a<0时， 所以ab=±2. 答案：±2 5.sin 1，sin 2，sin 3按从小到大排列的顺序为_______.  【解析】因为1< <2<3<π， sin(π-2)=sin 2，sin(π-3)=sin 3. y=sin x在 上单调递增，且0<π-3<1<π-2< ，所以sin(π-3)

查看更多