2015年数学理高考课件2-2 函数的单调性与最值

2015年数学理高考课件2-2 函数的单调性与最值

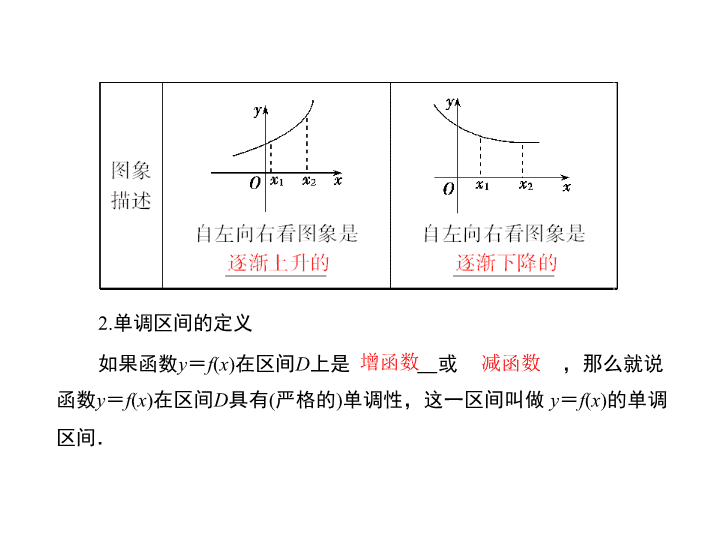
[ 最新考纲展示 ] 　 1 ． 理解函数的单调性、最大值、最小值及其几何意义．　 2. 会运用函数的图象理解和研究函数的性质． 第二节　函数的单调性与最值 函数的单调性 1 ．单调函数的定义 2. 单调区间的定义 如果函数 y ＝ f ( x ) 在区间 D 上是 或 ，那么就说函数 y ＝ f ( x ) 在区间 D 具有 ( 严格的 ) 单调性，这一区间叫做 y ＝ f ( x ) 的单调区间． 增函数 减函数 答案： B 解析： 依据增函数的定义可知，对于 ①③ ，当自变量增大时，相对应的函数值也增大，所以 ①③ 可推出函数 y ＝ f ( x ) 为增函数． 答案： ①③ 函数的最值 ____________________[ 通关方略 ]____________________ 　 求函数最值的常用方法 (1) 单调性法：先确定函数的单调性，再由单调性求最值； (2) 图象法：先作出函数的图象，再观察其最高点，最低点，求出最值； (3) 基本不等式法：先对解析式变形，使之具备 “ 一正二定三相等 ” 的条件后用基本不等式求出最值； (4) 导数法：先求导，然后求出在给定区间上的极值，最后结合端点值，求出最值． (5) 换元法：对比较复杂的函数可通过换元转化为熟悉的函数，再用相应的方法求最值． 答案： D 4 ． f ( x ) ＝ x 2 － 2 x ( x ∈ [ － 2,4]) 的单调增区间为 ________ ； f ( x ) max ＝ ________. 解析： 函数 f ( x ) 的对称轴为 x ＝ 1 ，单调增区间为 [1,4] ，所以 f ( x ) max ＝ f ( － 2) ＝ f (4) ＝ 8. 答案： [1,4] 　 8 函数单调性的判断 答案： B 求函数的单调区间 [ 答案 ] 　 B 反思总结 求函数的单调性或单调区间的方法 (1) 利用已知函数的单调性； (2) 定义法：先求定义域，再利用单调性定义来求； (3) 图象法：如果 f ( x ) 是以图象形式给出的，或者 f ( x ) 的图象易作出，可由图象的直观性写出它的单调区间； (4) 导数法：利用导数取值的正负确定函数的单调区间． 答案： C 由函数的单调性求参数的范围 【 例 3】 　 (1) 定义在 R 上的偶函数 f ( x ) 在 (0 ，＋ ∞ ) 上是增函数，则 ( 　　 ) A ． f (3) ＜ f ( － 4) ＜ f ( － π) B ． f ( － π) ＜ f ( － 4) ＜ f (3) C ． f (3) ＜ f ( － π) ＜ f ( － 4) D ． f ( － 4) ＜ f ( － π) ＜ f (3) [ 解析 ] 　 (1) ∵ f ( x ) 是偶函数， ∴ f ( － π) ＝ f (π) ， f ( － 4) ＝ f (4) ． 又 ∵ f ( x ) 在 (0 ，＋ ∞ ) 上是增函数， ∴ f (3) ＜ f (π) ＜ f (4) ， ∴ f (3) ＜ f ( － π) ＜ f ( － 4) ，故 C 正确． (2) 要保证函数 f ( x ) 在 ( － ∞ ，＋ ∞ ) 上单调递增．则首先要满足分段函数在各自的定义域内分别单调递增．若 f ( x ) ＝ ( a － 2) x － 1 在区间 ( － ∞ ， 1] 上单调递增，则 a － 2>0 ，即 a >2. 若 f ( x ) ＝ log a x 在区间 (1 ，＋ ∞ ) 上单调递增，则 a >1. 另外要保证函数 f ( x ) 在 ( － ∞ ，＋ ∞ ) 上单调递增还需满足 ( a － 2) × 1 － 1 ≤ log a 1 ＝ 0 ，即 a ≤ 3. 故 2< a ≤ 3. [ 答案 ] 　 (1)C 　 (2)2< a ≤ 3 反思总结 单调性的应用常涉及大小比较，解不等式，求最值及已知单调性求参数范围等问题，解决时要注意等价转化思想与数形结合思想的运用． —— 函数的最值问题 函数的最值问题是高考热点内容之一，主要涉及二次型函数最值，基本不等式求最值及应用．常见的方法有换元法、数形结合法． 换元法 解题模板 　 第一步：换元　确定解析式中的某一部分作为一个新的变元 第二步：定范围　根据新的变元的表达式确定新变元的取值范围 M . 第三步：转化　将问题转化为关于新变元的一个函数在区间 M 上的最值问题． 第四步：求最值　利用基本初等函数求最值得原函数的最值． 数形结合法 【 典例 2】 　用 min{ a ， b ， c } 表示 a ， b ， c 三个数中的最小值，则函数 f ( x ) ＝ min{4 x ＋ 1 ， x ＋ 4 ，－ x ＋ 8} 的最大值是 ________ ． [ 解析 ] 　 在同一坐标系中分别作出函数 y ＝ 4 x ＋ 1 ， y ＝ x ＋ 4 ， y ＝－ x ＋ 8 的图象后，取位于下方的部分得函数 f ( x ) ＝ min{4 x ＋ 1 ， x ＋ 4 ，－ x ＋ 8} 的图象，如图所示，不难看出函数 f ( x ) 在 x ＝ 2 时取得最大值 6. 故填 6. [ 答案 ] 　 6 解题模板 　 对于函数解析式有明显的几何特征的函数最值问题，解题步骤是： 第一步：数变形　根据函数解析式的特征，构造图形转化为求几何中的最值． 第二步：解形　利用几何方法解决图形中的最值． 第三步：还形为数　将几何中的最值还原为函数的最值． 第四步：回顾反思　利用数形结合法求解函数最值，其实质就是利用函数图象或借助几何图形求解函数最值，关键在于把握函数解析式的结构特征． 答案： [0 ，＋∞ ) 本小节结束 请按 ESC 键返回