- 2021-06-30 发布 |
- 37.5 KB |
- 43页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2015年数学理高考课件7-5 直线、平面垂直的判定及其性质
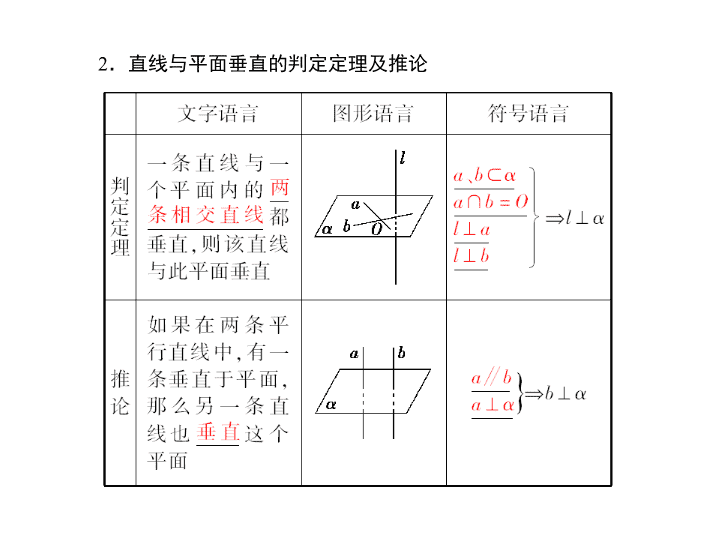
[ 最新考纲展示 ] 1 . 以立体几何的定义、公理和定理为出发点,认识和理解空间中线、面垂直的有关性质与判定定理; 2. 能运用公理、定理和已获得的结论证明一些空间图形垂直关系的简单命题. 第五节 直线、平面垂直的判定及其性质 直线与平面垂直的判定及性质 1 .直线和平面垂直的定义 直线 l 与平面 α 内的 直线都垂直,就说直线 l 与平面 α 互相垂直. 任意一条 2 .直线与平面垂直的判定定理及推论 3. 直线与平面垂直的性质定理 ____________________[ 通关方略 ]____________________ 1 .直线与平面垂直的定义常常逆用,即 a ⊥ α , b ⊂ α ⇒ a ⊥ b . 2 .若平行直线中一条垂直于平面,则另一条也垂直于该平面. 3 .垂直于同一条直线的两个平面平行. 4 .过一点有且只有一条直线与已知平面垂直. 5 .过一点有且只有一个平面与已知直线垂直. 1 .给出下列四个命题: ① 垂直于同一平面的两条直线相互平行; ② 垂直于同一平面的两个平面相互平行; ③ 若一个平面内有无数条直线与另一个平面都平行,那么这两个平面相互平行; ④ 若一条直线垂直于一个平面内的任一直线,那么这条直线垂直于这个平面. 其中真命题的个数是 ( ) A . 1 B . 2 C . 3 D . 4 解析: 命题 ① , ④ 为真,命题 ② , ③ 为假,故选 B. 答案: B 2 .设 l , m , n 为三条不同的直线, α , β 为两个不同的平面,下列命题中正确的是 ( ) A .若 l ⊥ α , m ∥ β , α ⊥ β ,则 l ⊥ m B .若 m ⊂ α , n ⊂ α , l ⊥ m , l ⊥ n ,则 l ⊥ α C .若 l ∥ m , m ∥ n , l ⊥ α ,则 n ⊥ α D .若 m ∥ α , n ∥ β , α ∥ β ,则 m ∥ n 解析: A 项中, l ∥ β 或 l ⊂ β , m 与 l 可能异面或相交,故 A 错误; B 项中,若 m ∥ n ,则无法得出 l ⊥ α ,故 B 错误; C 项中,由 l ∥ m 及 m ∥ n ,可得 l ∥ n ,又 l ⊥ α ,所以 n ⊥ α ,故 C 正确; D 项中, m 与 n 可能相交或异面,故 D 错误.故选 C. 答案: C 平面与平面垂直的判定及性质 1 .平面与平面垂直的判定定理 2 .平面与平面垂直的性质定理 3. 垂直关系的转化 ____________________[ 通关方略 ]____________________ 1 .两个平面互相垂直是两个平面相交的特殊情形. 2 .由平面和平面垂直的判定定理可知,要证明平面与平面垂直,可转化为从现有直线中寻找平面的垂线,即证明线面垂直. 3 .平面和平面垂直的判定定理的两个条件: l ⊂ α , l ⊥ β ,缺一不可. 3 . (2014 年郑州模拟 ) 设 a 、 b 是两条不同的直线, α 、 β 是两个不同的平面,则下列四个命题: ① 若 a ⊥ b , a ⊥ α , b ⊄ α ,则 b ∥ α ; ② 若 a ∥ α , a ⊥ β ,则 α ⊥ β ; ③ 若 a ⊥ β , α ⊥ β ,则 a ∥ α 或 a ⊂ α ; ④ 若 a ⊥ b , a ⊥ α , b ⊥ β ,则 α ⊥ β . 其中正确命题的个数为 ( ) A . 1 B . 2 C . 3 D . 4 解析: 通过线面垂直及平行的判定定理和性质定理,可以判断四个命题都正确,故选 D. 答案: D 4. 如图,在正四面体 P - ABC 中, D 、 E 、 F 分别是 AB 、 BC 、 CA 的中点,下面四个结论不成立的是 ( ) A . BC ∥ 平面 PDF B . DF ⊥ 平面 PAE C .平面 PDF ⊥ 平面 PAE D .平面 BDE ⊥ 平面 ABC 解析: 因 BC ∥ DF ,所以 BC ∥ 平面 PDF , A 成立;易证 BC ⊥ 平面 PAE , BC ∥ DF ,所以结论 B 、 C 均成立;点 P 在底面 ABC 内的射影为 △ ABC 的中心,不在中位线 DE 上,故结论 D 不成立. 答案: D 垂直关系的基本问题 【 例 1】 (1) 设 a , b 是夹角为 30° 的异面直线,则满足条件 “ a ⊂ α , b ⊂ β ,且 α ⊥ β ” 的平面 α , β ( ) A .不存在 B .有且只有一对 C .有且只有两对 D .有无数对 (2) 已知直线 l ⊥ 平面 α ,直线 m ⊂ 平面 β ,有下列命题: ① α ∥ β ⇒ l ⊥ m ; ② α ⊥ β ⇒ l ∥ m ; ③ l ∥ m ⇒ α ⊥ β ; ④ l ⊥ m ⇒ α ∥ β . 其中,正确的命题序号有 ________ . [ 解析 ] (1) 过直线 a 的平面 α 有无数个.当平面 α 与直线 b 平行时,两直线的公垂线与 b 确定的平面 β ⊥ α ;当平面 α 与 b 相交时,过交点作平面 α 的垂线与 b 确定的平面 β ⊥ α ,故选 D. (2) ① 正确, ∵ l ⊥ α , α ∥ β , ∴ l ⊥ β ,又 m ⊂ β , ∴ l ⊥ m ; ② 错误; l , m 还可以垂直,斜交或异面; ③ 正确; ∵ l ⊥ α , l ∥ m , ∴ m ⊥ α ,又 m ⊂ β , ∴ α ⊥ β ; ④ 错误; α 与 β 可能相交. [ 答案 ] (1)D (2) ①③ 反思总结 解决垂直关系的基本问题要注意 (1) 紧扣垂直关系的判定定理与性质定理. (2) 借助于图形去判断. (3) 举反例排除去判断. 变式训练 1 . (2014 年惠州调研 ) 设 α , β 为不重合的平面, m , n 为不重合的直线,则下列命题正确的是 ( ) A .若 α ⊥ β , α ∩ β = n , m ⊥ n ,则 m ⊥ α B .若 m ⊂ α , n ⊂ β , m ⊥ n ,则 n ⊥ α C .若 n ⊥ α , n ⊥ β , m ⊥ β ,则 m ⊥ α D .若 m ∥ α , n ∥ β , m ⊥ n ,则 α ⊥ β 解析: 与 α , β 两垂直相交平面的交线垂直的直线 m ,可与 α 平行,故 A 错误;对 B ,存在 n ∥ α 的情况,故 B 错误;对 D ,存在 α ∥ β 的情况,故 D 错误;由 n ⊥ α , n ⊥ β ,可知 α ∥ β ,又 m ⊥ β ,所以 m ⊥ α ,故 C 正确,选 C. 答案: C 直线与平面垂直的判定与性质 [ 解析 ] (1) 证明: 因为 BC = CD ,即 △ BCD 为等腰三角形, 又 ∠ ACB = ∠ ACD ,故 BD ⊥ AC . 因为 PA ⊥ 底面 ABCD ,所以 PA ⊥ BD . 从而 BD 与平面 PAC 内两条相交直线 PA , AC 都垂直,所以 BD ⊥ 平面 PAC . 解析: 由条件知, BD ⊥ 平面 PAC ,所以 PC ⊥ BD . 又 BC = DC ,故过 D 作 DF ⊥ PC ,连接 BF ,则 BF ⊥ PC , ∴ 存在点 F 使 PC ⊥ 面 BDF . 反思总结 证明直线和平面垂直的常用方法有 (1) 利用判定定理; (2) 利用判定定理的推论 ( a ∥ b , a ⊥ α ⇒ b ⊥ α ) ; (3) 利用面面平行的性质 ( a ⊥ α , α ∥ β ⇒ a ⊥ β ) ; (4) 利用面面垂直的性质. 当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面. 解析: (1) 证明:因为 AB = AC , D 是 BC 的中点,所以 AD ⊥ BC . ① 又在直三棱柱 ABC - A 1 B 1 C 1 中, BB 1 ⊥ 平面 ABC ,而 AD ⊂ 平面 ABC ,所以 AD ⊥ BB 1 . ② 由 ① , ② 得 AD ⊥ 平面 BB 1 C 1 C . 由点 E 在棱 BB 1 上运动,得 C 1 E ⊂ 平面 BB 1 C 1 C ,所以 AD ⊥ C 1 E . 平面与平面垂直的判定与性质 【 例 3】 (2014 年商丘质检 ) 如图,在平行四边形 ABCD 中, AB = 2 BC = 4 , ∠ ABC = 120° , E , M 分别为 AB , DE 的中点,将 △ ADE 沿直线 DE 翻折成 △ A ′ DE , F 为 A ′ C 的中点, A ′ C = 4. (1) 求证:平面 A ′ DE ⊥ 平面 BCD ; (2) 求证: FB ∥ 平面 A ′ DE . [ 证明 ] (1) 由题意, △ A ′ DE 是 △ ADE 沿 DE 翻折而成的, ∴△ A ′ DE ≌△ ADE . ∵∠ ABC = 120° ,四边形 ABCD 是平行四边形, ∴∠ A = 60°. 又 ∵ AD = AE = 2 , ∴△ A ′ DE 和 △ ADE 都是等边三角形. 如图,连接 A ′ M , MC , ∵ M 是 DE 的中点, (2) 取 DC 的中点 N ,连接 FN , NB . ∵ A ′ C = DC = 4 , F , N 分别是 A ′ C , DC 的中点, ∴ FN ∥ A ′ D . 又 ∵ N , E 分别是平行四边形 ABCD 的边 DC , AB 的中点, ∴ BN ∥ DE . 又 ∵ A ′ D ∩ DE = D , FN ∩ NB = N , ∴ 平面 A ′ DE ∥ 平面 FNB . ∵ FB ⊂ 平面 FNB , ∴ FB ∥ 平面 A ′ DE . 反思总结 1 . 判定面面垂直的方法 (1) 面面垂直的定义; (2) 面面垂直的判定定理 ( a ⊥ β , a ⊂ α ⇒ α ⊥ β ) . 2 .在已知平面垂直时,一般要用性质定理进行转化. 在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直. 变式训练 3. 如图,在四棱锥 P - ABCD 中,平面 PAD ⊥ 平面 ABCD , AB = AD , ∠ BAD = 60° , E , F 分别是 AP , AD 的中点. 求证: (1) 直线 EF ∥ 平面 PCD ; (2) 平面 BEF ⊥ 平面 PAD . 证明: (1) 在 △ PAD 中,因为 E , F 分别为 AP , AD 的中点,所以 EF ∥ PD . 又因为 EF ⊄ 平面 PCD , PD ⊂ 平面 PCD , 所以直线 EF ∥ 平面 PCD . (2) 连接 BD . 因为 AB = AD , ∠ BAD = 60° ,所以 △ ABD 为正三角形.因为 F 是 AD 的中点,所以 BF ⊥ AD . 因为平面 PAD ⊥ 平面 ABCD , BF ⊂ 平面 ABCD , 平面 PAD ∩ 平面 ABCD = AD ,所以 BF ⊥ 平面 PAD . 又因为 BF ⊂ 平面 BEF ,所以平面 BEF ⊥ 平面 PAD . —— 平行与垂直的综合问题 空间线面平行,垂直的综合问题一直是命题的热点,多以解答题形式考查,此类题目重点考查了线、面、平行,垂直的判定与性质,解答时易忽视平行垂直判定与性质定理中满足条件. 【 典例 】 (2013 年高考北京卷 )( 本题满分 14 分 ) 如图,在四棱锥 P - ABCD 中, AB ∥ CD , AB ⊥ AD , CD = 2 AB ,平面 PAD ⊥ 底面 ABCD , PA ⊥ AD , E 和 F 分别是 CD 和 PC 的中点.求证: (1) PA ⊥ 底面 ABCD ; (2) BE ∥ 平面 PAD ; (3) 平面 BEF ⊥ 平面 PCD . [ 教你快速规范审题 ] 1 .审条件,挖解题信息 2 .审结论,明解题方向 3 .建联系,找解题突破口 [ 教你准确规范解答 ] (1) 因为平面 PAD ⊥ 底面 ABCD ,且 PA 垂直于这两个平面的交线 AD , 所以 PA ⊥ 底面 ABCD .3 分 (2) 因为 AB ∥ CD , CD = 2 AB , E 为 CD 的中点, 所以 AB ∥ DE ,且 AB = DE .4 分 所以 ABED 为平行四边形. 所以 BE ∥ AD .6 分 又因为 BE ⊄ 平面 PAD , AD ⊂ 平面 PAD , 所以 BE ∥ 平面 PAD .8 分 (3) 因为 AB ⊥ AD ,而且 ABED 为平行四边形. 所以 BE ⊥ CD , AD ⊥ CD , 10 分 由 (1) 知 PA ⊥ 底面 ABCD . 所以 PA ⊥ CD . 所以 CD ⊥ 平面 PAD . 所以 CD ⊥ PD .12 分 因为 E 和 F 分别是 CD 和 PC 的中点, 所以 PD ∥ EF . 又因为 CD ⊥ EF . EF ∩ BE = E , 所以 CD ⊥ 平面 BEF .13 分 所以平面 BEF ⊥ 平面 PCD .14 分 [ 常见失分探因 ] 易漏写 BE ⊄ 平面 PAD , AD ⊂ 平面 PAD 而失分 _______________ [ 教你一个万能模板 ] _________________ 本小节结束 请按 ESC 键返回查看更多