【数学】2018届一轮复习北师大版第一章集合与常用逻辑用语第一节集合教案
第一节 集合
☆☆☆2017考纲考题考情☆☆☆
考纲要求
真题举例
命题角度
1.了解集合的含义,元素与集合的属于关系;能用列举法或描述法表示集合;
2.理解集合之间包含与相等的含义,能识别给定集合的子集;了解全集与空集的含义;
3.理解并会求并集、交集、补集;能用Venn(韦恩)图表达集合的关系与运算。
2016,全国卷Ⅰ,1,5分(集合的交集)
2016,全国卷Ⅱ,2,5分(集合的并集)
2015,全国卷Ⅱ,1,5分(集合的交集)
2014,全国卷Ⅰ,1,5分(集合的交集)
2014,全国卷Ⅱ,1,5分(集合的交集)
主要考查具体集合(能确定集合中元素)的基本运算,偶尔涉及集合间的关系及新定义问题。
微知识 小题练
自|主|排|查
1.集合的含义与表示方法
(1)集合的含义:研究对象叫做元素,一些元素组成的总体叫做集合。集合中元素的性质:确定性、无序性、互异性。
(2)元素与集合的关系:①属于,记为∈;②不属于,记为∉。
(3)集合的表示方法:列举法、描述法和图示法。
(4)常用数集的记号:自然数集N,正整数集N*或N+,整数集Z,有理数集Q,实数集R。
2.集合间的基本关系
表示
关系
文字语言
符号语言
记法
基本关系
子集
集合A中的元素都是集合B中的元素
x∈A⇒x∈B
A⊆B
或B⊇A
真子集
集合A是集合B的子集,且集合B中至少有一个元素不属于A
A⊆B,且∃x0∈B,x0∉A
AB或
BA
相等
集合A,B的元素完全相同
A⊆B,B⊆A
A=B
空集
不含任何元素的集合。空集是任何集合A的子集
∀x,x∉∅,∅⊆A
∅
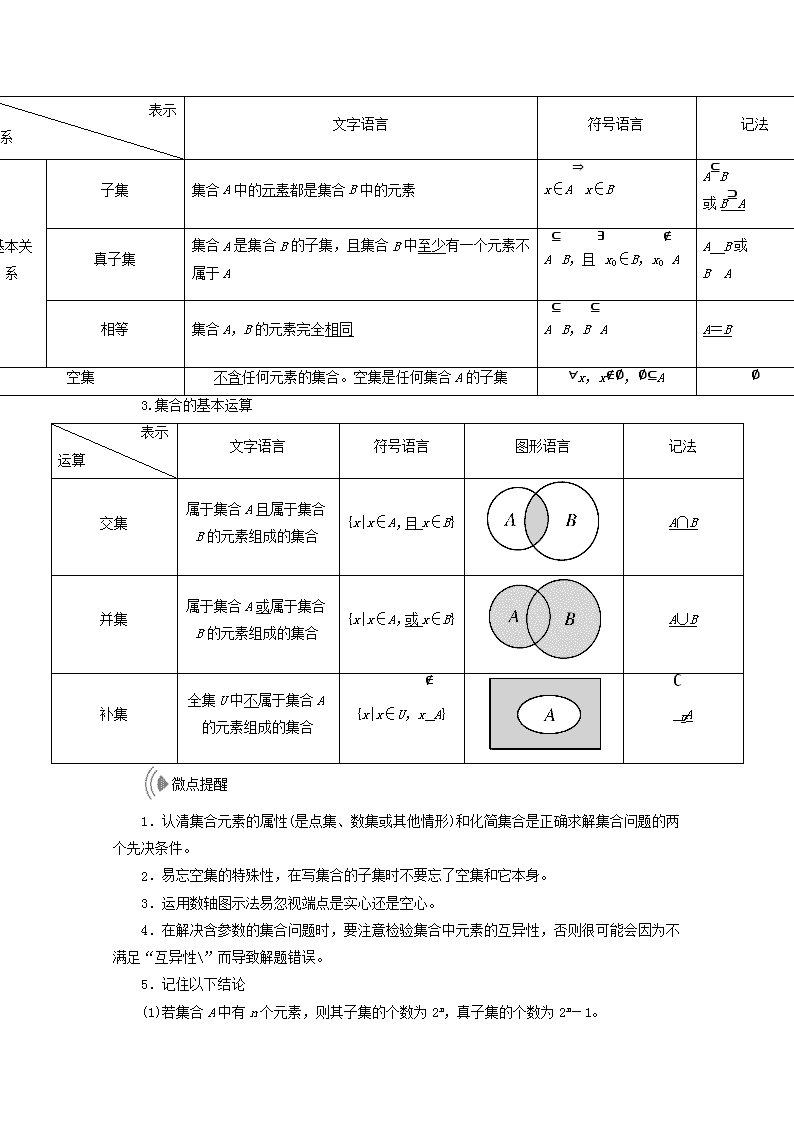
3.集合的基本运算
表示
运算
文字语言
符号语言
图形语言
记法
交集
属于集合A且属于集合B的元素组成的集合
{x|x∈A,且x∈B}
A∩B
并集
属于集合A或属于集合B的元素组成的集合
{x|x∈A,或x∈B}
A∪B
补集
全集U中不属于集合A的元素组成的集合
{x|x∈U,x∉A}
∁UA
微点提醒
1.认清集合元素的属性(是点集、数集或其他情形)和化简集合是正确求解集合问题的两个先决条件。
2.易忘空集的特殊性,在写集合的子集时不要忘了空集和它本身。
3.运用数轴图示法易忽视端点是实心还是空心。
4.在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则很可能会因为不满足“互异性”而导致解题错误。
5.记住以下结论
(1)若集合A中有n个元素,则其子集的个数为2n,真子集的个数为2n-1。
(2)A∪B=A⇔B⊆A;A∩B=A⇔A⊆B。
小|题|快|练
一 、走进教材
1.(必修1P12B组T4改编)满足{0,1}⊆A{0,1,2,3}的集合A的个数为( )
A.1 B.2
C.3 D.4
【解析】 由题意得A可为{0,1},{0,1,2},{0,1,3}。故选C。
【答案】 C
2.(必修1P12B组T1改编)已知集合A={0,1,2},集合B满足A∪B={0,1,2},则集合B有________个。
【解析】 由题意知B⊆A,则集合B有8个。
【答案】 8
二、双基查验
1.已知集合M={-1,0,1},N={0,1,2},则M∪N=( )
A.{-1,0,1} B.{-1,0,1,2}
C.{-1,0,2} D.{0,1}
【解析】 M∪N表示属于M或属于N的元素构成的集合,故M∪N={-1,0,1,2}。故选B。
【答案】 B
2.设集合M={x|x≥0,x∈R},N={x|x2<1,x∈R},则M∩N=( )
A.[0,1] B.[0,1)
C.(0,1] D.(0,1)
【解析】 ∵x2<1,∴-1
0},且1∉A,则实数a的取值范围是( )
A.(-∞,0] B.(-∞,1]
C.[1,+∞) D.[0,+∞)
(2)已知集合A={x2+x,4x},若0∈A,则x=____。
【解析】 (1)若1∈A,则1-2+a>0,解得a>1。因为1∉A,所以a≤1。故选B。
(2)由题意,得或
解得x=-1。
【答案】 (1)B (2)-1
考点二
集合的基本关系…………母题发展
【典例2】 (1)已知集合A={x|x2-2x-3≤0,x∈N*},则集合A的真子集的个数为( )
A.7 B.8
C.15 D.16
(2)(2017·襄阳模拟)已知集合A={x|-2≤x≤7},B={x|m+10},若A⊆B,则实数c的取值范围是( )
A.(0,1] B.[1,+∞)
C.(0,1) D.(1,+∞)
【解析】 (1)因为x⊆A,所以B={∅,{0},{1},{0,1}},则集合A={0,1}是集合B中的元素,所以A∈B。故选D。
(2)解法一:由题意知,A={x|y=lg(x-x2)}={x|x-x2>0}=(0,1),B={x|x2-cx<0,c>0}=(0,c)。
由A⊆B,画出数轴,如图所示,得c≥1。故选B。
解法二:因为A={x|y=lg(x-x2)}={x|x-x2>0}=(0,1),取c=1,则B=(0,1),所以A⊆B成立,可排除C,D;取c=2,则B=(0,2),所以A⊆B成立,可排除A。故选B。
【答案】 (1)D (2)B
考点三
集合的运算…………多维探究
角度一:两个集合的交集、并集、补集运算
【典例3】 (1)(2016·全国卷Ⅱ)已知集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∪B=( )
A.{1} B.{1,2}
C.{0,1,2,3} D.{-1,0,1,2,3}
(2)(2016·天津高考)已知集合A={1,2,3,4},B={y|y=3x-2,x∈A},则A∩B=( )
A.{1} B.{4}
C.{1,3} D.{1,4}
(3)设全集U=R,集合A={x|x≥2},B={y|y=lg(x2+1)},则(∁UA)∩B=( )
A.{x|x≤-1或x≥0}
B.{(x,y)|x≤-1,y≥0}
C.{x|x≥0}
D.{x|x>-1}
【解析】 (1)由已知可得B={x|(x+1)(x-2)<0,x∈Z}={x|-1-1
【解析】 (1)由A∪B=A得B⊆A,有m∈A,所以有m=或m=3,即m=3或m=1或m=0,又由集合中元素的互异性知m≠1。故选B。
(2)∵M={x|-1≤x<2},N={y|y-1即可。故选D。
【答案】 (1)B (2)D
角度三:抽象的集合运算
【典例5】 设U为全集,A,B是集合,则“存在集合C使得A⊆C,B⊆∁UC”是“A∩B=∅”的( )
A.充分而不必要的条件
B.必要而不充分的条件
C.充要条件
D.既不充分也不必要的条件
【解析】 由图可知,若“存在集合C,使得A⊆C,B⊆∁UC”,则一定有“A∩B=∅”;反过来,若“A∩B=∅”,则一定能找到集合C,使A⊆C且B⊆∁UC。故选C。
【答案】 C
反思归纳 集合的基本运算的关注点
1.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提。
2.有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决。
3.注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn图。
4.根据集合运算结果求参数,先把符号语言译成文字语言,然后应用数形结合求解。
微考场 新提升
1.(2016·四川高考)设集合A={x|-2≤x≤2},Z为整数集,则集合A∩Z中元素的个数是( )
A.3 B.4
C.5 D.6
解析 由集合A={x|-2≤x≤2},易知A∩Z={-2,-1,0,1,2}。故选C。
答案 C
2.(2016·全国卷Ⅰ)设集合A={x|x2-4x+3<0},B={x|2x-3>0},则A∩B=( )
A. B.
C. D.
解析 由题意得,A={x|1},
则A∩B=。故选D。
答案 D
3.设全集U是自然数集N,集合A={x|x2>4,x∈N},B={0,2,3},则图中阴影部分所表示的集合是( )
A.{x|x>2,x∈N} B.{x|x≤2,x∈N}
C.{0,2} D.{1,2}
解析 由题图可知,图中阴影部分所表示的集合是B∩(∁UA),∁UA={x|x2≤4,x∈N}={x|-2≤x≤2,x∈N}={0,1,2},∵B={0,2,3},∴B∩(∁UA)={0,2}。故选C。
答案 C
4.(2016·辽宁五校联考)已知集合M,N,P为全集U的子集,且满足M⊆P⊆N,则下列结论不正确的是( )
A.∁UN⊆∁UP B.∁NP⊆∁NM
C.(∁UP)∩M=∅ D.(∁UM)∩N=∅
解析 根据已知条件画出韦恩图结合各选项知,只有D不正确。故选D。
答案 D
5.当两个集合有公共元素,且互不为对方的子集时,我们称这两个集合“相交”。对于集合M={x|ax2-1=0,a>0},N={-,,1},若M与N“相交”,则a=________。
解析 M=,由=,得a=4;由=1,得a=1。
当a=4时,M={-,},此时M⊆N,不合题意;当a=1时,M={-1,1},满足题意。
答案 1
微专题 巧突破
集合中新情境型问题
与集合有关的新概念问题属于信息迁移类问题,它是化归思想的具体运用,是近几年高考的热点问题,这类试题的特点是:通过给出的新的数学概念或新的运算法则,在新的情境下完成某种推理证明,或在新的运算法则下进行运算。常见的有定义新概念、新公式、新运算和新法则等类型。解决此类题的关键是理解问题中的新概念、新公式、新运算、新法则等的含义,然后分析题目中的条件,设法进行套用。
1.定义新概念、新公式
【典例1】 设A是整数集的一个非空子集,对于k∈A,如果k-1∉A且k+1∉A,那么k是A的一个“单一元”,给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“单一元”的集合共有________个。
【解析】 符合题意的集合为{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,6,7},{6,7,8},共6个。
【答案】 6
【变式训练1】 若x∈A,则∈A,就称A是伙伴关系集合,集合M={-1,0,,2,3}的所有非空子集中具有伙伴关系的集合的个数是( )
A.1 B.3
C.7 D.31
【解析】 具有伙伴关系的元素组是-1,,2,所以具有伙伴关系的集合有3个:{-1},,。故选B。
【答案】 B
2.定义新运算、新法则
【典例2】 设A,B是有限集,定义d(A,B)=card(A∪B)-card(A∩B),其中card(A)表示有限集A中的元素个数。
命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;
命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C),
A.命题①和命题②都成立
B.命题①和命题②都不成立
C.命题①成立,命题②不成立
D.命题①不成立,命题②成立
【解析】 命题①显然正确,通过如图韦恩图亦可知d(A,C)表示的区域不大于d(A,B)+d(B,C)的区域,故命题②也正确,故选A。
【答案】 A
【变式训练2】 定义集合的差集运算为A-B={x|x∈A且x∉B},若A={y|y=|x-1|-|x+1|,x∈R},B={y|y=-,x∈R},则A-B=________。
【解析】 先求出集合A,B,再利用差集的定义求A-B。
依题意知,y=|x-1|-|x+1|=
可知-2≤y≤2,所以A=[-2,2]。易知y=-=
在(1,+∞)上单调递减,则0<-≤,即0
查看更多