2021届高考数学一轮总复习课时作业46直线平面平行的判定及其性质含解析苏教版

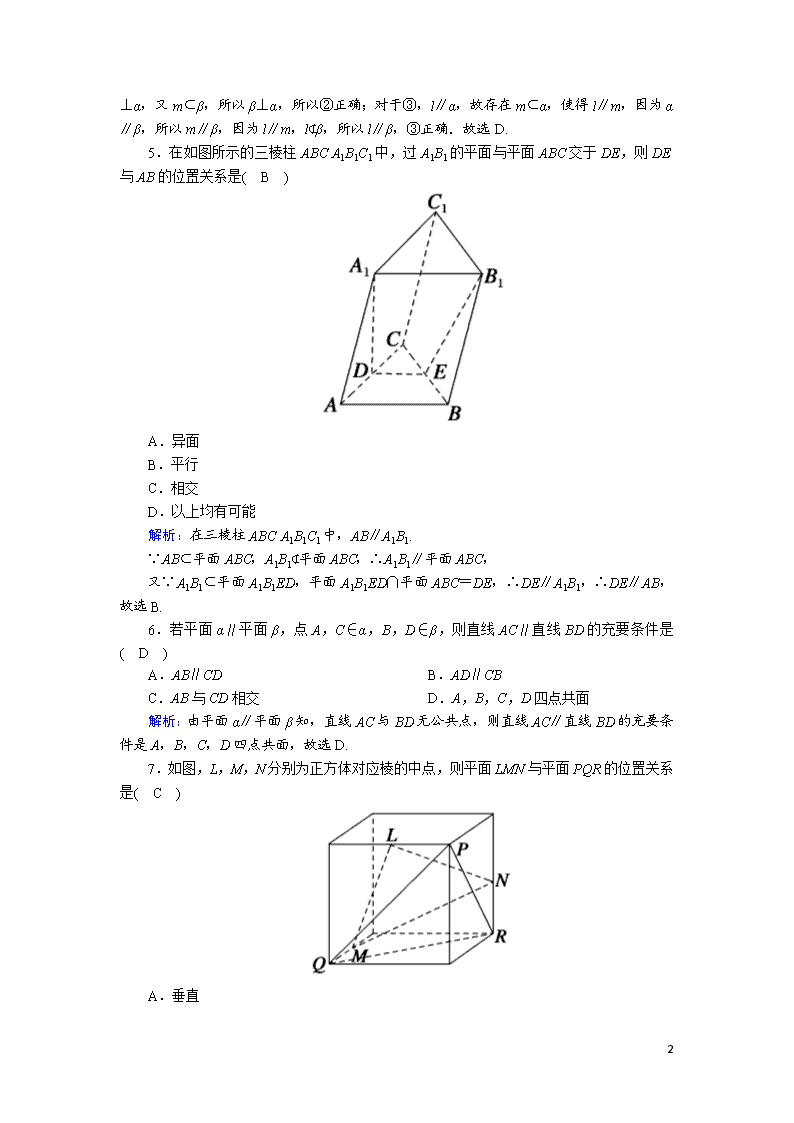
2021届高考数学一轮总复习课时作业46直线平面平行的判定及其性质含解析苏教版

课时作业46　直线、平面平行的判定及其性质 一、选择题 ‎1．如果直线a∥平面α，那么直线a与平面α内的(　D　)‎ A．一条直线不相交 B．两条直线不相交 C．无数条直线不相交 D．任意一条直线都不相交 解析：因为直线a∥平面α，所以直线a与平面α无公共点，所以直线a和平面α内的任意一条直线都不相交，故选D.‎ ‎2．(2020·福州质检)下列说法中，错误的是(　D　)‎ A．一条直线与两个平行平面中的一个相交，则必与另一个平面相交 B．平行于同一平面的两个不同平面平行 C．若直线l与平面α平行，则过平面α内一点和直线l平行的直线在α内 D．若直线l不平行于平面α，则在平面α内不存在与l平行的直线 解析：如果已知直线与另一个平面不相交，则有两种情形：直线在平面内或与平面平行，不管哪种情形都得出这条直线与第一个平面不能相交，出现矛盾，即A中说法正确；选项B是两个平面平行的一种判定方法，即B中说法正确；由线面平行的性质定理知C中说法正确；选项D中说法是错误的，事实上，直线l不平行于平面α，可能有l⊂α，则α内有无数条直线与l平行．故选D.‎ ‎3．(2019·全国卷Ⅱ)设α，β为两个平面，则α∥β的充要条件是(　B　)‎ A．α内有无数条直线与β平行 B．α内有两条相交直线与β平行 C．α，β平行于同一条直线 D．α，β垂直于同一平面 解析：对于A，α内有无数条直线与β平行，当这无数条直线互相平行时，α与β可能相交，所以A不正确；对于B，根据两平面平行的判定定理与性质知，B正确；对于C，平行于同一条直线的两个平面可能相交，也可能平行，所以C不正确；对于D，垂直于同一平面的两个平面可能相交，也可能平行，如长方体的相邻两个侧面都垂直于底面，但它们是相交的，所以D不正确．综上可知选B.‎ ‎4．已知α，β，γ是三个不重合的平面，l是直线．给出下列命题：①若l上两点到α的距离相等，则l∥α；②若l⊥α，l∥β，则α⊥β；③若α∥β，l⊄β，且l∥α，则l∥β.其中正确的命题是(　D　)‎ A．①② B．①②③‎ C．①③ D．②③‎ 解析：对于①，若直线l在平面α内，l上有两点到α的距离为0，相等，此时l不与α平行，所以①错误；对于②，因为l∥β，所以存在直线m⊂β使得l∥m，因为l⊥α，所以m 8‎ ‎⊥α，又m⊂β，所以β⊥α，所以②正确；对于③，l∥α，故存在m⊂α，使得l∥m，因为α∥β，所以m∥β，因为l∥m，l⊄β，所以l∥β，③正确．故选D.‎ ‎5．在如图所示的三棱柱ABCA1B‎1C1中，过A1B1的平面与平面ABC交于DE，则DE与AB的位置关系是(　B　)‎ A．异面 B．平行 C．相交 D．以上均有可能 解析：在三棱柱ABCA1B‎1C1中，AB∥A1B1.‎ ‎∵AB⊂平面ABC，A1B1⊄平面ABC，∴A1B1∥平面ABC，‎ 又∵A1B1⊂平面A1B1ED，平面A1B1ED∩平面ABC＝DE，∴DE∥A1B1，∴DE∥AB，故选B.‎ ‎6．若平面α∥平面β，点A，C∈α，B，D∈β，则直线AC∥直线BD的充要条件是(　D　)‎ A．AB∥CD B．AD∥CB C．AB与CD相交 D．A，B，C，D四点共面 解析：由平面α∥平面β知，直线AC与BD无公共点，则直线AC∥直线BD的充要条件是A，B，C，D四点共面，故选D.‎ ‎7．如图，L，M，N分别为正方体对应棱的中点，则平面LMN与平面PQR的位置关系是(　C　)‎ A．垂直 8‎ B．相交不垂直 C．平行 D．重合 解析：如图，分别取另三条棱的中点A，B，C，将平面LMN延展为平面正六边形AMBNCL，因为PQ∥AL，PR∥AM，且PQ与PR相交，AL与AM相交，所以平面PQR∥平面AMBNCL，即平面LMN∥平面PQR.‎ ‎8．已知平面α∥平面β，P是α，β外一点，过点P的直线m与α，β分别交于点A，C，过点P的直线n与α，β分别交于点B，D，且PA＝6，AC＝9，PD＝8，则BD的长为(　B　)‎ A．16 B．24或 C．14 D．20‎ 解析：设BD＝x，由α∥β⇒AB∥CD⇒△PAB∽△PCD⇒＝.(1)当点P在两平面之间时，如图①，则有＝，∴x＝24；(2)当点P在两平面外侧时，如图②，则有＝，∴x＝.故选B.‎ 二、填空题 ‎9.如图，四棱锥PABCD的底面是直角梯形，AB∥CD，BA⊥AD，CD＝2AB，PA⊥底面ABCD，E为PC的中点，则BE与平面PAD的位置关系为平行．‎ 8‎ 解析：取PD的中点F，连接EF，AF.‎ 在△PCD中，EF＝CD且EF∥CD.‎ 又∵AB∥CD且CD＝2AB，∴EF綊AB，‎ ‎∴四边形ABEF是平行四边形，∴EB∥AF.‎ 又∵EB⊄平面PAD，AF⊂平面PAD，∴BE∥平面PAD.‎ ‎10．如图是长方体被一平面截得的几何体，四边形EFGH为截面，则四边形EFGH的形状为平行四边形．‎ 解析：∵平面ABFE∥平面DCGH，平面EFGH∩平面ABFE＝EF，平面EFGH∩平面DCGH＝HG，∴EF∥HG.同理，EH∥FG，∴四边形EFGH是平行四边形．‎ ‎11．(2020·豫北名校联考)在斜三棱柱ABCA1B‎1C1中，点D，D1分别为AC，A‎1C1上的点，若平面BC1D∥平面AB1D1，则＝1.‎ 解析：如图所示，连接A1B，与AB1交于点O，连接OD1，∵平面BC1D∥平面AB1D1，平面BC1D∩平面A1BC1＝BC1，平面A1BC1∩平面AB1D1＝D1O，∴BC1∥D1O，‎ 8‎ ‎∴＝，同理AD1∥DC1，‎ ‎∴＝，∴＝，‎ 又∵＝1，∴＝1，即＝1.‎ ‎12．(2020·河南安阳模拟)如图所示，在长方体ABCD‎ A1B‎1C1D1中，AB＝AD＝2，AA1＝1.一平面截该长方体，所得截面为OPQRST，其中O，P分别为AD，CD的中点，B1S＝，则AT＝.‎ 解析：设AT＝x，A1T＝y，则x＋y＝1.由题意易知该截面六边形的对边分别平行，即OP∥SR，OT∥QR，PQ∥TS，则△DOP∽△B1SR.又因为DP＝DO＝1，所以B1S＝B1R＝，所以A1S＝C1R＝.由△ATO∽△C1QR，可得＝，所以C1Q＝x.由△A1TS∽△CQP，可得＝，所以CQ＝y，所以x＋y＝x＋y＝1，可得x＝，y＝，所以AT＝.‎ 三、解答题 ‎13．如图，E，F，G，H分别是正方体ABCDA1B‎1C1D1的棱BC，CC1，C1D1，AA1的中点．求证：‎ ‎(1)EG∥平面BB1D1D；‎ ‎(2)平面BDF∥平面B1D1H.‎ 证明：(1)如图，取B1D1的中点O，‎ 8‎ 连接GO，OB，因为OG綊B‎1C1，BE綊B‎1C1，所以BE綊OG，所以四边形BEGO为平行四边形，故OB∥EG，‎ 因为OB⊂平面BB1D1D，EG⊄平面BB1D1D，‎ 所以EG∥平面BB1D1D.‎ ‎(2)由题意可知BD∥B1D1.连接HB，D‎1F，因为BH綊D‎1F，‎ 所以四边形HBFD1是平行四边形，故HD1∥BF.‎ 又B1D1∩HD1＝D1，BD∩BF＝B，‎ 所以平面BDF∥平面B1D1H.‎ ‎14．(2020·南昌摸底)如图，在四棱锥PABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，PA＝2，AB＝1.设M，N分别为PD，AD的中点．‎ ‎(1)求证：平面CMN∥平面PAB；‎ ‎(2)求三棱锥PABM的体积．‎ 解：(1)证明：∵M，N分别为PD，AD的中点，∴MN∥PA，‎ 又MN⊄平面PAB，PA⊂平面PAB，∴MN∥平面PAB.‎ 在Rt△ACD中，∠CAD＝60°，CN＝AN，∴∠ACN＝60°.‎ 又∠BAC＝60°，∴CN∥AB.‎ ‎∵CN⊄平面PAB，AB⊂平面PAB，∴CN∥平面PAB.‎ 又CN∩MN＝N，∴平面CMN∥平面PAB.‎ 8‎ ‎(2)由(1)知，平面CMN∥平面PAB，‎ ‎∴点M到平面PAB的距离等于点C到平面PAB的距离．‎ ‎∵AB＝1，∠ABC＝90°，∠BAC＝60°，∴BC＝，‎ ‎∴三棱锥PABM的体积V＝VMPAB＝VCPAB＝VPABC＝××1××2＝.‎ ‎15．(2020·郑州预测)已知直三棱柱ABCA1B‎1C1的底面为等腰直角三角形，AB⊥AC，点M，N分别是边AB1，A‎1C上的动点，若直线MN∥平面BCC1B1，Q为线段MN的中点，则点Q的轨迹为(　C　)‎ A．双曲线的一支(一部分) B．圆弧(一部分)‎ C．线段(去掉一个端点) D．抛物线的一部分 解析：如图，分别取AA1，B‎1C的中点E，F，任意作一个与平面BCC1B1平行的平面α与AB1，A‎1C分别交于M，N，则MN∥平面BCC1B1.由题意知△ABC为等腰直角三角形，AB⊥AC，则侧面AA1B1B与侧面AA‎1C1C是两个全等的矩形，且这两个侧面关于过棱AA1与平面BCC1B1垂直的平面是对称的，因此EF必过MN的中点Q，故点Q的轨迹为线段EF，但需去掉端点F，故选C.‎ ‎16．(2020·南昌一模)如图，在四棱锥PABCD中，PA⊥底面ABCD，四边形ABCD为直角梯形，AC与BD相交于点O，AD∥BC，AD⊥AB，AB＝BC＝AP＝3，三棱锥PACD的体积为9.‎ 8‎ ‎(1)求AD的值；‎ ‎(2)过O点的平面α平行于平面PAB，平面α与棱BC，AD，PD，PC分别相交于点E，F，G，H，求截面EFGH的周长．‎ 解：(1)因为在四棱锥PABCD中，PA⊥底面ABCD，‎ 四边形ABCD为直角梯形，AD∥BC，AD⊥AB，AB＝BC＝AP＝3.‎ 所以VPACD＝×·AP＝＝9，‎ 解得AD＝6.‎ ‎(2)因为α∥平面PAB，平面α∩平面ABCD＝EF，O∈EF，平面PAB∩平面ABCD＝AB，所以EF∥AB，同理EH∥BP，FG∥AP.‎ 因为BC∥AD，AD＝6，BC＝3，‎ 所以△BOC∽△DOA，且＝＝，‎ 所以＝，CE＝CB＝1，BE＝AF＝2，‎ 同理＝＝＝，所以EH＝PB＝.‎ 同理，FG＝PA＝2.连接HO，则有HO∥PA，‎ 所以HO⊥EO，HO＝1，‎ 过点H作HN∥EF交FG于N，‎ 则GH＝＝，‎ 所以截面EFGH的周长为3＋2＋＋＝5＋＋.‎ 8‎