高中数学选修1-2：2_1_2同步练习

高中数学选修1-2：2_1_2同步练习

高中数学人教A版选修1-2 同步练习 ‎1.“∵四边形ABCD是矩形，∴四边形ABCD的对角线相等．”以上推理的大前提是(　　)‎ A．正方形都是对角线相等的四边形 B．矩形都是对角线相等的四边形 C．等腰梯形都是对角线相等的四边形 D．矩形都是对边平行且相等的四边形 解析：选B.从小前提和结论来看其大前提是矩形都是对角线相等的四边形．‎ ‎2.有一段演绎推理是这样的：“有些有理数是分数，整数是有理数，则整数是分数”．结论显然是错误的，这是因为(　　)‎ A．大前提错误　　　　　　 B．小前提错误 C．推理形式错误 D．非以上错误 解析：选C.大前提“有些有理数是分数”中，M为“有些有理数”，P为“分数”，小前提“整数是有理数”中，S是“整数”，而“有理数”不是大前提中的“M”．‎ ‎3.‎ 如图所示，因为四边形ABCD是平行四边形，‎ 所以AB＝CD，BC＝AD.‎ 又因为△ABC和△CDA的三边对应相等，所以△ABC≌△CDA.‎ 上述推理的两个步骤中应用的推理形式是________．‎ 答案：三段论 ‎4.由“(a2＋a＋1)x>3，得x>”的推理过程中，其大前提是________．‎ 解析：∵a2＋a＋1＝＋>0.∴(a2＋a＋1)x>3⇒x>.‎ 其前提依据为不等式的乘法法则：a>0，b>c⇒ab>ac.‎ 答案：a>0，b>c⇒ab>ac ‎[A级　基础达标]‎ ‎1.命题“有理数是无限循环小数，整数是有理数，所以整数是无限循环小数”是假命题，推理错误的原因是(　　)‎ A．使用了归纳推理 B．使用了类比推理 C．使用了“三段论”，但大前提错误 D．使用了“三段论”，但小前提错误 解析：选C.使用了“三段论”，大前提“有理数是无限循环小数”是错误的．‎ ‎2.在不等边三角形中，a为最大边，要想得到∠A为钝角的结论，三边a、b、c应满足的条件是(　　)‎ A．a2b2＋c2 D．a2≤b2＋c2‎ 解析：选C.由于cosA＝<0，‎ ‎∴b2＋c2－a2<0，∴a2>b2＋c2.‎ ‎3.(2012·菏泽一中高二检测)下列推理过程属于演绎推理的是(　　)‎ A．老鼠、猴子与人在身体结构上大有相似之处，某医药先在猴子身上试验，试验成功后再用于人体试验 B．由1＝12，1＋3＝22，1＋3＋5＝32，…得出1＋3＋5＋…＋(2n－1)＝n2‎ C．由三角形的三条中线交于一点联想到四面体四条中线(四面体每个顶点与对面重心的连线)交于一点 D．通项公式如an＝cqn(c，q≠0)的数列{an}为等比数列，则数列{－2n}为等比数列 解析：选D.A、C是类比推理，B是归纳推理，D是演绎推理．‎ ‎4.补充下列推理的三段论：‎ ‎(1)因为互为相反数的两个数的和为0，又因为a与b互为相反数且________，所以b＝8.‎ ‎(2)因为________，又因为e＝2.71828…是无限不循环小数，所以e是无理数．‎ 答案：(1)a＝－8　(2)无限不循环小数是无理数 ‎5.已知a＝，函数f(x)＝ax，若实数m，n满足f(m)>f(n)，则m，n的大小关系为________．‎ 解析：当0f(n)得mx2，‎ 则f(x1)－f(x2)＝－ ‎＝ ‎＝.‎ ‎∵x1>x2，∴2x1>2x2>0，‎ ‎∴2x1－2x2>0，2x1＋1>0，2x2＋1>0.‎ ‎∴>0.‎ ‎∴f(x1)>f(x2)．‎ ‎∴f(x)在R上为单调递增函数．‎ ‎[B级　能力提升]‎ ‎7.某西方国家流传这样的一个政治笑话：“鹅吃白菜，参议员先生也吃白菜，所以参议员先生是鹅”．结论显然是错误的，这是因为(　　)‎ A．大前提错误 B．小前提错误 C．推理形式错误 D．非以上错误 解析：选C.推理形式不符合三段论推理的形式．三段论的形式是：M是P，S是M，则S是P，而上面的推理形式则是：M是P，S是P，则S是M.‎ 设⊕是R的一个运算，A是R的非空子集．若对于任意a，b∈A，有a⊕b∈A，则称A对运算⊕封闭．下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是(　　)‎ A．自然数集 B．整数集 C．有理数集 D．无理数集 解析：选C.A错：因为自然数集对减法不封闭；B错：因为整数集对除法不封闭；C对：因为任意两个有理数的和、差、积、商都是有理数，故有理数集对加、减、乘、除法(除数不等于零)四则运算都封闭；D错：因为无理数集对加、减、乘、除法都不封闭．‎ 已知sinα＝，cosα＝，其中α是第二象限角，则m的值为________．‎ 解析：由＋＝1，‎ 整理得m2－‎8m＝0，∴m＝0或8.‎ ‎∵α是第二象限角，则sinα>0，cosα<0.‎ 经验证知m＝8.‎ 答案：8‎ 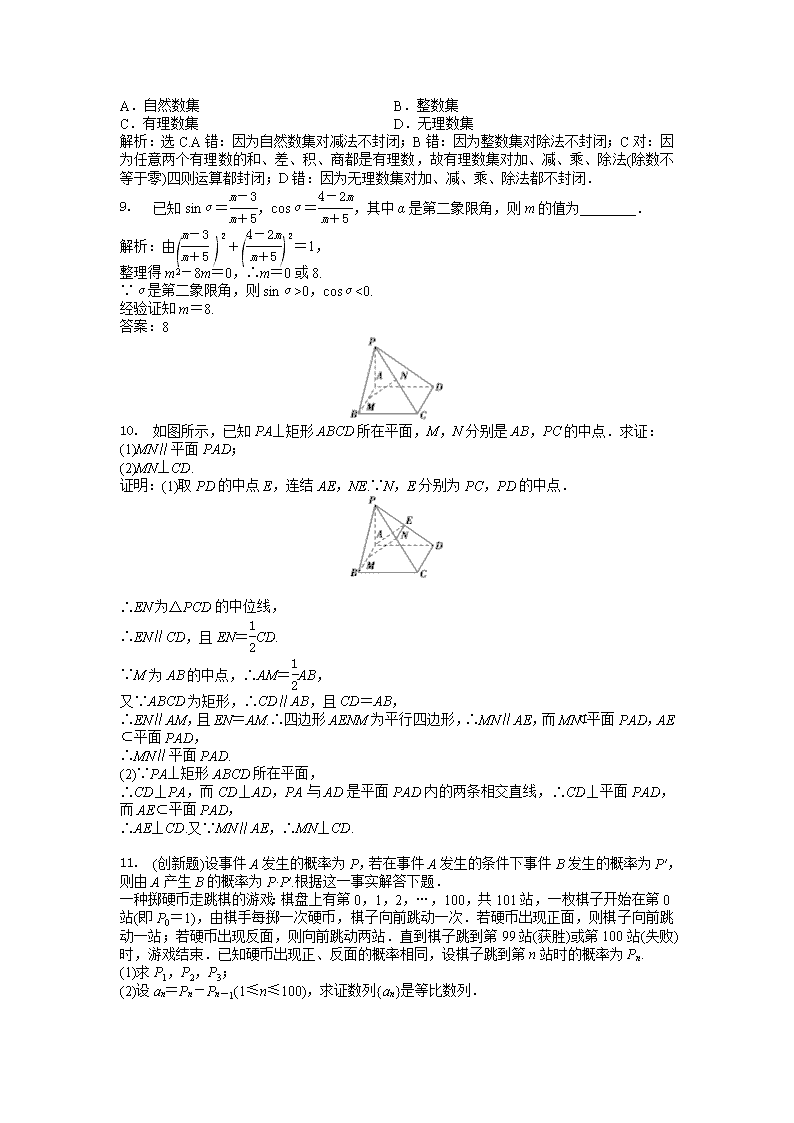如图所示，已知PA⊥矩形ABCD所在平面，M，N分别是AB，PC的中点．求证：‎ ‎(1)MN∥平面PAD；‎ ‎(2)MN⊥CD.‎ 证明：(1)取PD的中点E，连结AE，NE.∵N，E分别为PC，PD的中点．‎ ‎∴EN为△PCD的中位线，‎ ‎∴EN∥CD，且EN＝CD.‎ ‎∵M为AB的中点，∴AM＝AB，‎ 又∵ABCD为矩形，∴CD∥AB，且CD＝AB，‎ ‎∴EN∥AM，且EN＝AM.∴四边形AENM为平行四边形，∴MN∥AE，而MN⊄平面PAD，AE⊂平面PAD，‎ ‎∴MN∥平面PAD.‎ ‎(2)∵PA⊥矩形ABCD所在平面，‎ ‎∴CD⊥PA，而CD⊥AD，PA与AD是平面PAD内的两条相交直线，∴CD⊥平面PAD，而AE⊂平面PAD，‎ ‎∴AE⊥CD.又∵MN∥AE，∴MN⊥CD.‎ (创新题)设事件A发生的概率为P，若在事件A发生的条件下事件B发生的概率为P′，则由A产生B的概率为P·P′.根据这一事实解答下题．‎ 一种掷硬币走跳棋的游戏：棋盘上有第0，1，2，…，100，共101站，一枚棋子开始在第0站(即P0＝1)，由棋手每掷一次硬币，棋子向前跳动一次．若硬币出现正面，则棋子向前跳动一站；若硬币出现反面，则向前跳动两站．直到棋子跳到第99站(获胜)或第100站(失败)时，游戏结束．已知硬币出现正、反面的概率相同，设棋子跳到第n站时的概率为Pn.‎ ‎(1)求P1，P2，P3；‎ ‎(2)设an＝Pn－Pn－1(1≤n≤100)，求证数列{an}是等比数列．‎ 解：(1)P0＝1，∴P1＝，P2＝×＋＝，P3＝×＋×＝.‎ ‎(2)证明：棋子跳到第n站，必是从第n－1站或第n－2站跳来的(2≤n≤100)，所以Pn＝Pn ‎－1＋Pn－2，∴Pn－Pn－1＝－Pn－1＋Pn－1＋Pn－2＝－(Pn－1－Pn－2)，∴an＝－an－1(2≤n≤100)，且a1＝P1－P0＝－.故{an}是公比为－，首项为－的等比数列(1≤n≤100)．‎