人教A版选修1-13-1空间向量及其运算第1课时（含答案）

人教A版选修1-13-1空间向量及其运算第1课时（含答案）

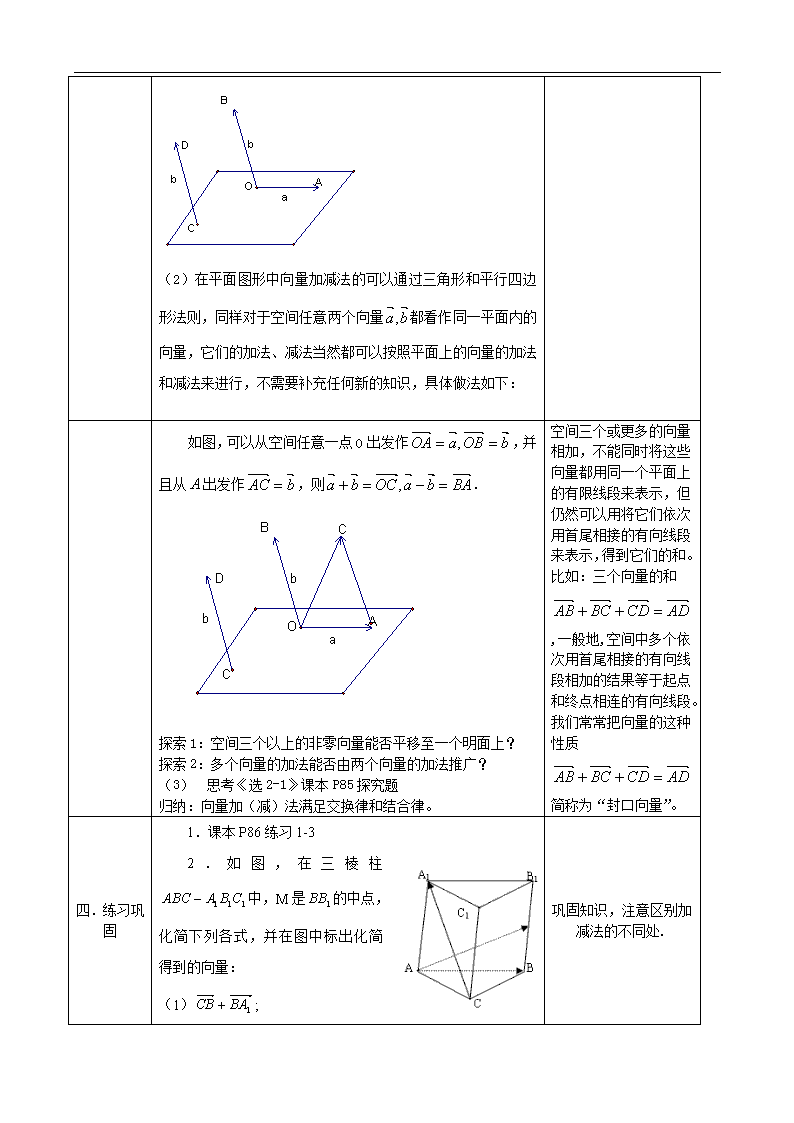
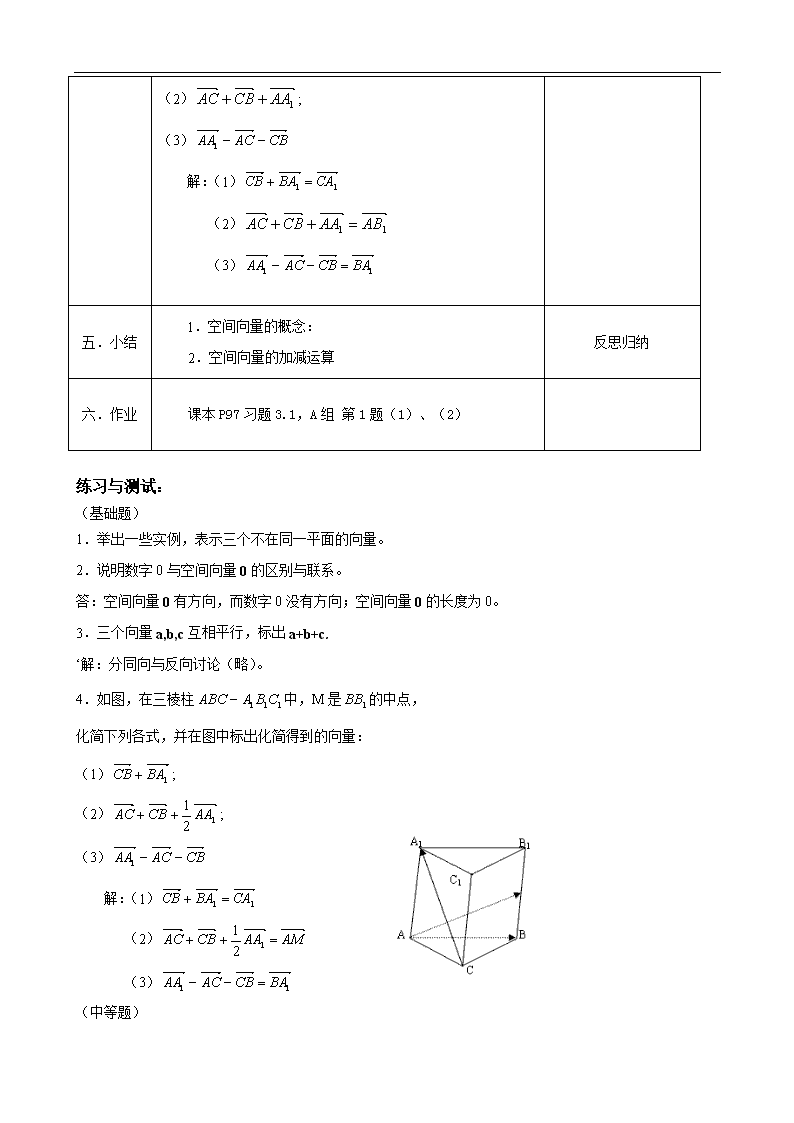
§3.1.1 空间向量及加减其运算 【学情分析】： 向量是一种重要的数学工具，它不仅在解决几何问题中有着广泛的应用，而且在物理学、工程科学等 方面也有着广泛的应用。在人教 A 版必修四中，读者已经认知了平面向量，现在，学习空间向量时要注意 与平面向量的类比，体会空间向量在解决立体几何问题中的作用。 【教学目标】： （1）知识与技能：理解和掌握空间向量的基本概念，向量的加减法 （2）过程与方法：通过高一学习的平面向量的知识，引申推广，理解和掌握向量的加减法 （3）情感态度与价值观：类比学习，注重类比、推广等思想方法的学习，运用向量的概念和运算解 决问题，培养学生的开拓创新能力。 【教学重点】： 空间向量的概念和加减运算 【教学难点】： 空间向量的应用 【教学过程设计】： 教学环节 教学活动 设计意图 一．情景引 入 （1） 一块均匀的正三角形的钢板所受重力为 500N，在它的 顶点处分别受力 F 1 ，F 2 ，F 3 ，每个力与同它相邻的三 角形的两边之间的夹角都是 60 o ，且| F 1 |=|F 2 |=|F 3 |=200N，这块钢板在这些力的作用下将 会怎样运动？这三个力至少多大时，才能提起这块钢 板？ （2） 八抬大轿中每个轿夫对轿子的支持力具有怎样的特 点？？ 从实际生活的例子出 发，使学生对不共面的 向量有一个更深刻的认 识。说明不同在一个平 面内的向量是随处可见 的。 二．新旧知 识比较 让我们将以前学过的向量的概念和运算回顾一下，看它们 是只限于平面上呢？还是本来就适用于空间中。 请学生自行阅读空间向量的相关概念：空间向量定义、模 长、零向量、单位向量、相反向量、相等向量。 请学生比较与平面向量的异同。 向量概念的关键词是大小和方向，所以它应既适用于平面 上的向量，也适合于空间中的向量，二者的区别仅仅在于：在 空间中比平面上有更多的不同的方向。因此平面几何中的向量 概念和知识就可以迁移到空间图形中。 （1）空间任意两个向量都可以平移到同一个平面内，成为同 一平面内的两个向量。 通过比较，既复习了平 面向量的基本概念，又 加强了对空间向量的认 识，注重类比学习，提 高学生举一反三的能 力。 三．类比推 广、探求新 知 如图，对于空间任何两个向量 ba, ，可以从空间任意一点 O 出发作 bOBaOA  , ，即用同一平面内的两条有向线段 OBOA, 来表示 ba, 让学生知道，数学中研 究的向量是自由向量， 与向量的起点无关，这 是数学中向量与物理中 矢量的最大区别。 b a b D B A O C （2）在平面图形中向量加减法的可以通过三角形和平行四边 形法则，同样对于空间任意两个向量 ba, 都看作同一平面内的 向量，它们的加法、减法当然都可以按照平面上的向量的加法 和减法来进行，不需要补充任何新的知识，具体做法如下： 如图，可以从空间任意一点 O 出发作 bOBaOA  , ，并 且从 A 出发作 bAC  ，则 BAbaOCba  , . b a b D B A C O C 探索 1：空间三个以上的非零向量能否平移至一个明面上？ 探索 2：多个向量的加法能否由两个向量的加法推广？ （3） 思考《选 2-1》课本 P85 探究题 归纳：向量加（减）法满足交换律和结合律。 空间三个或更多的向量 相加，不能同时将这些 向量都用同一个平面上 的有限线段来表示，但 仍然可以用将它们依次 用首尾相接的有向线段 来表示，得到它们的和。 比如：三个向量的和 ADCDBCAB  ,一般地,空间中多个依 次用首尾相接的有向线 段相加的结果等于起点 和终点相连的有向线 段。我们常常把向量的 这种性质 ADCDBCAB  简称为“封口向量”。 四．练习巩 固 1．课本 P86 练习 1-3 2．如图，在三棱柱 111 CBAABC  中，M 是 1BB 的中点， 化简下列各式，并在图中标出化简得 到的向量： （1） 1BACB  ; 巩固知识，注意区别加 减法的不同处. （2） 1AACBAC  ; （3） CBACAA 1 解：（1） 11 CABACB  （2） 11 ABAACBAC  （3） 11 BACBACAA  五．小结 1．空间向量的概念： 2．空间向量的加减运算 反思归纳 六．作业 课本 P97 习题 3.1，A 组 第 1 题（1）、（2） 练习与测试： （基础题） 1．举出一些实例，表示三个不在同一平面的向量。 2．说明数字 0 与空间向量 0 的区别与联系。 答：空间向量 0 有方向，而数字 0 没有方向；空间向量 0 的长度为 0。 3．三个向量 a,b,c 互相平行，标出 a+b+c. ‘解：分同向与反向讨论（略）。 4．如图，在三棱柱 111 CBAABC  中，M 是 1BB 的中点， 化简下列各式，并在图中标出化简得到的向量： （1） 1BACB  ; （2） 12 1 AACBAC  ; （3） CBACAA 1 解：（1） 11 CABACB  （2） AMAACBAC  12 1 （3） 11 BACBACAA  （中等题） 5．如图，在长方体 /// BDCAOADB  中， 3 , 4 , 2 ,OA i OB j OC k        ，点 E,F 分别是 //, BDDB 的中点， 试用向量 kji ,, 表示 OE 和OF 解： jiOE 42 3  kjiOF 242 3  。 6．在上题图中，试用向量 kji ,, 表示 EF 和 FE 解： EF = OEOF  = k2 ， FE =-- EF =-- k2