- 2021-07-01 发布 |
- 37.5 KB |
- 9页

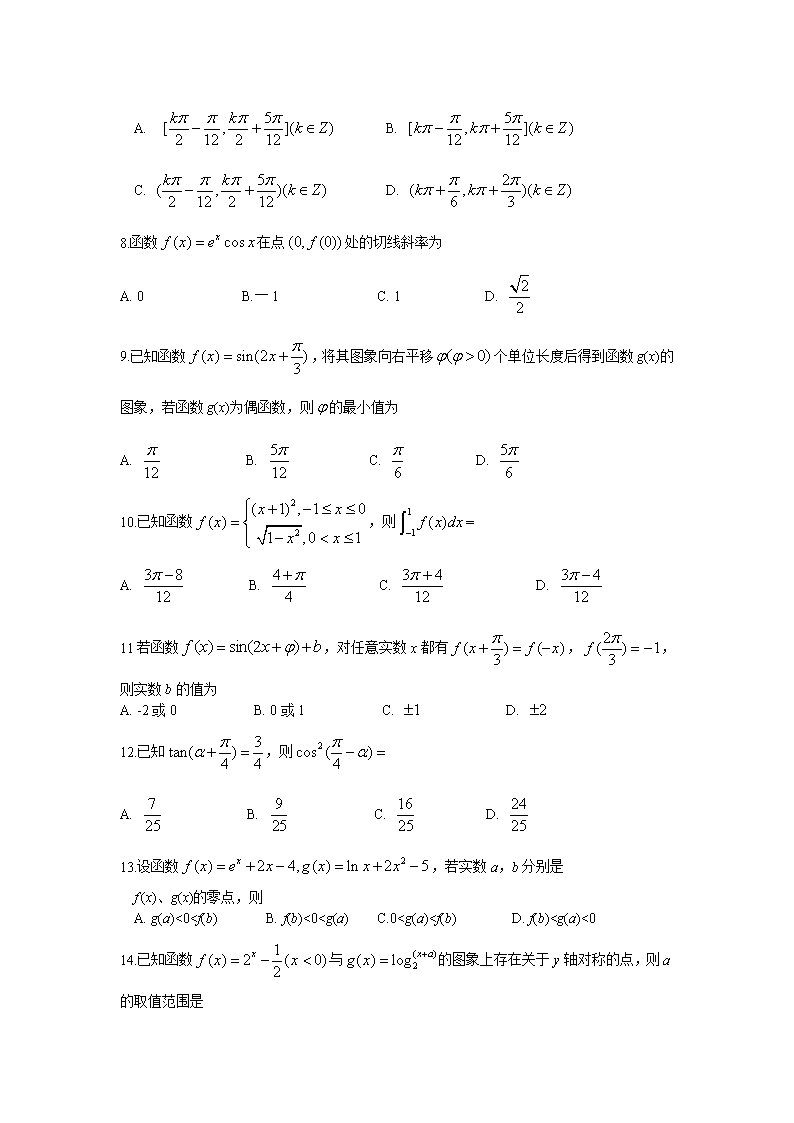

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年湖南省长郡中学高二下学期期末考试数学(理)试题 Word版
长郡中学2018-2019学年度高二第二学期期末考试 数学(理科) 时量:120分钟 满分:100分 一、选择题(每小题3分,共45分) 1.设集合A=.若{1}.则m= A.1 B. C. D.一1 ★2.已知函数y=f(x2-1)的定义域为[0.3],则函数y=f(x)的定义域为 A. B. [1.2] C. [0.3] D.[一1.8] 3.在平面直角坐标系xOy中.角与角均以Ox为始边.它们的终边关于y轴对称.若角是第三象限角,且,则 A. B. C. D. 4.已知命题“,使得”是真命题,则实数a的取 值范围是 A. B. C.(一1,3) D.(一3.1) 5.已知某批零件的长度误差(单位:毫米)服从正态分布N(1,32).从中随机 取一件.其长度误差落在区间(4,7)内的概率为 (附:若随机变量服从正态分布N,则68.26%,95.44%) A. 4. 56% B. 13.59% C. 27. 18% D. 31. 74% 6.定义在R上的奇函数f(x)满足f (x-2)=f(x+2),且当时,,则f(9)= A. B. 2 C. D. ★7.函数的单调递增区间为 A. B. C. D. 8.函数在点处的切线斜率为 A. 0 B.一1 C. 1 D. 9.已知函数,将其图象向右平移个单位长度后得到函数g(x)的图象,若函数g(x)为偶函数,则的最小值为 A. B. C. D. 10.已知函数,则= A. B. C. D. 11若函数,对任意实数x都有,,则实数b的值为 A. -2或0 B. 0或1 C. D. 12.已知,则 A. B. C. D. 13.设函数,若实数a,b分别是 f (x)、g(x)的零点,则 A. g(a)<0查看更多