【数学】重庆市忠县三汇中学2019-2020学年高一上学期期中考试试题 （解析版）

【数学】重庆市忠县三汇中学2019-2020学年高一上学期期中考试试题 （解析版）

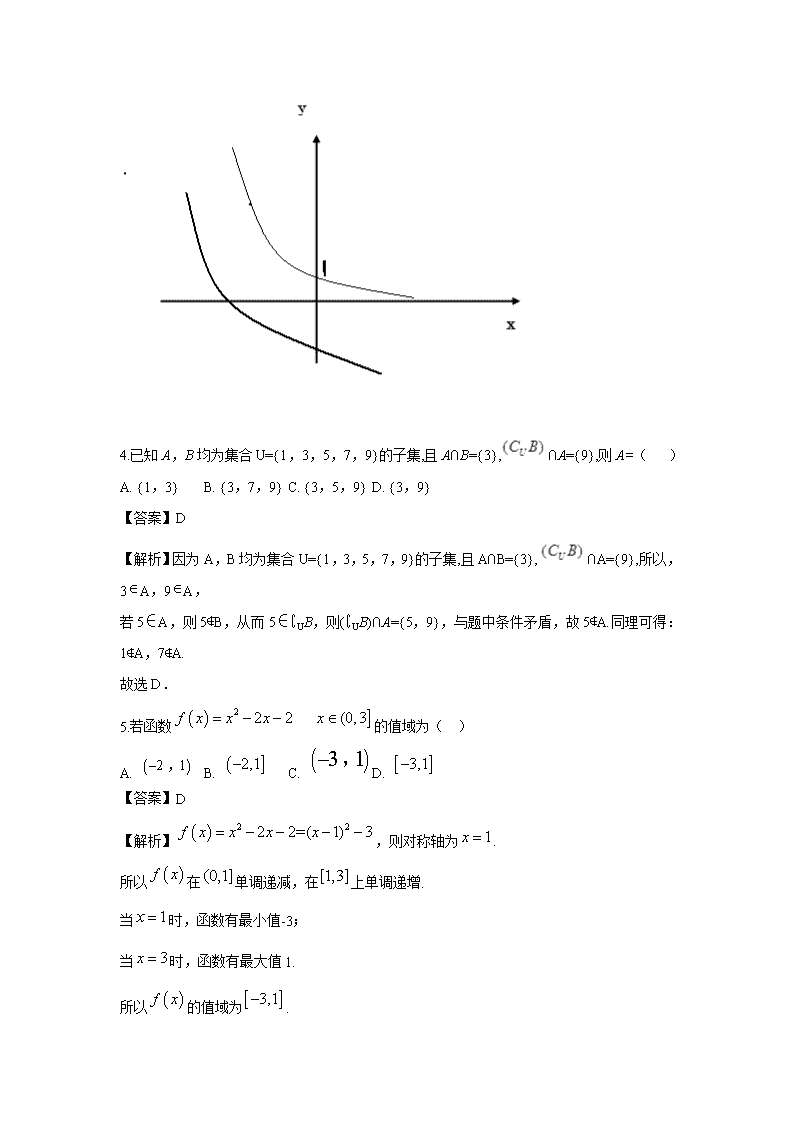
www.ks5u.com 重庆市忠县三汇中学2019-2020学年高一上学期期中考试 数学试题 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知，，则下列关系不正确的是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】对A, ，,显然，所以A正确.‎ 对B, ,显然,所以B不正确.‎ 对C, 由，，显然,所以C正确.‎ 对D, 由，，显然 成立，所以D正确.‎ 故选：B.‎ ‎2.设集合，集合，则（ ）．‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】,故选B．‎ ‎3.已知,则函数的图像必定不经过（ ）‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎【答案】A ‎【解析】此题考查指数函数的图像的性质和指数函数的上下平移；有已知得到：此指数函数是减函数，分布在第一，二象限，渐近线是轴，即；（）是由指数函数向下平移大于1个单位得到的，即原来指数函数所过的定点向下平移到原点的下方了，所以图像不经过第一象限，所以选A，如下图所示：‎ ‎4.已知A，B均为集合U={1，3，5，7，9}的子集,且A∩B={3},∩A={9},则A=（ 　）‎ A. {1，3} B. {3，7，9} C. {3，5，9} D. {3，9}‎ ‎【答案】D ‎【解析】因为A，B均为集合U={1，3，5，7，9}的子集,且A∩B={3},∩A={9},所以，3A，9A，‎ 若5∈A，则5∉B，从而5∈∁UB，则(∁UB)∩A={5，9}，与题中条件矛盾，故5∉A.同理可得：1∉A，7∉A.‎ 故选D．‎ ‎5.若函数的值域为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】，则对称轴为.‎ 所以在单调递减，在上单调递增.‎ 当时，函数有最小值-3；‎ 当时，函数有最大值1.‎ 所以的值域为. ‎ 故选：D.‎ ‎6.函数的定义域是（   ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】∵函数f（x）=+lg（3x+1），∴；解得﹣＜x＜1，‎ ‎∴函数f（x）定义域是（﹣，1）．‎ 故选B．‎ ‎7.函数的单调减区间为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】设，则由.‎ 得到，即函数的定义域.‎ 又.‎ 所以在上单调递减,‎ 即函数在上单调递减.‎ 故选：B.‎ ‎8.己知是定义在上的奇函数，当时，，那么不等式的解集是( )‎ A. B. 或 C. D. 或 ‎【答案】B ‎【解析】当时，‎ ‎ ‎ ‎ 是定义在R上的奇函数，‎ 又，则 ‎（1）当时， ，解得 ‎（2）当时，，恒成立 ‎（3）当时，，解得 综上所述，则的解集为或 故答案为B ‎9.若关于x的方程有两个不等实根，则的取值范围是 （）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】当a＞1时，两个函数的图象如下：‎ 当0＜a＜1时，两个函数的图象如下：‎ 据题意，函数的图象与直线有两个不同的交点.由图可知，，所以，故选D.‎ ‎10.函数是偶函数，则函数的对称轴是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】.‎ 因为函数是偶函数.‎ 所以其图像关于轴对称.‎ 又函数的图像是由函数的图像向左平移个单位得到的.‎ 所以函数的对称轴是.‎ 故选：D.‎ ‎11.已知集合, .且，则实数m的取值范围为 (       )‎ A. [-1，2) B. [-1，3] C. [-2，+∞ D. [-1，+∞ ‎ ‎【答案】D ‎【解析】由,得.即.‎ 由,即.‎ 当时，满足条件,则解得.‎ 当时，要使得，则.‎ 解得：.‎ 综上满足条件的 的范围是：.‎ 故选：D.‎ ‎12.已知满足对任意都成立，那么的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】对任意都有成立.‎ 则在R上为减函数.‎ 当 时，为减函数，则, 即.‎ 当 时，为减函数，则.‎ 要使得在上为减函数，则在处有:.即.‎ 所以的取值范围是：.‎ 故选：D.‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13._____________‎ ‎【答案】‎ ‎【解析】.‎ 故答案为：.‎ ‎14.若，则满足条件的集合A有______个.‎ ‎【答案】7‎ ‎【解析】由,则中必含有元素1, 2.‎ 对于元素3,4,5可以没有，可以有一个，可以有两个，但不能都在集合中.‎ 所以满足条件的有：，，，，,‎ ‎,共7个.‎ 故答案为：7.‎ ‎15.已知 50名学生做的物理、化学两种实验，已知物理实验做得正确得有40人，化学实验做得正确得有31人，两种实验都做错得有4人，则这两种实验都做对的有 人.‎ ‎【答案】25‎ ‎【解析】根据题意可设,,并将两种实验都做对的学生记为人,则可用文氏图将其关系表示如下:‎ 结合文氏图及题意知:,解之得:,故两种实验都做对的学生为25人.‎ ‎16.给出下列命题：‎ 函数与函数的定义域相同；‎ ‎②函数与的值域相同；‎ ‎③函数与函数均是奇函数；‎ ‎④函数与在上都是增函数。‎ 其中正确命题的序号是_______________‎ ‎【答案】①③‎ ‎【解析】对①. 函数的定义域为,函数的定义域为R,所以①正确.‎ 对②. 函数的值域为,的值域为，所以②不正确.‎ 对③. 设，则，‎ 则，所以为奇函数. ‎ 设，因为为偶函数，‎ 则为奇函数, 所以③正确.‎ 对④. 函数在上单调递减，所以④不正确.‎ 故答案为：①③.‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17.（1）已知，计算的值.‎ ‎（2）计算的值.‎ 解： (1) 由=.‎ ‎(2) =.‎ ‎=.‎ ‎18.已知 ‎(1)作出的图像,并写出单调区间;‎ ‎(2)解不等式.‎ 解： (1)由，则图像如下:‎ 由函数的图像有，在上单调递减，在上单调递增.‎ ‎(2) ,即，即.‎ 可解得：.‎ 所以不等式的解集为：.‎ ‎19.已知，.‎ ‎（1）求；‎ ‎（2）求且.‎ 解：由，即.‎ 所以,即.则或.‎ 所以, 或.‎ ‎(1) ,则 = .‎ ‎(2) 且表示元素在集合中而不在集合中.‎ 且=.‎ ‎20.已知集合，，. ‎ ‎（1）求；‎ ‎（2）若，求实数的取值范围.‎ 解（1）由题意：‎ ‎，∴‎ ‎∴. ‎ ‎（2）∵，∴‎ ‎∵‎ ‎∴ ∴‎ ‎21.已知函数 ，.‎ ‎(1)求的值；‎ ‎(2)试判断并证明函数的奇偶性；‎ ‎(3)试判断并证明函数在区间上的单调性并求的值域．‎ 解：(1)因为所以;‎ ‎(2)由（1）知的定义域为，因为 所以为偶函数；‎ ‎（3）对任意，则 =‎ ‎=，则所以在区间上为增函数，‎ 又为偶函数，所以在区间上是减函数，所以的最小值为=2 ,‎ 所以值域为.‎ ‎22.已知函数（）满足：，当时，，且；‎ ‎（1）证明：是定义域上的减函数；‎ ‎（2）解不等式 解：(1)任取且设.‎ 则 ‎.‎ 因为，则.‎ 又当时，. 则.‎ 所以,即.‎ 所以是定义域上的减函数.‎ ‎(2)由，可得.‎ 不等式化为.‎ 即,由（1）可知是定义域上的减函数.‎ 所以,解得.‎ 所以不等式的解集为.‎