2019-2020学年黑龙江省大庆市第四中学高一上学期第二次月考数学（文）试题

2019-2020学年黑龙江省大庆市第四中学高一上学期第二次月考数学（文）试题

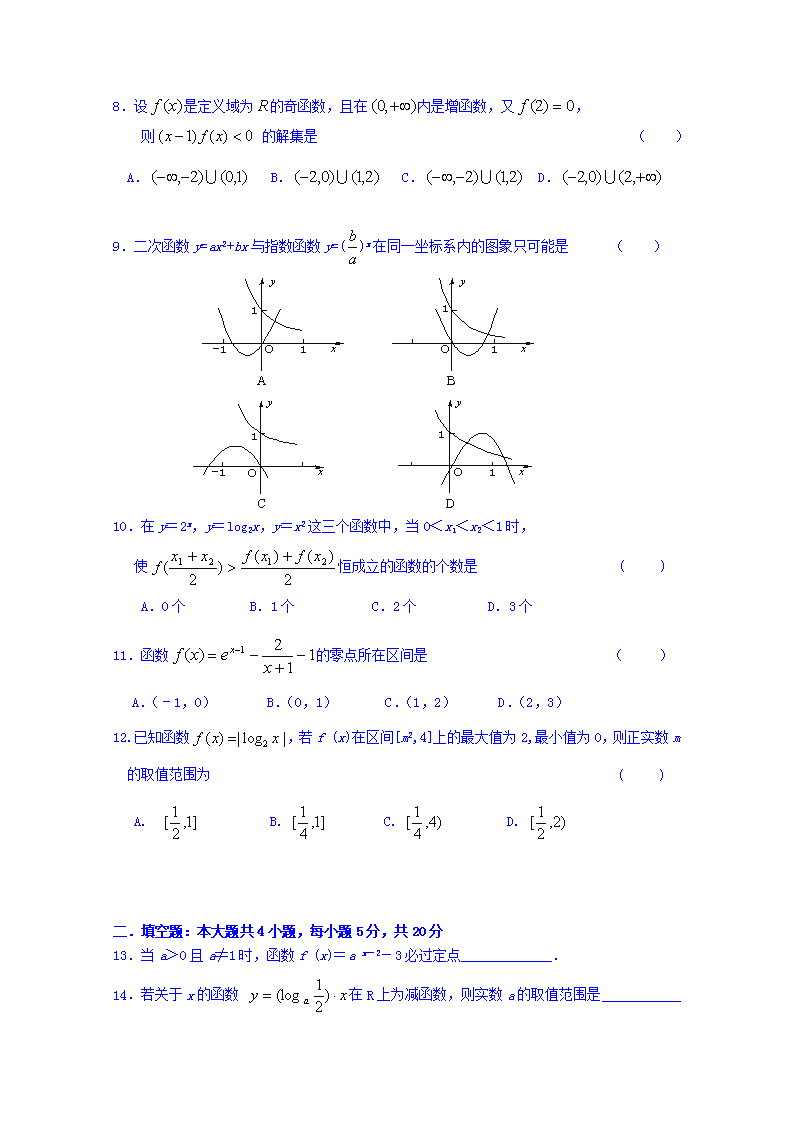
大庆四中2019～2020学年度第一学期第二次检测高一年级 数学（文科）试题 考试时间：120分钟 分值：150分 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分 第Ⅰ卷（选择题）‎ 一、选择题。本卷共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.已知全集,集合,,则为 （ ）‎ ‎ A. B. C. D. ‎ ‎2．下列函数中，在区间(0,1)上为增函数的是 (　 　)‎ A．y＝2x2－x＋3 B． C． D．‎ ‎3.已知函数，则 （ ）‎ A． B. C. D. ‎ ‎4. 已知, ,, 则 ( )‎ ‎ A. a>b>c B. a>c>b C. b>a>c D. c>a>b ‎5．若，则函数 f (x)的定义域为 (　 　) ‎ A. B．(0，＋∞) C. D. ‎6．与函数y＝有相同图象的一个函数是 (　　 )‎ A．y＝－x B．y＝x C．y＝－ D．y＝x2 ‎7．给出下列说法正确的是 ( ) ‎ A. 函数y＝f(x)，x∈R的图象与直线x＝a可能有两个不同的交点；‎ B. 函数与函数是相等函数；‎ C. 对于函数y＝f(x)，x∈[a，b]，若有f(a)·f(b)＜0，则f(x)在(a，b)内有零点；‎ D. 对于指数函数y＝2x与幂函数y＝x2，总存在x0，当x＞x0时，有2x＞x2成立；‎ ‎8．设是定义域为的奇函数，且在内是增函数，又，‎ ‎ 则 的解集是 （ ）‎ A． B． C． D．‎ ‎9．二次函数y=ax2+bx与指数函数y=()x在同一坐标系内的图象只可能是 （ ）‎ ‎ ‎ ‎10．在y＝2x，y＝log2x，y＝x2这三个函数中，当0＜x1＜x2＜1时，‎ ‎ 使恒成立的函数的个数是 (　 　)‎ A．0个 B．1个 C．2个 D．3个 ‎11．函数的零点所在区间是 （　 　）‎ A．（﹣1，0） B．（0，1） C．（1，2） D．（2，3）‎ ‎12.已知函数，若f (x)在区间[m2,4]上的最大值为2,最小值为0，则正实数m的取值范围为 ( )‎ A. B. C. D. ‎ 二．填空题：本大题共4小题，每小题5分，共20分 ‎13．当a＞0且a≠1时，函数f (x)＝a x－2－3必过定点_____________．‎ ‎14．若关于x的函数 在R上为减函数，则实数a的取值范围是 ‎ ‎15．若函数y＝loga(x2－ax＋1)无最小值，则实数a的取值范围是___________‎ ‎16．已知函数f(x)＝若关于x的方程f(x)＝k有两个不同的实根，‎ 则实数k的取值范围是________．‎ 三.解答题:本大题共6小题,共70分 . 解答应写出文字说明,证明过程或演算步骤 ‎17. （本小题满分10分）‎ 若集合，且，求实数的值.‎ ‎18．（本小题满分12分）‎ 已知幂函数f(x)的图象过点(，2)，幂函数g(x)的图象过点.‎ ‎（Ⅰ）求f(x)，g(x)的解析式； （Ⅱ）解关于x的不等式 ‎3f(x)>‎2g(x)+1；‎ ‎19. （本小题满分12分）‎ 已知函数f（x）＝（a2﹣‎2a﹣2）ax是指数函数．‎ ‎（Ⅰ）求实数a的值；并求出关于x的不等式：loga（1+x）＜loga（2﹣x）的解集.‎ ‎（Ⅱ）判断的奇偶性，并加以证明.‎ ‎20．（本小题满分12分） 已知函数f（x）＝2|x+1|﹣|x﹣1|．‎ ‎（Ⅰ）在图中作出函数y＝f（x）的图象，并求出其与直线y＝1围成的封闭图形的面积；‎ ‎（Ⅱ）解关于x的不等式：f（x）≥3 ‎ ‎21．（本小题满分12分）‎ 已知函数f (x)是定义在R上的奇函数， 当时，‎ ‎（Ⅰ）求函数f (x)的解析式；并写出函数的单调区间 ‎（Ⅱ）函数f (x)在区间[-3,a]上的最小值为g(a), 求g(a)的值域.‎ ‎22. （本小题满分12分）‎ 已知，当时，恒有.‎ ‎（Ⅰ）求的解析式；‎ ‎（Ⅱ）若方程的解集是空集，求实数的取值范围.‎ 大庆四中2019～2020学年度第一学期第二次检测高一年级 数学（文科）试题答案 答案：DCABC ADBAB CA ‎13.(2,-2) 14. a>1 15. 16. (1,2) ‎ ‎17.解：①当a=0时，N=Φ, 满足 （3分）‎ ‎②当a≠0时,M={-3，2}，N={}，要使，则=-3或=2，解得：‎ ‎ a=-或a= （6分）综上，满足题意的a的值为：0，,-， （10分）‎ ‎18.解：(1)设f(x)＝xα，∵其图象过点(，2)，故2＝()α，‎ 解得a＝2，∴f(x)＝x2.设g(x)＝xβ，‎ ‎∵其图象过点，∴＝2β，解得β＝－2， ∴g(x)＝x－2.‎ ‎(2) 3 x2>2 x－2+1, 3 x4- x2-2>0, (3 x2+2)( x2-1)>0 解得：x<-1或x>1‎ ‎19. (1) 解：a2‎-2a-2=1, 解得a=3或a=-1(舍)‎ 不等式：loga（1+x）＜loga（2﹣x）即log3（1+x）＜log3（2﹣x）．‎ 可化为：2﹣x＞1+x＞0， ∴﹣1＜x＜，‎ 即不等式：loga（1+x）＜loga（2﹣x）的解集为{x|﹣1＜x＜}．‎ ‎ (2) =,‎ ‎ 所以，函数为奇函数 ‎20.‎ ‎（Ⅰ）函数f（x）＝2|x+1|﹣|x﹣1|＝‎ ‎，‎ 如图所示 利用﹣x﹣3＝1，解得x＝﹣4，所以AC＝4，AC边上的高为2+1＝3，‎ 所以m＝．‎ f（x）≥3 解得 解集为：‎ ‎21. 解：（1）设时，-x>0, ,‎ ‎ 。因为 所以，函数 单调增区间为： 单调减区间为 （-2,2）‎ ‎(2) 当-3

查看更多