高中数学必修1教案：第五章（第3课时）向量的加法与减法（2）

高中数学必修1教案：第五章（第3课时）向量的加法与减法（2）

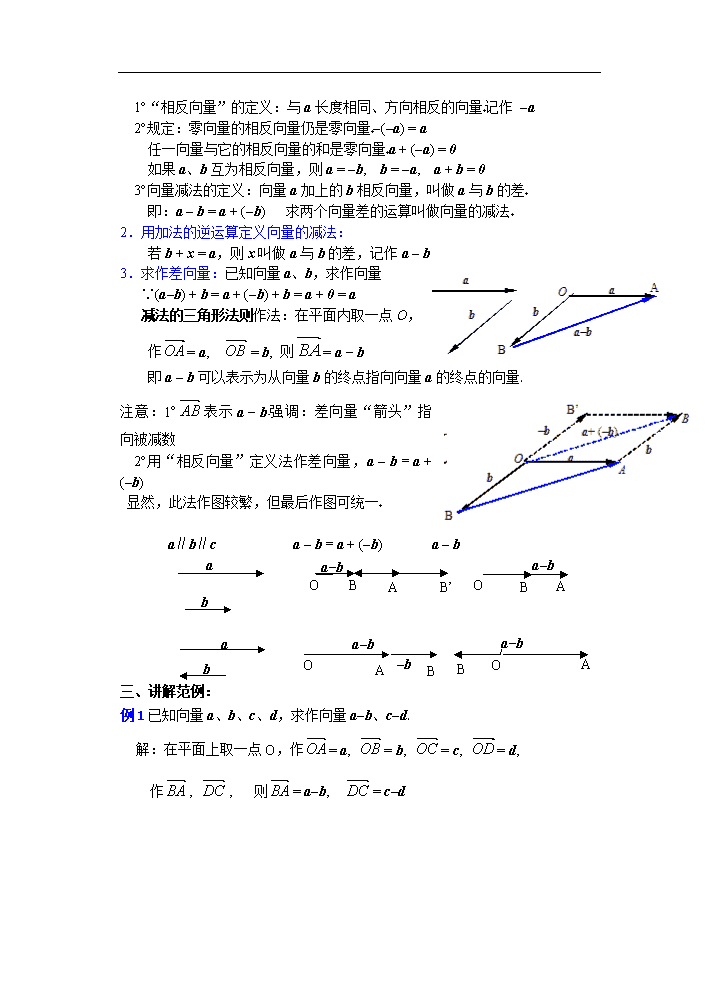
课 题：向量的加法与减法（2）‎ 教学目的：‎ ‎⑴了解相反向量的概念；‎ ‎⑵掌握向量的减法，会作两个向量的减向量 教学重点：向量减法的概念和向量减法的作图.‎ 教学难点：对向量减法定义的理解 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程：‎ 一、复习引入：‎ ‎1.向量的概念：既有大小又有方向的量叫向量,有二个要素：大小、方向.‎ ‎2.向量的表示方法：①用有向线段表示；②用字母ａ、ｂ等表示；‎ ‎③用有向线段的起点与终点字母：；‎ ‎④向量的大小――长度称为向量的模，记作||. ‎ ‎3.零向量、单位向量概念：‎ ‎①长度为0的向量叫零向量，记作的方向是任意的 ‎②长度为1个单位长度的向量，叫单位向量.零向量、单位向量的定义都是只限制大小，不确定方向.‎ ‎4.平行向量定义：‎ ‎①方向相同或相反的非零向量叫平行向量；‎ ‎②我们规定0与任一向量平行.向量ａ、ｂ、ｃ平行，记作ａ∥ｂ∥ｃ.‎ ‎5.相等向量定义：长度相等且方向相同的向量叫相等向量.‎ ‎6.共线向量与平行向量关系：平行向量就是共线向量.‎ ‎7.向量的加法：求两个向量和的运算，叫做向量的加法 几何中向量加法是用几何作图来定义的，一般有两种方法，即向量加法的三角形法则（“首尾相接，首尾连”）和平行四边形法则（对于两个向量共线不适应）‎ ‎8．向量加法的交换律：+=+‎ ‎9．向量加法的结合律：(+) +=+ (+)‎ 二、讲解新课：向量的减法 ‎1．用“相反向量”定义向量的减法：‎ ‎1°“相反向量”的定义：与a长度相同、方向相反的向量记作 -a ‎2°规定：零向量的相反向量仍是零向量-(-a) = a 任一向量与它的相反向量的和是零向量a + (-a) = 0‎ 如果a、b互为相反向量，则a = -b, b = -a, a + b = 0‎ ‎3°向量减法的定义：向量a加上的b相反向量，叫做a与b的差 即：a - b = a + (-b) 求两个向量差的运算叫做向量的减法 ‎2．用加法的逆运算定义向量的减法：‎ 若b + x = a，则x叫做a与b的差，记作a - b ‎3．求作差向量：已知向量a、b，求作向量 ‎ ∵(a-b) + b = a + (-b) + b = a + 0 = a ‎ 减法的三角形法则作法：在平面内取一点O，‎ ‎ 作= a, = b, 则= a - b ‎ 即a - b可以表示为从向量b的终点指向向量a的终点的向量 注意：1°表示a - b强调：差向量“箭头”指向被减数 ‎ 2°用“相反向量”定义法作差向量，a - b = a + (-b)‎ ‎ 显然，此法作图较繁，但最后作图可统一 a-b A A B B B’‎ O a-b a a b b O A O B a-b a-b B A O -b a∥b∥c a - b = a + (-b) a - b 三、讲解范例：‎ 例1已知向量a、b、c、d，求作向量a-b、c-d 解：在平面上取一点O，作= a, = b, = c, = d, ‎ ‎ 作, , 则= a-b, = c-d 例2平行四边形中，，，用，表示向量、‎ 解：由平行四边形法则得：‎ ‎= a + b, = = a-b 变式一：当a, b满足什么条件时，a+b与a-b垂直？（|a| = |b|）‎ 变式二：当a, b满足什么条件时，|a+b| = |a-b|？（a, b互相垂直）‎ 变式三：a+b与a-b可能是相当向量吗？（不可能，∵对角线方向不同）‎ 四、课堂练习：‎ ‎1.下列等式:①a+0=a ②b+a=a+b ③-(-a)=a ④a+(-a)=0 ⑤a+(-b)=a-b正确的个数是( ) A.2 B.3 C.4 D.5‎ ‎2.下列等式中一定能成立的是( ) A. += B. -=‎ C.+= D. -=‎ ‎3.化简-++的结果等于( ) A. B. C.  D. ‎ ‎4.已知=a, =b,若||=12,||=5,且∠AOB=90°,则|a-b|= .‎ ‎5.在正六边形ABCDEF中, =m, =n,则= .‎ ‎6.已知a、b是非零向量,则|a-b|=|a|+|b|时,应满足条件 . 参考答案：1.C 2.D 3.B 4. 135.m-n 6.a与b反向 五、小结 向量减法的定义、作图法 六、课后作业：‎ ‎1.在△ABC中, =a, =b,则等于( ) A.a+b B.-a+(-b) C.a-b D.b-a ‎2.O为平行四边形ABCD平面上的点,设=a, =b, =c, =d,则 A.a+b+c+d=0 B.a-b+c-d=0 C.a+b-c-d=0 D.a-b-c+d=0‎ ‎3.在下列各题中,正确的命题个数为( ) ‎(1)若向量a与b方向相反,且|a|＞|b|,则a+b与a方向相同 ‎(2)若向量a与b方向相反,且|a|＞|b|,则a-b与a+b方向相同 ‎(3)若向量a与b方向相同,且|a|＜|b|,则a-b与a方向相反 ‎(4)若向量a与b方向相同,且|a|＜|b|,则a-b与a+b方向相反 A.1 B.2 C.3 D.4 ‎4.如图，在四边形ABCD中,根据图示填空: a+b= ,b+c= ,c-d= ,a+b+c-d= . ‎5.一艘船从A点出发以2km/h的速度向垂直于对岸的方向行驶,而船实际行驶速度的大小为4 km/h,则河水的流速的大小为 .‎ ‎6.若a、b共线且|a+b|＜|a-b|成立,则a与b的关系为 .‎ ‎7.在五边形ABCDE中,设=a, =b, =c, =d,用a、b、c、d表示.‎ ‎8.如图所示，O是四边形ABCD内任一点，试根据图中给出的向量，确定a、b、c、d的方向（用箭头表示）,使a+b=,c-d=,并画出b-c和a+d. ‎ ‎9.已知O是□ABCD的对角线AC与BD的交点,若=a, =b, =c,试证明:c+a-b=.‎ 参考答案：1.B 2.B 3.D 4.-f -e f 0 ‎5.2 km/h 6.a与b的方向相反且都不为零向量 7.b+d-a-c ‎8. ‎9.(略) 七、板书设计（略）‎ 八、课后记： ‎