山东省学业水平考试数学模拟试题01

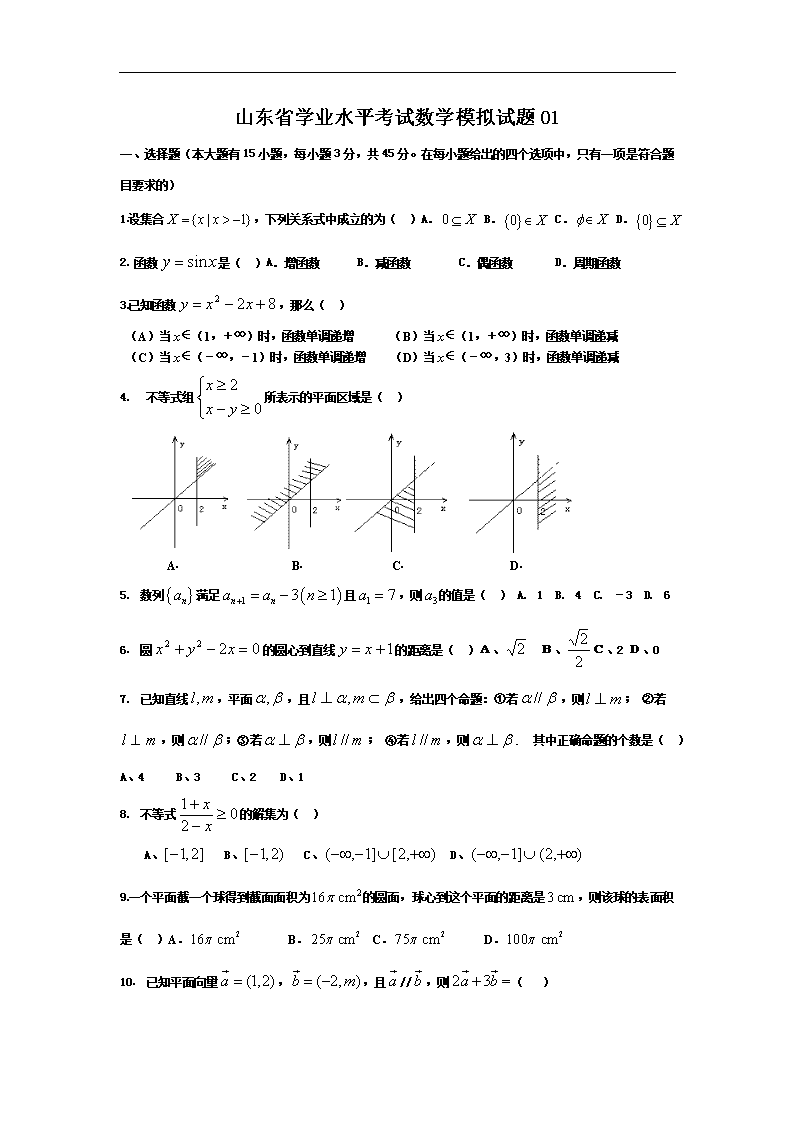
山东省学业水平考试数学模拟试题01

山东省学业水平考试数学模拟试题01‎ 一、选择题（本大题有15小题，每小题3分，共45分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1设集合，下列关系式中成立的为（ ）A． B． C． D．‎ ‎2 函数是（ ）A．增函数 B．减函数 C．偶函数 D．周期函数 ‎3已知函数，那么（ ）‎ ‎ （A）当x∈（1，＋∞）时，函数单调递增 （B）当x∈（1，＋∞）时，函数单调递减 ‎ （C）当x∈（－∞，－1）时，函数单调递增 （D）当x∈（－∞，3）时，函数单调递减 ‎4 不等式组所表示的平面区域是（ ）‎ ‎ ‎ A B C D ‎5 数列满足且，则的值是（ ） A 1 B 4 C －3 D 6‎ ‎6 圆的圆心到直线的距离是（ ）Ａ、　Ｂ、Ｃ、2 Ｄ、0‎ ‎7 已知直线，平面，且，给出四个命题：①若，则； ②若，则；③若，则； ④若，则. 其中正确命题的个数是（ ）A、4 B、‎3 ‎ C、2 D、1‎ ‎8 不等式的解集为（ ）‎ A、 B、 C、 D、‎ ‎9一个平面截一个球得到截面面积为的圆面，球心到这个平面的距离是，则该球的表面积是（　）A． B． C． D．‎ ‎10 已知平面向量，，且//，则＝（ ）‎ A． B． C． D．‎ 开始 K=2‎ P=0‎ P<20？‎ P=p+k K=k+2‎ 输出k 结束 是 否 ‎11 直线将圆平分，且在两坐标轴上的截距 相等，则直线的方程是（ ）‎ A. B.‎ C. D.‎ ‎12若执行下面的程序图的算法，则输出的k的值为（ ）．‎ ‎ 　A．8　　　 B．‎9　‎　　　C．10　　　　D．11‎ ‎13 若，（ ）‎ A. 第二象限 B.第三象限 C.第四象限 D . 第三、四象限 ‎14若是正实数，则（ ）A. B. C. D.‎ ‎15 设为等差数列的前n项的和，，，则的值为（ ）‎ A、 B、 C、2007 D、2008‎ 二、填空题（本大题有5小题，每小题3分，共15分。把答案填在题中的横线上）‎ ‎16．某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为2：3：5，现用分层抽 样方法抽出一个容量为n的样本，其中A种型号产品有16件，那么此样本的容量n= ‎ B ‎17 设函数，若，则实数a的取值范围是 ‎ ‎18 如果sin＝，那么cos的值是_________‎ ‎19 有5把钥匙，其中有2把能打开锁，现从中任取1把能打开锁的概率是 ‎ ‎20．如图，已知两个灯塔A和B与观察站C的距离都为，灯塔A在观察站 C的北偏东，灯塔B在观察站C的南偏东，则灯塔A,B间的距离是 ‎ 一、选择题答题卡：班级：_______姓名：___________考号：_______‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答案 二、填空题答题卡： 16、_________17、_________18、__________ 19、__________20、__________‎ 三、解答题（本大题有5小题，共40分。解答应写出文字说明，证明过程或演算步骤）‎ ‎21．（本小题满分8分）试证明函数在上为增函数．‎ ‎22．（本小题满分8分）设等差数列的前项和为, 已知.‎ ‎ （Ⅰ）求首项和公差的值; （Ⅱ）若，求的值.‎ ‎23　（本小题满分8分）求圆心在直线4 x + y = 0上，并过点P（4，1），Q（2，－1）的圆的方程 ‎24．已知，.‎ ‎(1)若求的值;（2）设求的最小值。‎ ‎25 （本小题满分8分）如图，直三棱柱中，，，， M是A1B1的中点 ‎ ‎（1） 求证C‎1M^平面；‎ ‎（2） 求异面直线与所成角的余弦值 ‎ 山东省学业水平考试数学模拟试题01参考答案与评分标准 一、选择题1．D 2．D 3．A 4．D 5．A 6．A 7．C8．B9．D 10．B 11．C 12．C 13．C 14．C 15．B 二、填空题 16．80 17． 18． 19． 20．‎ 三、解答题（本大题有5小题，满分40分。解答应写出文字说明，证明过程或演算步骤）‎ ‎21解：证明：设是上的任意两个实数，且，则 ‎．，，，，即．故函数在上为增函数．‎ ‎22. 解: (Ⅰ) ,‎ 解得 (Ⅱ)由,得, 解得或(舍去).. ‎ ‎23 解：解:∵点P，Q在圆上，∴圆心在PQ的垂直平分线上，PQ的垂直平分线的方程为x + y －3 = 0 ‎ 又圆心在直线 4 x + y = 0上，∴它们的交点为圆心 ‎ 由 即圆心坐标为(－1，4)，半径, ‎ 因此所求圆的方程为 ‎24 (1)∵∴，而 ‎=‎ ‎ ‎ ‎25 (1)∵直三棱柱，∴　，　∴， ∵， M是A1B1的中点，∴ 又　　∴ C‎1M^平面 ‎ ‎(2)设、的中点分别为、，　连接，∴∥，连接，∴∥，‎ ‎∴是异面直线与所成角或其补角；设点是的中点，连接、，在Rt△，在△中，，，‎ ‎∴ ‎ ‎∴异面直线与所成角的余弦值为 ‎