2018-2019学年山西大学附属中学高二下学期5月模块诊断 数学(文) word版
山西大学附中
2018~2019 学年高二第二学期 5 月(总第四次)模块诊断
数学试题(文科)
考试时间:120 分钟 满分:150 分
一. 选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,
只有一个是符合题目要求的.)
1.复数 的虚部为( )
A. B. C.2 D.-2
2.下面几种推理过程是演绎推理的是( )
A.某校高二 8 个班,1 班有 51 人,2 班有 53 人,3 班有 52 人,由此推测各班人数都超过 50
人
B.由三角形的性质,推测空间四面体的性质
C.平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D.在数列 中, , ,由此归纳出 的通项公式
3.点 的直角坐标为 ,则点푃的极坐标可以为( )
A. B. C.
D.
4.在建立两个变量 与 的回归模型中,分别选择了 4 个不同的模型,结合它们的相关指
数 判断,其中拟合效果最好的为( )
A. 模型 1 的相关指数 为 0.85 B. 模型 2 的相关指数 为 0.25
C. 模型 3 的相关指数 为 0.7 D. 模型 4 的相关指数 为 0.3
5.已知函数 在区间 上是减函数,则实数 的取值范围是
( )
A. B. C. D.
6.在极坐标系中,点 到直线 的距离是( )
A. B. C. D.
7.已知 的值如下表所示:如果 与 呈线性相关且回归直线方程为 ,
则 ( )
2 3 4 5
5 4 7
A. B. C. D.
iz 21−=
i2 i2−
}{ na 11 =a
+=
−
−
1
1
1
2
1
n
nn aaa }{ na
P ( )3,3−
3
2,32
π
6
5,32
π
−
6
5,32
π
−
3
2,32
π
( ) 136 23 +−+= xxaxxf ( )2,1 a
( )3,−∞− ( ]3,−∞−
−∞−
4
7,
−−
4
7,3
6,2
π
16sin =
− πθρ
5 3 1 2
yx, y x 2
7
7
4 += xy
=m
x
y m
14
81 6 7 5
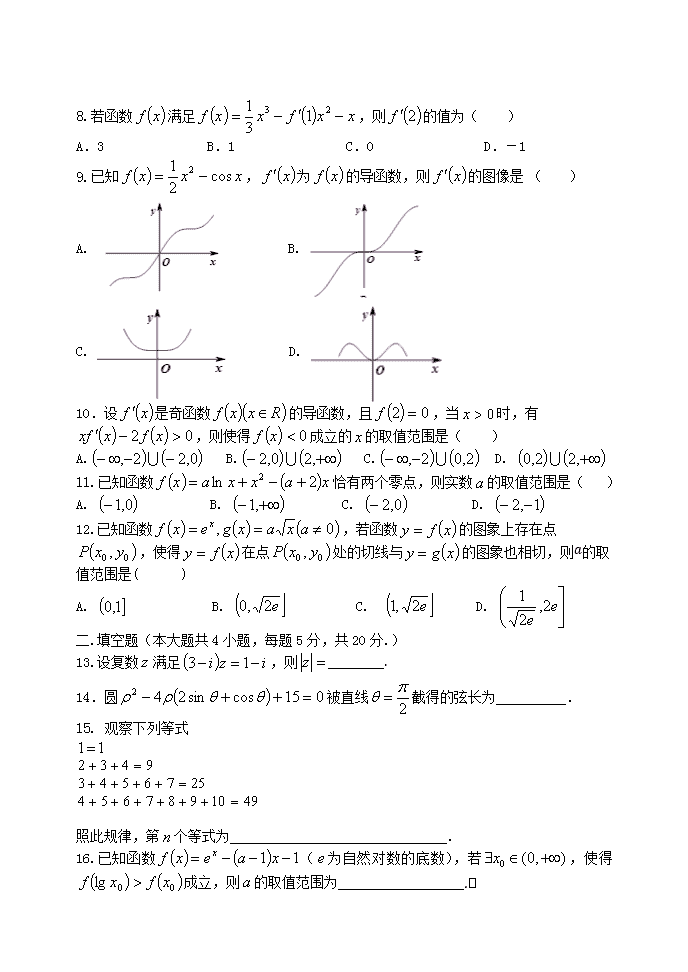
8.若函数 满足 ,则 的值为( )
A.3 B.1 C.0 D.-1
9.已知 , 为 的导函数,则 的图像是 ( )
A. B.
C. D.
10.设 是奇函数 的导函数,且 ,当 时,有
,则使得 成立的 的取值范围是( )
A. B. C. D.
11.已知函数 恰有两个零点,则实数 的取值范围是( )
A. B. C. D.
12.已知函数 ,若函数 的图象上存在点
,使得 在点 处的切线与 的图象也相切,则푎的取
值范围是( )
A. B. C. D.
二.填空题(本大题共 4 小题,每题 5 分,共 20 分.)
13.设复数 满足 ,则 ________.
14.圆 被直线 截得的弦长为__________.
15. 观察下列等式
照此规律,第 个等式为_______________________________.
16.已知函数 ( 为自然对数的底数),若 ,使得
成立,则 的取值范围为__________________.
( )xf ( ) ( ) xxfxxf −′−= 23 13
1 ( )2f ′
( ) xxxf cos2
1 2 −= ( )xf ′ ( )xf ( )xf ′
( )xf ′ ( )( )Rxxf ∈ ( ) 02 =f 0>x
( ) ( ) 02 >−′ xfxfx ( ) 0
a
三.解答题(本大题共 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤.)
17.(本小题 10 分)已知 为实数,设复数 .
(1)当复数 为纯虚数时,求 的值;
(2)当复数 对应的点在直线 的下方,求 的取值范围。
18. (本小题 12 分) 为了解人们对“延迟退休年
龄政策”的态度,某部门从年龄在 15 岁到 65 岁的
人群中随机调查了 100 人,并得到如图所示的频率
分布直方图,在这 100 人中不支持“延迟退休年龄
政策”的人数与年龄的统计结果如表所示:
年龄 不支持“延迟退休年龄政策”的人数
15
5
15
23
17
(1)由频率分布直方图,估计这 100 人年龄的平均数;(写出必要的表达式)
(2)根据以上统计数据补全下面的 列联表,据此表,能否在犯错误的概率不超过
的前提下,认为以 45 岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差
异?
45 岁以下 45 岁以上 总计
不支持
支持
总计
附:临界值表、公式:
0.15 0.10 0.050 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
,其中
m ( ) ( )immmmz 15265 22 −−+++=
z m
z 07 =+− yx m
[ )25,15
[ )35,25
[ )45,35
[ )55,45
[ )65,55
22×
05.0
( )kKP ≥2
k
( )
( )( )( )( )dbcadcba
bcadnK ++++
−=
2
2 dcban +++=
19 .( 本 小 题 12 分 ) 在 直 角 坐 标 系 中 , 直 线 的 参 数 方 程 为
.以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,已
知曲线 的极坐标方程为 .
(1)求直线 的普通方程及曲线 的直角坐标方程;
(2)若直线 与曲线 交于 两点, ,求 .
20.(本题满分 12 分)已知在平面直角坐标系 中,直线푙的参数方程为
,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为 ,点 的极坐标是 .
(1)求直线 的极坐标方程及点 到直线푙的距离;
(2)若直线 与曲线 交于 两点,求 的面积.
21.(本小题 12 分)
已知函数 ,其中 .
(1)当 时,求曲线 在点 处的切线方程;
(2)若不等式 在定义域内恒成立,求实数 的取值范围.
22.(本小题 12 分)
已知函数 ,
(1)讨论 的单调性;
(2)若 ,证明:对任意的 , .
山西大学附中
xoy l
( )为参数t
ty
tx
+=
−−=
2
22
2
21
x
C θθρ sincos2 =
l C
l C BA, ( )2,1−P PBPA ⋅
xoy
( )为参数t
ty
tx
=
=
2
3
2
1
x C
02cos22 =−− θρρ P
3
2,3
152 π
l P
l C NM , PMN∆
( ) 2xf x e mx= + 0m ≤
1m = − ( )y f x= ( )( )0, 0f
( ) 0f x > m
( )
xe
mxxxf 12 ++= Rm∈
( )xf
( )0,1−∈m [ ]mxx −∈ 1,1, 21
( ) 54 21 <+ xxf
2018~2019 学年高二第二学期 5 月(总第四次)模块诊断
数学试题(文科)
考试时间:110 分钟 满分:150 分
二. 选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,
只有一个是符合题目要求的.)
DCBAB CBAAC AB
二.填空题(本大题共 4 小题,每题 5 分,共 20 分.)
2
三.解答题(本大题共 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤.)
17.解:(1)由题意得:{█(푚^2 + 5푚 + 6 = 0@푚^2 ― 2푚 ― 15 ≠ 0) ,解之得{█(
푥 = ―2" " 或" " 푥 = ―3@푥 ≠ ―5" " 且" " 푥 ≠ ―3) ,所以푚 = ―2。
(2)复数푧对应的点的坐标为(푚2 + 5푚 + 6, 푚2 ― 2푚 ― 15),
直线푥 ― 푦 + 7 = 0的下方的点的坐标(푥,푦)应满足푥 ― 푦 + 7 > 0,
即:(푚2 + 5푚 + 6) ― (푚2 ― 2푚 ― 15) +7 > 0,
解之得푚 > ―4,所以푚的取值范围为( ―4, + ∞)。
18.解:(1)估计这 100 人年龄的平均数为
푥 = 20 × 0.2 + 30 × 0.1 + 40 × 0.2 + 50 × 0.3 + 60 × 0.3 = 42.
(2)由频率分布直方图可知,得年龄在[25,35),[35,45),[45,55)这三组内的频率和为0.5,
所以 45 岁以下共有 50 人,45 岁以上共有 50 人.
列联表如下:
45 岁以下 45 岁以上 总计
不支持 35 45 80
支持 15 5 20
总计 50 50 100
所以푘 = 100(35 × 5 ― 45 × 15)2
50 × 50 × 80 × 20 = 25
4 = 6.25 > 3.841,
所以能在犯错误的概率不超过 5%的前提下,认为以 45 岁为分界点的不同人群对“延迟退
休年龄政策”的不支持态度存在差异.
19.(1)直线的普通方程为 .
由 ,得 ,
则 ,故曲线 的直角坐标方程为 .
(2)将 ,代人 ,得 ,
则 ,
故 .
20.解:(1)由{ 푥 = 1
2푡
푦 = 3
2 푡 消去푡,
(1, )+∞
得到푦 = 3푥,
则휌sin휃 = 3휌cos휃,
∴휃 = 휋
3,
所以直线푙的极坐标方程为휃 = 휋
3(휌 ∈ 푅).
点푃(2 15
3 ,2휋
3 )到直线푙的距离为푑 = 2 15
3 × sin(2휋
3 ― 휋
3) = 2 15
3 × 3
2 = 5.
(2)由{휌2 ― 2휌푐표푠휃 ― 2 = 0
휃 = 휋
3 ,
得휌2 ―휌 ― 2 = 0,
所以휌1 + 휌2 = 1,휌1휌2 = ―2,
所以|푀푁| = |휌1 ― 휌2| = (휌1 + 휌2)2 ― 4휌1휌2 = 3,
则훥푃푀푁的面积为푆훥푃푀푁 = 1
2|푀푁| × 푑 = 1
2 × 3 × 5 = 3 5
2 .
21.解:(1)当 时, ,
∴ ,则 .
又 ,∴曲线 在点 处的切线方程为 .
(2)函数 的定义域为 ,且 .
①当 时, 恒成立,满足条件;
②当 时,由 ,得 ,所以函数 在
上单调递增;
同理函数 在 上单调递减.
因此 在 处取得最小值 .
∴ ,解得 .
综上所述,当 时,不等式 在定义域 内恒成立.
22.解:(1)푓/(푥) = ― 푥2 + (2 ― 푚)푥 + 푚 ― 1
푒푥 = ― (푥 ― 1)[푥 ― (1 ― 푚)]
푒푥
①当 1>1-m,即 m>0 时,(-∞,1-m)和(1,+∞)上 f′(x)<0,f(x)单调减;
(1-m,1)上 f′(x)>0,f(x)单调增
②当 1=1-m,即 m=0 时,(-∞,+∞)上 f′(x)<0,f(x)单调减
③当 1<1-m,即 m<0 时,(-∞,1)和(1-m,+∞)上 f′(x)<0,f(x)单调减;
(1,1-m)上 f′(x)>0,f(x)单调增
(2)对任意的 x1,x2∈[1,1-m],4f(x1)+x2<5 可转化为푓(푥1)< ― 1
4푥2 + 5
4,
设 g(x)=-1
4x+5
4,则问题等价于 x1,x2∈[1,1-m],f(x)max<g(x)min
由(1)知,当 m∈(-1,0)时,f(x)在[1,1-m]上单调递增,푓(푥)푚푎푥 = 푓(1 ― 푚) =
1m = − ( ) 2xf x e x= −
( ) 22 1xf x e′ = − ( )0 1f ′ =
( )0 1f = ( )y f x= ( )( )0, 0f 1y x= +
( )f x ( , )−∞ +∞ ( ) 2 )0(2 xf x e m m′ = + ≤
0m = ( ) 2 0xf x e= >
0m < ( ) 0f x′ > 1 ln2 2
mx > −
( )f x 1 ln ,2 2
m − +∞
( )f x 1, ln2 2
m −∞ −
( )f x 1 ln2 2
mx = − ln 12 2
m m − −
ln 1 02 2
m m − − > 2 0e m− < <
( ]2 ,0m e∈ − ( ) 0f x > ( , )−∞ +∞
2 ― 푚
푒1―푚 ,
g(x)在[1,1-m]上单调递减,푔(푥)푚푖푛 = 푔(1 ― 푚) = 1
4푚 + 1,
即证2 ― 푚
푒1―푚 <1
4푚 + 1,化简得 4(2-m)<e1-m[5-(1-m)]
令 1-m=t,t∈(1,2)
设 h(t)=et(5-t)-4(t+1),t∈(1,2),
h′(t)=et(4-t)-4>2et-4>0,故 h(t)在(1,2)上单调递增.
∴h(t)>h(1)=4e-8>0,即 4(2-m)<e1-m[5-(1-m)]
故2 ― 푚
푒1―푚 <1
4푚 + 1,得证.