高考数学【理科】真题分类详细解析版专题9 立体几何（三视图和线面关系）（解析版）

高考数学【理科】真题分类详细解析版专题9 立体几何（三视图和线面关系）（解析版）

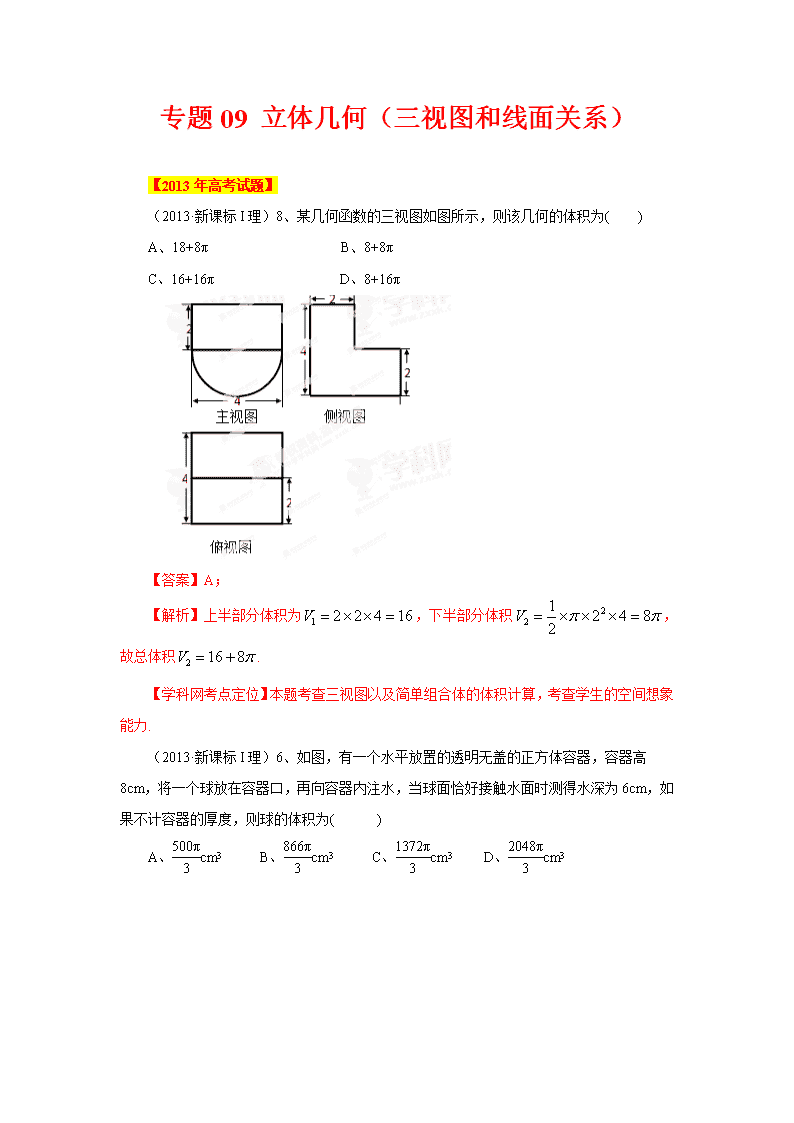
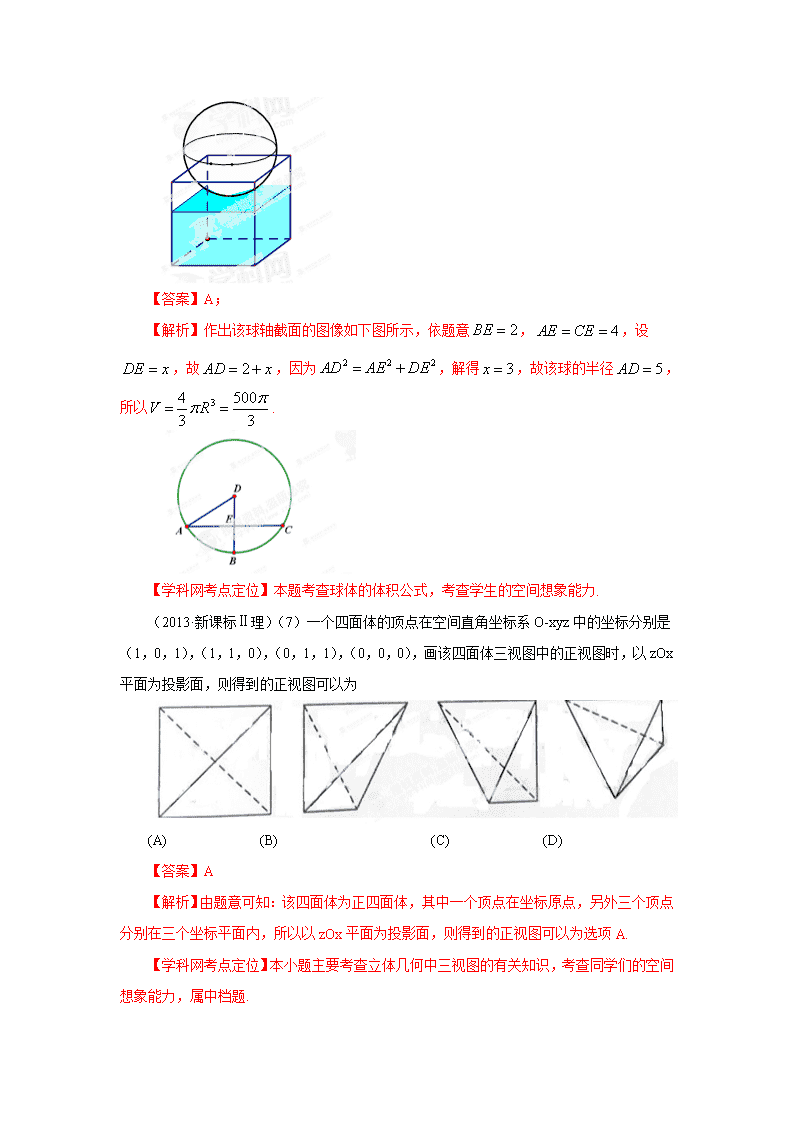
专题09 立体几何（三视图和线面关系）‎ ‎【2013年高考试题】‎ ‎（2013·新课标I理）8、某几何函数的三视图如图所示，则该几何的体积为( )‎ A、18+8π B、8+8π C、16+16π D、8+16π ‎ ‎ ‎【答案】A；‎ ‎【解析】上半部分体积为，下半部分体积，故总体积.‎ ‎【学科网考点定位】本题考查三视图以及简单组合体的体积计算，考查学生的空间想象能力.‎ ‎（2013·新课标I理）6、如图，有一个水平放置的透明无盖的正方体容器，容器高‎8cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为‎6cm，如果不计容器的厚度，则球的体积为( )‎ A、cm3 B、cm‎3‎ C、cm3 D、cm3‎ ‎【答案】A；‎ ‎【解析】作出该球轴截面的图像如下图所示，依题意，，设，故，因为，解得，故该球的半径，所以.‎ ‎【学科网考点定位】本题考查球体的体积公式，考查学生的空间想象能力.‎ ‎（2013·新课标Ⅱ理）（7）一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为 ‎(A) (B) (C) (D)‎ ‎【答案】A ‎【解析】由题意可知：该四面体为正四面体，其中一个顶点在坐标原点，另外三个顶点分别在三个坐标平面内，所以以zOx平面为投影面，则得到的正视图可以为选项A.‎ ‎【学科网考点定位】本小题主要考查立体几何中三视图的有关知识，考查同学们的空间想象能力，属中档题.‎ ‎（2013·浙江理）12、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积等于________。‎ ‎【答案】24‎ ‎【解析】三视图问题关键是搞清楚几何体的直观图的构成，根据三视图的信息确定直观图中的边的长度和角的度数，然后利用体积公式求解。此题中的正视图和侧视图都是三角形，且俯视图是直角三角形，所以原图是直三棱柱被平面截后所剩余的几何体。注意长对正，宽相等，高平齐的法则。即由已知得此几何体的直观图是一个底面是直角三角形且两直角边分别是3,4高是5的直三棱柱在上面截去一个三棱锥，三棱锥从一个顶点出发的三条棱两两垂直，底面边长分别是3,4高是3，如图3所示，红色为截去的三棱锥，所以体积为；‎ ‎【学科网考点定位】此题考查三视图知识、多面体的体积计算公式，考查学生的空间想象能力；‎ ‎（2013·浙江理）10.在空间中，过点作平面的垂线，垂足为，记。设是两个不同的平面，对空间任意一点，,恒有 ‎，则（ ）‎ 平面与平面垂直 B. 平面与平面所成的（锐）二面角为 ‎ C. 平面与平面平行 D.平面与平面所成的（锐）二面角为 ‎ ‎【答案】A ‎【解析】此题关键是搞清楚“在空间中，过点作平面的垂线，垂足为，记。”这句话的意思，即，其中垂直，此题的关键和注意的地方是要对题目所描述的内容正确理解；设所以，由已知得到：于，于，于，于，且恒成立，即与重合，即当时满足；如图2所示：‎ ‎【学科网考点定位】此题是信息类题目，考查线面垂直和面面垂直的知识点，考查学生的自学能力和运用所学知识解决问题的能力；‎ 本解析为学科网名师解析团队原创，授权学科网独家使用，如有盗用，依法追责！‎ ‎（2013·陕西理）12. 某几何体的三视图如图所示, 则其体积为 .‎ ‎【答案】‎ ‎【解析】由三视图还原为实物图得半个圆锥，其体积．‎ ‎【学科网考点定位】本题主要考查了三视图还原为实物图的能力和圆锥的体积公式，属于容易题，‎ ‎（2013·辽宁理）（13）某几何体的三视图如图所示，则该几何体的体积是 .‎ ‎【答案】‎ ‎【解析】由三视图可知，直观图为一个圆柱体中间挖去一个 ‎ 正四棱柱。‎ ‎【学科网考点定位】本题考查三视图及空间几何体的体积计算。‎ ‎（2013·江西理）8.如果，正方体的底面与正四面体的底面在同一平面α上，且AB//CD，正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m，n，那么m+n=（ ）‎ A.8 B.9 C.10 D.11‎ ‎【答案】A ‎【解析】因为过EF做垂直于CD（AB）的平面垂直平分CD，所以该平面与过AB中点并与AB垂直的平面平行，平面和正方体的4个侧面相交，由于EF和正方体的侧棱不平行，所以它与正方体的六个面所在的平面相交的平面个数为4.同理与CE相交的平面有4个，共8个，选A.‎ ‎【学科网考点定位】该题主要考查空间点、线、面的位置关系，考查空间直线与平面的平行与相交，考查空间想象能力和逻辑思维能力.‎ ‎（2013·湖南理）7．已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能等于（ ）‎ A． B． C． D． ‎ ‎【答案】C；‎ ‎【解析】正方体的正视图面积应当介意1与之间，故C不正确.‎ ‎【学科网考点定位】本题考查三视图，考查学生的空间想象能力.‎ ‎（2013·广东理）5．某四棱台的三视图如图所示,则该四棱台的体积是 ( )‎ A . B． ‎ C． D．‎ ‎【答案】B ‎【解析】由三视图可知,该四棱台的上下底面边长分别为和的正方形,高为,故 ‎,故选B．‎ ‎【学科网考点定位】三视图与四棱台的体积 ‎（2013·福建理）12. 已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、‎ 俯视图、均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是_____ ‎ ‎ 【答案】 ‎ ‎【解析】由三视图可知几何体为球内接一个正方体，所以正方体的体对角线为球的直径，。‎ ‎【学科网考点定位】对于三视图的考查主要考查学生的空间思维能力，要有较好的空间感。属于中等难度。‎ ‎（2013·广东理）6．设是两条不同的直线,是两个不同的平面,下列命题中正确的是( )‎ A . 若,,,则 B．若,,,则 C．若,,,则 D．若,,,则 ‎【答案】D ‎【解析】选项A中，m与n还可能平行或者异面，故错；B中，m与n还可能异面，故错；C中，还有可能平行或者相交，故错； D中，故D正确.‎ ‎【学科网考点定位】考查线面的位置关系 ‎【2012年高考试题】‎ ‎1.【2012高考真题新课标理7】如图，网格纸上小正方形的边长为，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）‎ ‎ ‎ ‎【答案】B ‎【解析】由三视图可知，该几何体是三棱锥，底面是俯视图，高为，所以几何体的体积为,选B.‎ ‎2.【2012高考真题浙江理10】已知矩形ABCD，AB=1，BC=。将△沿矩形的对角线BD所在的直线进行翻折，在翻折过程中。‎ A.存在某个位置，使得直线AC与直线BD垂直.‎ B.存在某个位置，使得直线AB与直线CD垂直.‎ C.存在某个位置，使得直线AD与直线BC垂直.‎ D.对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直 ‎ 【答案】C ‎【解析】最简单的方法是取一长方形动手按照其要求进行翻着，观察在翻着过程，即可知选项C是正确的．‎ ‎3.【2012高考真题新课标理11】已知三棱锥的所有顶点都在球的求面上，是边长为的正三角形，为球的直径，且；则此棱锥的体积为（ ）‎ ‎ ‎ ‎【答案】A ‎【解析】的外接圆的半径，点到面的距离4.【2012高考真题四川理6】下列命题正确的是（ ）‎ A、若两条直线和同一个平面所成的角相等，则这两条直线平行 B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 D、若两个平面都垂直于第三个平面，则这两个平面平行 ‎【答案】C ‎【解析】A.两直线可能平行，相交，异面故A不正确；B.两平面平行或相交；C.正确；D.这两个平面平行或相交.‎ ‎5.【2012高考真题四川理10】如图，半径为的半球的底面圆在平面内，过点作平面的垂线交半球面于点，过圆的直径作平面成角的平面与半球面相交，所得交线上到平面的距离最大的点为，该交线上的一点满足，则、两点间的球面距离为（ ）‎ ‎ B、 C、 D、‎ ‎【答案】A ‎ ‎ ‎【解析】根据题意，易知平面AOB⊥平面CBD,‎ ‎,，由弧长公式易得，、两点间的球面距离为.‎ ‎6.【2012高考真题陕西理5】如图，在空间直角坐标系中有直三棱柱，，则直线与直线夹角的余弦值为（ ）‎ A. B. C. D. ‎ ‎【答案】A.‎ ‎【解析】设，则，，‎ ‎，，故选A.‎ ‎7.【2012高考真题湖南理3】某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是 ‎【答案】D ‎【解析】本题是组合体的三视图问题，由几何体的正视图和侧视图均如图1‎ 所示知，原图下面图为圆柱或直四棱柱，上面是圆柱或直四棱柱或下底是直角的三棱柱，Ａ，Ｂ，Ｃ都可能是该几何体的俯视图，Ｄ不可能是该几何体的俯视图，因为它的正视图上面应为如图的矩形.‎ ‎9.【2012高考真题广东理6】某几何体的三视图如图所示，它的体积为 A．12π B.45π C.57π D.81π ‎【答案】C ‎ ‎ ‎【解析】该几何体的上部是一个圆锥，下部是一个圆柱，根据三视图中的数量关系，可得．故选C．‎ ‎ ‎ ‎10.【2012高考真题福建理4】一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是 A.球 B.三棱柱 C.正方形 D.圆柱 ‎【答案】D.‎ ‎【解析】球的三视图全是圆；如图正方体截出的三棱锥三视图全是等腰直角三角形；正方体三视图都是正方形.可以排除ABC，故选Ｄ．‎ ‎11.【2012高考真题重庆理9】设四面体的六条棱的长分别为1，1，1，1，和，且长为的棱与长为的棱异面，则的取值范围是 ‎（A） （B） （C） （D）‎ ‎ 【答案】A ‎ ‎【解析】因为则，，选A，‎ ‎12.【2012高考真题北京理7】某三棱锥的三视图如图所示，该三梭锥的表面积是（ ）‎ A. 28+6 B. 30+‎6‎ C. 56+ 12 D. 60+12‎ ‎【答案】B ‎【解析】从所给的三视图可以得到该几何体为三棱锥，如图所示，图中蓝色数字所表示的为直接从题目所给三视图中读出的长度，黑色数字代表通过勾股定理的计算得到的边长。本题所求表面积应为三棱锥四个面的面积之和，利用垂直关系和三角形面积公式，可得：，，，，因此该几何体表面积，故选B。‎ ‎13.【2012高考真题全国卷理4】已知正四棱柱ABCD- A1B‎1C1D1中 ，AB=2，CC1= E为CC1的中点，则直线AC1与平面BED的距离为 A 2 B C D 1‎ ‎【答案】D ‎【解析】连结交于点，连结，因为是中点，所以,且，所以，即直线 与平面BED的距离等于点C到平面BED的距离，过C做于,则即为所求距离.因为底面边长为2，高为，所以,,,所以利用等积法得，选D. ‎ ‎14.【2012高考真题浙江理11】已知某三棱锥的三视图（单位：cm）如图所示，则该三棱锥的体积等于________cm3.‎ ‎【答案】1‎ ‎【解析】观察三视图知该三棱锥的底面为一直角三角形，右侧面也是一直角三角形．故体积等于．‎ ‎15.【2012高考真题四川理14】如图，在正方体中，、分别是、的中点，则异面直线与所成角的大小是____________。‎ ‎【答案】‎ ‎【解析】本题有两种方法，一、几何法：连接，则,又，易知，所以与所成角的大小是；二、坐标法：建立空间直角坐标系，利用向量的夹角公式计算得异面直线与所成角的大小是.‎ ‎ 16.【2012高考真题辽宁理13】一个几何体的三视图如图所示，则该几何体的表面积为______________。‎ ‎【答案】38‎ ‎22.【2012高考真题安徽理12】某几何体的三视图如图所示，该几何体的表面积是．‎ ‎【答案】92‎ ‎【解析】该几何体是底面是直角梯形，高为的直四棱柱，‎ 几何体的表面积是．‎ ‎23.【2012高考真题天津理10】一个几何体的三视图如图所示（单位：m），则该几何体的体积为_________m3. ‎ ‎【答案】‎ ‎【解析】根据三视图可知，这是一个上面为长方体，下面有两个直径为3的球构成的组合体，两个球的体积为，长方体的体积为，所以该几何体的体积为。‎ ‎【2011年高考试题】‎ 一、选择题:‎ ‎1. (2011年高考山东卷理科11)下图是长和宽分别相等的两个矩形．给定下列三个命题：‎ ‎①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如 下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是 ‎(A)3 (B)2 (C)1 (D)0‎ ‎【答案】A ‎【解析】对于①,可以是放倒的三棱柱；容易判断②③可以.‎ ‎2.(2011年高考浙江卷理科3)若某几何体的三视图如图所示，则这个几何体的直观图可以是 ‎4.(2011年高考安徽卷理科6)一个空间几何体得三视图如图所示，则该几何体的表面积为 ‎ ‎ ‎ （A） 48 (B)32+8 (C) 48+8 (D) 80‎ ‎【答案】C ‎【命题意图】本题考查三视图的识别以及空间多面体表面积的求法.‎ ‎【解析】由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2，下底为4，高为4，。故 ‎【解题指导】：三视图还原很关键，每一个数据都要标注准确。‎ ‎5.(2011年高考辽宁卷理科8)如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（ ）‎ ‎(A) AC⊥SB ‎ ‎(B) AB∥平面SCD ‎ ‎(C) SA与平面SBD所成的角等于SC与平面SBD所成的角 ‎ ‎(D)AB与SC所成的角等于DC与SA所成的角 答案： D 解析：对于A:因为SD⊥平面ABCD，所以DS⊥AC.因为四边形ABCD为正方形，所以AC⊥BD，故AC⊥平面ABD,因为SB平面ABD,所以AC⊥SB，正确.对于B：因为AB//CD,所以AB//平面SCD.对于C:设.因为AC⊥平面ABD，所以SA和SC在平面SBD内的射影为SO，则∠ASO和∠CSO就是SA与平面SBD所成的角和SC 与平面SBD所成的角，二者相等，正确.故选D.‎ ‎6.(2011年高考辽宁卷理科12)已知球的直径SC=4，A,B是该球球面上的两点，AB=，，则棱锥S-ABC的体积为（ ）‎ ‎（A） （B） （C） （D）1‎ 第6题图 答案：D 解析：由主视图和府视图可知，原几何体是由后面是半个圆锥，前面是三棱锥的组合体，所以，左视图是D.‎ 点评：本题考查三视图、直观图及他们之间的互化，同时也考查空间想象能力和推理能力，要求有扎实的基础知识和基本技能。‎ ‎8．(2011年高考江西卷理科8)已知，，是三个相互平行的平面．平面，之间的距离为，平面，之间的距离为．直线与，，分别相交于，，，那么“=”是“”的 ‎ A.充分不必要条件 B.必要不充分条件 ‎ C．充分必要条件 D．既不充分也不必要条件 ‎【答案】C ‎【解析】过点作平面的垂线g,交平面，分别于点A、B两点,由两个平面平行的性质可知∥,所以,故选C.‎ ‎3‎ ‎3‎ ‎2‎ 正视图 侧视图 俯视图 图1‎ ‎9. (2011年高考湖南卷理科3)设图1是某几何体的三视图，则该几何体的体积为 ‎ A. B. C. D. ‎ 答案：B 解析：由三视图可以还原为一个底面为边长是3的正方形，‎ 高为2的长方体以及一个直径为3的球组成的简单几何体，‎ 其体积等于。故选B 评析：本小题主要考查球与长方体组成的简单几何体的三视图 以及几何体的体积计算.‎ ‎10.(2011年高考广东卷理科7)如图l—3．某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为（ ）‎ ‎ A. B. C. D.‎ ‎【解析】B.由题得三视图对应的直观图是如图所示的直四棱柱，‎ ‎。所以选B ‎11.(2011年高考陕西卷理科5)某几何体的三视图如图所示，则它的体积是 ‎ ‎ （A）（B） ‎ ‎（C）（D）‎ ‎【答案】A ‎【解析】：由三视图可知该几何体为立方体与圆锥，‎ 立方体棱长为2，圆锥底面半径为1、高为2，‎ 所以体积为故选A ‎12.(2011年高考重庆卷理科9)高为的四棱锥S-ABCD的底面是边长为1的正方形，点S、A、B、C、D均在半径为1的同一球面上，则底面ABCD的中心与顶点S之间的距离为 ‎（A） （B） ‎ ‎（C）1 （D）‎ 解析：选C. 设底面中心为G，球心为O，则易得，于是 ‎，用一个与ABCD所在平面距离等于的平面去截球，S便为其中一个交点，此平面的中心设为H，则，故，故 ‎13．(2011年高考四川卷理科3)，，是空间三条不同的直线，则下列命题正确的是( )‎ ‎ (A)， （B），‎ ‎(C) ，，共面 （D），，共点，，共面 ‎【答案】C ‎【解析】如图，作于，由为直二面角，，得平面，进而,又,,‎ 于是平面。故为到平面的距离。‎ 在中，利用等面积法得 ‎15. (2011年高考全国卷理科11)已知平面截一球面得圆M，过圆心M且与成，二面角的平面截该球面得圆N，若该球的半径为4，圆M 的面积为4，则圆N的面积为 ‎ (A) (B) (c) (D)‎ ‎【答案】D ‎【解析】：由圆的面积为得，‎ ‎，在 ‎ 故选D ‎ ‎16．(2011年高考北京卷理科7)某四面体的三视图如图所示，该四面体四个面的面积中，最大的是 ‎ A．8 B． C．10 D．‎ ‎【答案】C ‎17.(2011年高考辽宁卷理科15)一个正三棱柱的侧棱长和底面边长相等，体积为，它的三视图中的俯视图如右图所示，左视图是一个矩形，则这个矩形的面积是____________.‎ 答案： ‎ 解析：设正三棱柱的侧棱长和底面边长为a，则由，解得a=2‎ ‎，正三棱柱的左视图与底面一边垂直的截面大小相同，故该矩形的面积是.‎ ‎18．(2011年高考天津卷理科10)一个几何体的三视图如图所示（单位：），则这个几何体 的体积为__________ ‎ ‎【答案】‎ ‎【解析】由题意知,该几何体为一个组合体,其下面是一个长方体(长为3m,宽为2m,‎ 高为1m),上面有一个圆锥(底面半径为1,高为3),所以其体积为.‎ ‎19. (2011年高考四川卷理科15)如图，半径为R的球O中有一内接圆柱.当圆柱的侧面积最大时，求球的表面积与该圆柱的侧面积之差是 . ‎ 答案：‎ 解析：时，，则 ‎【2010高考试题】‎ ‎（2010浙江理数）（6）设，是两条不同的直线，是一个平面，则下列命题正确的是 ‎（A）若，，则 （B）若，，则 ‎（C）若，，则 （D）若，，则 解析：选B，可对选项进行逐个检查。本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理，也蕴含了对定理公理综合运用能力的考察，属中档题。‎ ‎（2010全国卷2理数）（11）与正方体的三条棱、、所在直线的距离相等的点 ‎（A）有且只有1个 （B）有且只有2个 ‎（C）有且只有3个 （D）有无数个 ‎【答案】D ‎【解析】直线上取一点，分别作垂直于于则 ‎（2010全国卷2理数）（9）已知正四棱锥中，，那么当该棱锥的体积最大时，它的高为 ‎（A）1 （B） （C）2 （D）3‎ ‎【答案】C ‎【命题意图】本试题主要考察椎体的体积，考察告辞函数的最值问题.‎ ‎【解析】设底面边长为a，则高所以体积，‎ 设，则，当y取最值时，，解得a=0或a=4时，体积最大，此时，故选C.‎ ‎（2010辽宁理数）(12) (12)有四根长都为2的直铁条，若再选两根长都为a的直铁条，使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架，则a的取值范围是 ‎ (A)（0,） (B)（1,）‎ ‎ (C) (,） (D) （0,）‎ ‎【答案】A ‎【解析】根据条件，四根长为2的直铁条与两根长为a的直铁条要组成三棱镜形的铁架，有以下两种情况：（1）地面是边长为2的正三角形，三条侧棱长为2，a，a，如图，此时a可以取最大值，可知AD=，SD=，则有<2+，即，即有a<‎ ‎(2)构成三棱锥的两条对角线长为a，其他各边长为2，如图所示，此时a>0;‎ 综上分析可知a∈（0,）‎ ‎（2010江西理数）10.过正方体的顶点A作直线L，使L与棱,,所成的角都相等，这样的直线L可以作 A.1条 B.2条 C.3条 D.4条 ‎【答案】D ‎【解析】考查空间感和线线夹角的计算和判断，重点考查学生分类、划归转化的能力。第一类：通过点A位于三条棱之间的直线有一条体对角线AC1，第二类：在图形外部和每条棱的外角和另2条棱夹角相等，有3条，合计4条。 ‎ ‎（2010四川理数）（11）半径为的球的直径垂直于平面，垂足为，是平面内边长为的正三角形，线段、分别与球面交于点M，N，那么M、N两点间的球面距离是 ‎（A） （B） w_w_w.k*s 5*u.c o*m ‎（C） （D）‎ 解析：由已知，AB＝2R,BC＝R,故tan∠BAC＝ w_w_w.k*s 5*u.c o*m cos∠BAC＝‎ 连结OM，则△OAM为等腰三角形 AM＝2AOcos∠BAC＝，同理AN＝，且MN∥CD w_w_w.k*s 5*u.c o*m 而AC＝R,CD＝R 故MN：CD＝AN:AC w_w_w.k*s 5*u.c o*m Þ MN＝，‎ 连结OM、ON，有OM＝ON＝R 于是cos∠MON＝‎ 所以M、N两点间的球面距离是 w_w_w.k*s 5*u.c o*m 答案：A ‎（2010山东理数）(3)在空间，下列命题正确的是 ‎（A）平行直线的平行投影重合 ‎（B）平行于同一直线的两个平面平行 ‎（C）垂直于同一平面的两个平面平行 ‎（D）垂直于同一平面的两条直线平行 ‎【答案】D ‎【解析】由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以得出答案。‎ ‎1.（2010安徽理数）8、一个几何体的三视图如图，该几何体的表面积为 A、280 B、‎292 ‎C、360 D、372‎ ‎【答案】C ‎【解析】该几何体由两个长方体组合而成，其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和。.‎ ‎【方法技巧】把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体，画出直观图，得出各个棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。‎ ‎（2010浙江理数）（12）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是___________ .‎ 解析：图为一四棱台和长方体的组合体的三视图，由卷中所给公式计算得体积为144，本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算，属容易题 ‎（2010辽宁理数）（15）如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.‎ ‎【答案】‎ ‎【解析】由三视图可知，此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥，所以最长棱长为 ‎（2010江西理数）16.如图，在三棱锥中，三条棱，，两两垂直，且>>,分别经过三条棱，，作一个截面平分三棱锥的体积，截面面积依次为，，，则，，的大小关系为 。‎ ‎【答案】 ‎ ‎【解析】考查立体图形的空间感和数学知识的运用能力，通过补形，借助长方体验证结论，特殊化，令边长为1，2，3得。‎ ‎（2010四川理数）（15）如图，二面角的大小是60°，线段.，与所成的角为30°.则与平面所成的角的正弦值是 .‎ 解析：过点A作平面β的垂线，垂足为C，在β内过C作l的垂线.垂足为D 连结AD，有三垂线定理可知AD⊥l，‎ C D 故∠ADC为二面角的平面角，为60°‎ 又由已知，∠ABD＝30°‎ 连结CB，则∠ABC为与平面所成的角w_w_w.k*s 5*u.c o*m 设AD＝2，则AC＝，CD＝1‎ AB＝＝4‎ ‎∴sin∠ABC＝‎ 答案：‎ ‎（2010天津理数）（12）一个几何体的三视图如图所示，则这个几何体的体积为 ‎ ‎【答案】‎ ‎【解析】本题主要考查三视图的概念与柱体、椎体体积的计算，属于容易题。‎ 由三视图可知，该几何体为一个底面边长为1，高为2的正四棱柱与一个底面边长为2，高为1的正四棱锥组成的组合体，因为正巳灵珠的体积为2，正四棱锥的体积为，所以该几何体的体积V=2+ = ‎ ‎（2010湖北理数）13.圆柱形容器内部盛有高度为‎8cm的水，若放入三个相同的球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是 cm。‎ ‎【答案】4‎ ‎【解析】设球半径为r，则由可得,解得r=4.‎ ‎（2010福建理数）‎ ‎12．若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于 ．‎ ‎【答案】‎ ‎【解析】由正视图知：三棱柱是以底面边长为2，高为1的正三棱柱，所以底面积为 ‎，侧面积为，所以其表面积为。K^S*5U.C#O%‎ ‎（2010浙江理数）（20）（本题满分15分）如图， 在矩形中，点分别在线段上，.沿直线将 翻折成，使平面.‎ ‎（Ⅰ）求二面角的余弦值；‎ ‎（Ⅱ）点分别在线段上，若沿直线将四边形向上翻折，使与重合，求线段的长。‎ 解析：本题主要考察空间点、线、面位置关系，二面角等基础知识，空间向量的应用，同事考查空间想象能力和运算求解能力。‎ ‎（Ⅰ）解：取线段EF的中点H，连结，因为=及H是EF的中点，所以,‎ 又因为平面平面.‎ 如图建立空间直角坐标系A-xyz 则（2，2，），C（10，8，0），‎ F（4，0，0），D（10，0，0）. ‎ 故=（-2，2，2），=（6，0，0）.‎ 设=（x,y,z）为平面的一个法向量，‎ ‎-2x+2y+2z=0‎ 所以 6x=0.‎ 取，则。‎ 所以。‎ 方法二：‎ ‎（Ⅰ）解：取线段的中点,的中点,连结。‎ ‎ 因为=及是的中点，‎ 所以 故二面角的余弦值为。‎ ‎（Ⅱ）解：设,‎ ‎ 因为翻折后，与重合，‎ 所以，‎ ‎ 而，‎ ‎ ‎ 得，‎ 经检验，此时点在线段上，‎ 所以。‎ ‎【2009高考试题】‎ ‎1. (广东文6理5)给定下列四个命题：‎ ‎①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；‎ ‎②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；‎ ‎③垂直于同一直线的两条直线相互平行；‎ ‎④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是 Ａ．①和② Ｂ．②和③ Ｃ．.③和④ Ｄ．②和④‎ 答案：D 解析：①错, ②正确, ③错, ④正确.故选D ‎2. (宁夏海南文9理8) 如图，正方体的棱线长为1，线段上有两个动点E，F，且，则下列结论中错误的是 ‎ ‎ （A）‎ ‎ （B）‎ ‎ （C）三棱锥的体积为定值 ‎ （D）异面直线所成的角为定值 解析：A正确，易证B显然正确，‎ ‎；C正确，可用等积法求得；D错误。选D.‎ ‎12.(山东文理4) 一空间几何体的三视图如图所示,则该几何体的体积为( ).‎ A. B. C. D. ‎ ‎2 ‎ ‎2 ‎ 侧(左)视图 ‎ ‎2 ‎ ‎2 ‎ ‎2 ‎ 正(主)视图 ‎ 解析：该空间几何体为一圆柱和一四棱锥组成的,‎ 圆柱的底面半径为1,高为2,体积为,四棱锥的底面 边长为，高为，所以体积为 所以该几何体的体积为.‎ 答案:C ‎3. (天津文理12) 如图是一个几何体的三视图，若它的体积是，则 ‎_______‎ ‎【考点定位】本小题考查三视图、三棱柱的体积，基础题。‎ 解析：知此几何体是三棱柱，其高为3，底面是底边长为2，底边上的高为的等腰三角形，所以有 ‎6.(浙江理17)如图，在长方形中，，，为的中点，为线段（端点除 外）上一动点．现将沿折起，使平面平面．在平面内过点 作，为垂足．设，则的取值范围是 ．‎ 答案： 解析：此题的破解可采用二个极端位置法，即对于F位于DC的中点时，，随着F点到C点时，因平面，即有，对于，又，因此有，则有，因此的取值范围是 ‎【2008高考试题】‎ ‎1.（2008·山东卷）右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是 ‎(A)9π　　　　　　　（B）10π ‎(C)11π (D)12π 解析：考查三视图与几何体的表面积。从三视图可以看出该几何体是由一个球和一个圆