浙江省2014届理科数学专题复习试题选编17：三角函数的图象与性质（学生版）

浙江省2014届理科数学专题复习试题选编17：三角函数的图象与性质（学生版）

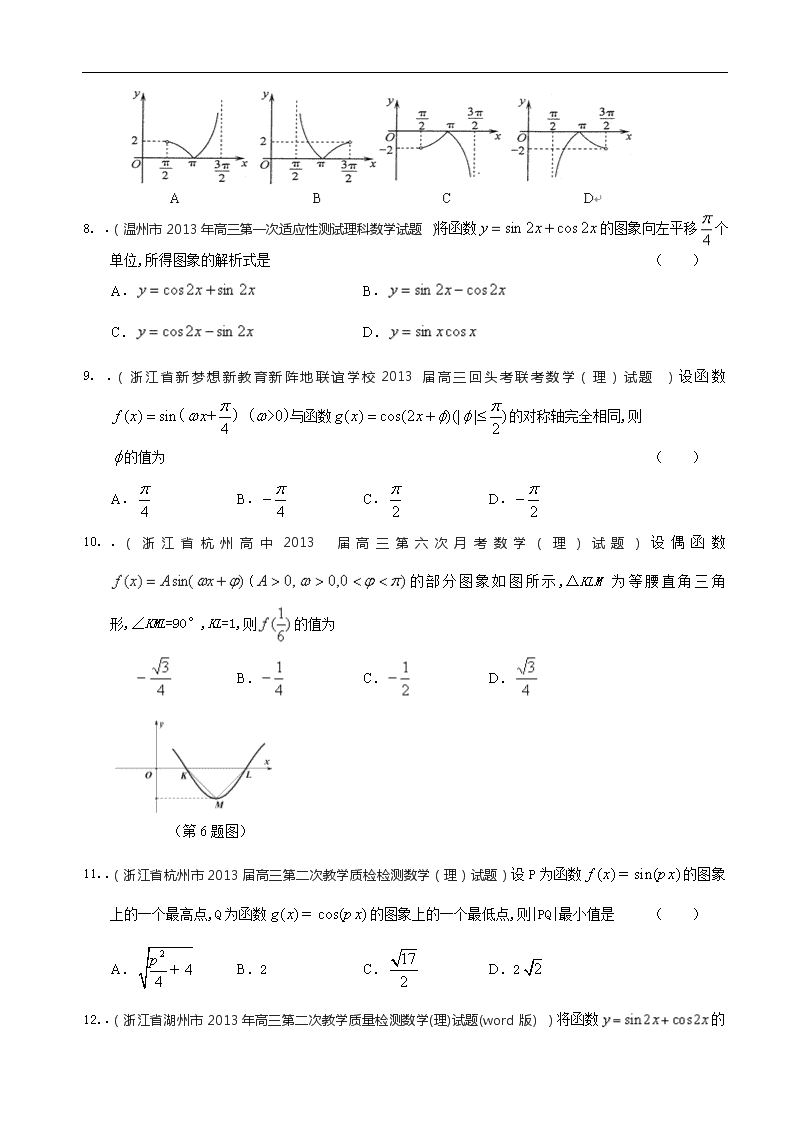
浙江省2014届理科数学专题复习试题选编17：三角函数的图象与性质 ‎、‎ 一、选择题 ．（浙江省2013年高考模拟冲刺（提优）测试二数学（理）试题）已知且有,则 （　　）‎ A． B．‎1 ‎C． D．0‎ ．（浙江省宁波市十校2013届高三下学期能力测试联考数学（理）试题）函数的图像与函数的图像所有交点的横坐标之和等于 （　　）‎ A．2 B．‎3 ‎C．4 D．6‎ ．（浙江省温岭中学2013届高三冲刺模拟考试数学（理）试题）函数的最小正周期为 （　　）‎ A． B． C． D．‎ ．（浙江省杭州市2013届高三上学期期中七校联考数学（理）试题）对于函数 (其中,),选取的一组值计算和,所得出的正确结果一定不可能是 （　　）‎ A．1和2 B．1和‎3 ‎C．2和4 D．4和6‎ ．（浙江省海宁市2013届高三2月期初测试数学（理）试题）已知函数,,则下列结论中正确的是 （　　）‎ A．函数的最小正周期为 ‎ B．函数的最大值为1 ‎ C．将函数的图象向右平移单位后得的图象 ‎ D．将函数的图象向左平移单位后得的图象 ．（【解析】浙江省镇海中学2013届高三5月模拟数学（理）试题）设函数,对任意都有,若函数,则的值为 （　　）‎ A．1 B．或‎3 ‎C． D．‎ ．（浙江省诸暨中学2013届高三上学期期中考试数学（理）试题）函数在区间(,)内的图象大致是 ．（温州市2013年高三第一次适应性测试理科数学试题）将函数的图象向左平移个单位,所得图象的解析式是 （　　）‎ A． B． ‎ C． D．‎ ．（浙江省新梦想新教育新阵地联谊学校2013届高三回头考联考数学（理）试题 ）设函数与函数的对称轴完全相同,则 的值为 （　　）‎ A． B． C． D．‎ ．（浙江省杭州高中2013届高三第六次月考数学（理）试题）设偶函数(的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则的值为 （　　）‎ A． B． C． D．‎ ‎（第6题图）‎ ．（浙江省杭州市2013届高三第二次教学质检检测数学（理）试题）设P为函数的图象上的一个最高点,Q为函数的图象上的一个最低点,则|PQ|最小值是 （　　）‎ A． B．‎2 ‎C． D．2‎ ．（浙江省湖州市2013年高三第二次教学质量检测数学(理)试题(word版) ）将函数 的图象向左平移个单位长度,所得图象对应的函数解析式可以是 （　　）‎ A． B． C． D．‎ ．（浙江省稽阳联谊学校2013届高三4月联考数学(理)试题（word版） ）已知函数的图象的两相邻对称轴间的距离为,则 （　　）‎ A． B． C． D．‎ ．（浙江省宁波市2013届高三第二次模拟考试数学（理）试题）函数是[来源:学*科*网Z*X*X*K] （　　）‎ A．周期为π的偶函数 B．周期为2π的偶函数 ‎ C．周期为π的奇函数 D．周期为2π的奇函数 ‎ ．（浙江省绍兴市2013届高三教学质量调测数学（理）试题（word版） ）函数在下列哪个区间上单调递增 （　　）‎ A． B． C． D． ‎ ．（浙江省温岭中学2013届高三高考提优冲刺考试（三）数学（理）试题 ）如图,已知四边形中,,,,,则经过某种翻折后以下线段可能会相互重合的是: ‎ ‎ （　　）‎ A． B． C． D．‎ ．（浙江省一级重点中学（六校）2013届高三第一次联考数学（理）试题）函数的部分图象如上图所示,则将 的图象向右平移个单位后,得到的图象解析式为 ‎ ‎ （　　）‎ A． B． C． D．‎ ．（浙江省2013年高考模拟冲刺（提优）测试一数学（理）试题）函数=R)的图像如图所示,如果,且 ,则 ‎ ‎（第5题）‎ ‎ （　　）‎ A．1 B． C． D．‎ ．（浙江省杭州二中2013届高三年级第五次月考理科数学试卷）已知函数,若存在,使得恒成立,则的值是 （　　）‎ A． B． C． D．‎ ．（浙江省六校联盟2013届高三回头联考理科数学试题）设函数的对称轴完全相同,则的值为 （　　）‎ A． B．- C． D．- ‎ ．（浙江省宁波市2013届高三第一学期期末考试理科数学试卷）已知函数上有两个零点,则m的取值范围是 （　　）‎ A．(1,2) B．[1,2) C．(1,2] D．[l,2]‎ ．（浙江省五校联盟2013届高三下学期第一次联考数学（理）试题）若函数对任意实数都有,则的值等于 （　　）‎ A． B．‎1 ‎C． D．‎ ．（浙江省重点中学2013届高三上学期期中联谊数学（理）试题）为得到函数的图像,只需将函数的图像 （　　）‎ A．向右平移个长度单位 B．向左平移个长度单位 ‎ C．向右平移个长度单位 D．向左平移个长度单位 ‎ ．（浙江省五校2013届高三上学期第一次联考数学（理）试题）已知函数的图象与轴的两个相邻交点的距离等于,若将函数 的图象向左平移个单位得到函数的图象,则是减函数的区间为 （　　）‎ A． B． C． D．‎ ．（浙江省温州市2013届高三第三次适应性测试数学(理)试题（word版） ）已知函数,其中,则下列结论中正确的是 （　　）‎ A．的最大值是2 B．将函数的图象左移得到函数的图象 C．是最小正周期为的偶函数 D．的一条对称轴是 ．（浙江省温岭中学2013届高三冲刺模拟考试数学（理）试题）已知函数,.已知当时,函数 ‎ 所有零点和为9.则当时,函数所有零点和为 （　　）‎ A．15 B．‎12 ‎C．9 D．与k的取值有关 ．（浙江省十校联合体2013届高三上学期期初联考数学（理）试题）已知k<-4 ,则函数y=cos2x+k(sinx-1)的最大值是 （　　）‎ A． B．-2k+1 ‎ C．-1 D．-2k-1‎ ．（浙江省名校新高考研究联盟2013届高三第一次联考数学（理）试题）当时,函数取得最小值,则函数是 （　　）‎ A．奇函数且图像关于点对称 B．偶函数且图像关于点对称 ‎ C．奇函数且图像关于直线对称 D．偶函数且图像关于点对称 ．（浙江省嘉兴市第一中学2013届高三一模数学（理）试题）函数的最小正周期是 （　　）‎ A． B．π C．2π D．4π ．（浙江省黄岩中学2013年高三5月适应性考试数学(理)试卷 ）已知函数的图象点对称,则实数的值为 （　　）‎ A． B． C． D．‎ 二、填空题 ．（温州市2013年高三第一次适应性测试理科数学试题）已知,则的最小值为____;‎ ．（浙江省“六市六校”联盟2013届高三下学期第一次联考数学（理）试题）若实数满足方程组,则=________.‎ ．（浙江省宁波市鄞州中学2012学年高三第六次月考数学（理）试卷 ）已知,,则__________;‎ ．（浙江省绍兴一中2013届高三下学期回头考理科数学试卷）已知定义在R上的函数f(x)既是奇函数,又是周期为3的周期函数,当时,,则函数f(x)在区间[0,6]上的零点个数为____________个. ‎ ．（浙江省温州中学2013届高三第三次模拟考试数学（理）试题）当时,不等式恒成立,则的取值范围为________.‎ ．（浙江省温州八校2013届高三9月期初联考数学（理）试题）已知函数,若恒成立,则实数的最小正值为___‎ ．（浙江省一级重点中学（六校）2013届高三第一次联考数学（理）试题）函数,函数,若存在,使得成立,则实数m的取值范围是 ______ .‎ ．（浙江省2013年高考模拟冲刺（提优）测试二数学（理）试题）函数的最小值是________;‎ ．（浙江省嘉兴市2013届高三第二次模拟考试理科数学试卷）将函数的图象先向左平移1个单位,再横坐标伸长为原来的2倍,则所得图象对应的函数解析式为____.‎ ．（浙江省诸暨中学2013届高三上学期期中考试数学（理）试题）已知,函数在上单调递减,则的取值范围是________‎ ．（浙江省温州中学2013届高三第三次模拟考试数学（理）试题）若函数的图象在上恰有一个极大值和一个极小值,‎ 则的取值范围是________. ‎ ．（浙江省温州十校联合体2013届高三期中考试数学（理）试题）已知直线与函数和函数的图象分别交于两点,若,则线段的中点纵坐标为_____.‎ ．（浙江省杭州市2013届高三上学期期中七校联考数学（理）试题）已知函数的图象的一部分如图3所示.则函数的解析式为__.‎ ．（浙江省杭州二中2013届高三6月适应性考试数学（理）试题）已知角的终边经过点,函数图象的相邻两条对称轴之间的距离等于,则=___________.‎ 三、解答题 ．（浙江省金华十校2013届高三4月模拟考试数学（理）试题）己知函数三个内角A,B,C的对边分别为a,b,c,且 ‎(I)求角B的大小;‎ ‎(II)若,求c的值.‎ ．（2013届浙江省高考压轴卷数学理试题）已知函数的最大值为2.‎ ‎(1)求函数在上的单调递减区间;‎ ‎(2)△ABC中,,角A、B、C所对的边分别是a、b、c,且C=60°,c=3,求△ABC的面积.‎ ．（浙江省宁波市鄞州中学2012学年高三第六次月考数学（理）试卷 ）已知函数.‎ ‎(1)若函数的图象关于点对称,且,求的值;‎ ‎(2)设,若是的充分条件,求实数的取值范围.‎ ．（浙江省考试院2013届高三上学期测试数学（理）试题）已知函数f (x)=3 sin2 ax+sin ax cos ax+2 cos2 ax的周期为π,其中a>0.‎ ‎(Ⅰ) 求a的值;‎ ‎(Ⅱ) 求f (x)的值域.‎ ．（浙江省温州市十校联合体2013届高三上学期期末联考理科数学试卷）函数的最小正周期是8‎ ‎(Ⅰ)求的值及函数的值域;‎ ‎(Ⅱ)若,且,求的值.‎ ．（浙江省重点中学协作体2013届高三摸底测试数学（理）试题）设函数,图像的一条对称轴是直线.‎ ‎(Ⅰ)求及函数的单调增区间 ‎(Ⅱ)证明:直线于函数的图像不相切.‎ ．（浙江省温州十校联合体2013届高三期中考试数学（理）试题）已知锐角中的内角A,B,C的对边分别为,定义向量 ‎, 且.‎ ‎(1)求函数的单调递增区间;‎ ‎(2)如果,求的面积的最大值.‎ ．（浙江省十校联合体2013届高三上学期期初联考数学（理）试题）已知函数,.‎ ‎(1)设是函数的一个零点,求的值;‎ ‎(2)求函数的单调递增区间.‎ ．（浙江省宁波一中2013届高三12月月考数学（理）试题）已知函数 ‎(1)求函数的最小正周期和单调递增区间;‎ ‎(2)已知内角A,B,C的对边分别为,若向量共线,求的值.‎ ．（浙江省宁波市金兰合作组织2013届高三上学期期中联考数学（理）试题）已知向量,,设函数的图象关于直线 对称,其中,为常数,且. ‎ ‎(Ⅰ)求函数的最小正周期; ‎ ‎(Ⅱ)若的图象经过点,求函数在区间上的取值范围.‎ ．（浙江省杭州二中2013届高三6月适应性考试数学（理）试题）已知函数.其图象的两个相邻对称中心的距离为,且过点.‎ ‎( Ⅰ) 函数的表达式;‎ ‎(Ⅱ)在中,分别是角的对边,,,角为锐角,且满足,求的值.‎ 浙江省2014届理科数学专题复习试题选编17：三角函数的图象与性质参考答案 一、选择题 D解: ‎ ‎ ‎ ‎ ‎ C ‎ C ‎ A ‎ D ‎ 解:由题意得是一条对称轴,故, ‎ 则,选 ‎ A ‎ C ‎ B ‎ D ‎ C ‎ C ‎ A ‎ D ‎ B ‎ D ‎ 解析:设,,则,, ‎ ‎,,,因为,故 ‎ 即,即,故. ‎ A选项:假设,则有:,即,无解. ‎ B选项:假设,则有:,即,无解. ‎ C选项:假设,则有:,即 ‎ ‎,无解.[来源:Z|xx|k.Com] ‎ D选项:假设,则有:,令,则 ‎ ‎,又,,故必存在使得:,故可能重合.D选项正确 ‎ B ‎ B ‎ B ‎ B ‎ B ‎ D ‎ B ‎ D.‎ D ‎ A.如图,函数与图象均点过的,且均关于点对称.∴零点关于“对称”,∵当时,所有零点和为9,∴此时,函数与图象有三个公共点,此时,,得.当时,且,∴有5个零点,且. ‎ D ‎ C ‎ B ‎ C ‎ 二、填空题 12 ‎ 1 ‎ ‎ 9个 ‎ ‎ ‎ ‎ ‎ ; ‎ ‎ ‎ ‎ ‎ ‎ 三、解答题 ‎ ‎ ‎ 【解析】(1)由题意,的最大值为,所以. ‎ 而,于是,. ‎ 为递减函数,则满足 , ‎ 即. ‎ 所以在上的单调递减区间为. ‎ ‎(2)设△ABC的外接圆半径为,由题意,得. ‎ 化简,得 ‎ ‎. ‎ 由正弦定理,得,. ① ‎ 由余弦定理,得,即. ② ‎ 将①式代入②,得. ‎ 解得,或 (舍去). ‎ ‎. ‎ ‎ 本题主要考查三角函数的图象与性质、三角变换等基础知识,同时考查运算求解能力.满分14分. ‎ ‎(Ⅰ) 由题意得 ‎ f (x)=(1-cos 2ax)+sin 2ax+(1+cos 2ax) ‎ ‎=sin 2ax-cos 2ax+ ‎ ‎=sin (2ax-)+. ‎ 因为f (x)的周期为π,a>0,所以 ‎ a=1. ‎ ‎(Ⅱ) 由(Ⅰ)得 ‎ f (x)=sin (2x-)+, ‎ 所以f (x)的值域为[,]. ‎ (Ⅰ)由已知可得: ‎ ‎=3cosωx+ ‎ 函数 ‎ 所以,函数 ‎ ‎(Ⅱ)因为(Ⅰ)有 ‎ ‎ ‎ 由x0 ‎ 所以, ‎ 故 ‎ ‎ ‎ ‎ ‎ 本题主要考查三角函数等基础知识,同时考查运算求解能力.满分14分. ‎ 解:(Ⅰ)∵是函数y=f(x)的图象的对称轴, ‎ ‎∴,∴, ‎ ‎∵,∴ ‎ ‎∴. ‎ 由题意得, ‎ 所以函数的单调增区间为 ‎ ‎(Ⅱ)证明:∵||=|(|=||≤2 ‎ 所以曲线y=f(x)的切线的斜率取值范围是[-2,2], ‎ 而直线5x-2y+c=0的斜率为>2, ‎ 所以直线5x-2y+c=0与函数的图象不相切 ‎ ‎ ‎ ‎ 又为锐角 故 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎∴函数的单调递增区间是 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 当, ‎ 即()时,[来源X.X .K ] ‎ 函数是增函数, ‎ 故函数的单调递增区间是() ‎ (1)f(x)=2sin(2x+)+1 ‎ 最小正周期T=,递增区间为 ‎ ‎(2)f(C)=2sin(‎2C+)+1=2, ,因为向量共线, ‎ 所以sinB=2sinA,,b=‎2a,由余弦定理可得 ‎ ‎ 解:(Ⅰ). ‎ 两个相邻对称中心的距离为,则, 又过点, ‎ ‎ ‎ ‎. ‎ ‎(Ⅱ),, ‎ ‎,又, ‎ 由余弦定理得,. ‎