高考数学复习专题练习选修4-1 第1讲 相似三角形的判定及有关性质

高考数学复习专题练习选修4-1 第1讲 相似三角形的判定及有关性质

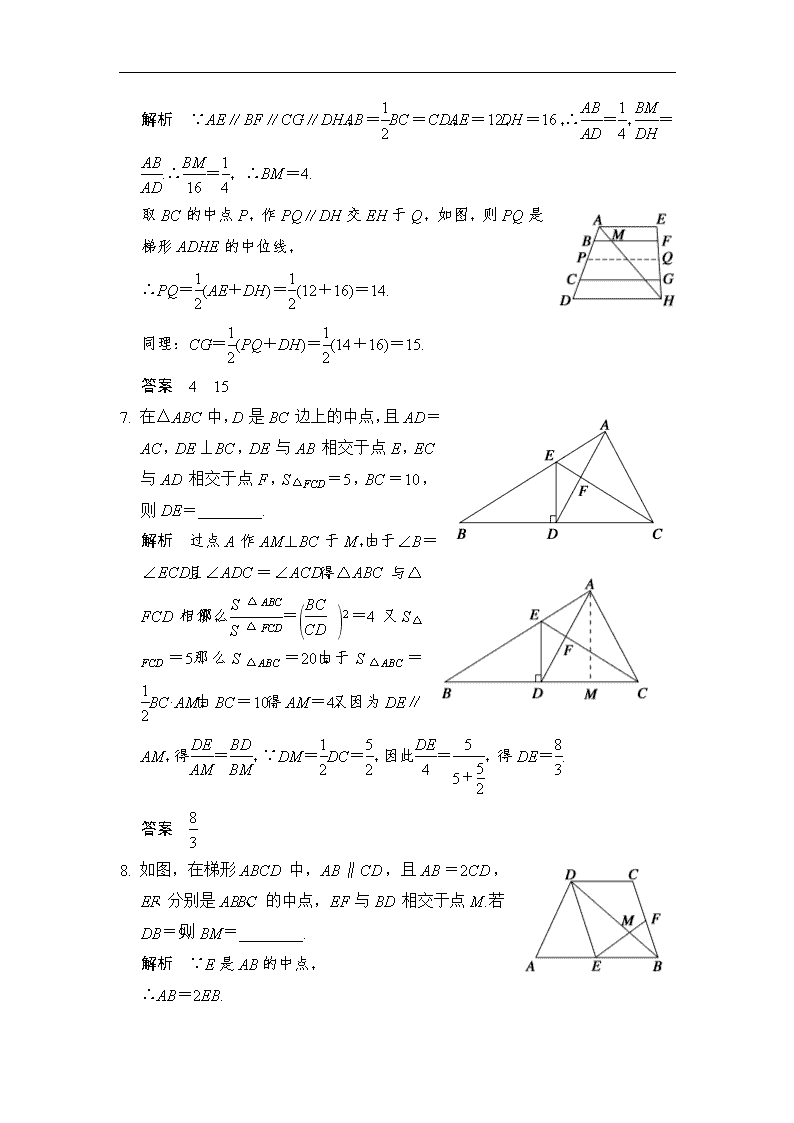
选修4-1 几何证明选讲 第1讲 相似三角形的判定及有关性质 一、填空题 ‎ ‎1. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，AD＝4，sin∠ACD＝，则CD＝________，BC＝________.‎ 解析　在Rt△ADC中，AD＝4，sin∠ACD＝＝，得 AC＝5，CD＝＝3，‎ 又由射影定理AC2＝AD·AB，得AB＝＝.‎ ‎∴BD＝AB－AD＝－4＝，‎ 由射影定理BC2＝BD·AB＝×，∴BC＝.‎ 答案　3　 ‎2. 如图，BD⊥AE，∠C＝90°，AB＝4，BC＝2，AD＝3，则EC＝________.‎ 解析　在Rt△ADB中，‎ DB＝＝，‎ 依题意得，△ADB∽△ACE，‎ ‎∴＝，可得EC＝＝2.‎ 答案　2 ‎3. 如图，已知AB∥EF∥CD，若AB＝4，CD＝12，则EF＝________.‎ 解析　∵AB∥CD∥EF，‎ ‎∴＝，＝，‎ ‎∴＝，＝，‎ ‎∴4(BC－BF)＝12BF，∴BC＝4BF，‎ ‎∴＝＝，∴EF＝3.‎ 答案　3‎ ‎4. 如图，在△ABC中，D是AC的中点，E是BD的中点，AE交于BC于F，则＝________.‎ 解析　如图，过点D作DG∥AF，交BC于点G，易得FG＝GC，又在三角形BDG中，BE＝DE，即EF为三角形BDG的中位线，故BF＝FG，因此＝.‎ 答案　 ‎5. 如图，∠C＝90°，∠A＝30°，E是AB中点，DE⊥AB于E，则△ADE与△ABC的相似比是________．‎ 解析　∵E为AB中点，∴＝，即AE＝AB，‎ 在Rt△ABC中，∠A＝30°，AC＝AB，‎ 又∵Rt△AED∽Rt△ACB，∴相似比为＝.‎ 故△ADE与△ABC的相似比为1∶.‎ 答案　1∶ ‎6. 如图，AE∥BF∥CG∥DH，AB＝BC＝CD，AE＝12，DH＝16，AH交BF于M，则BM＝________，CG＝________.‎ 解析　∵AE∥BF∥CG∥DH，AB＝BC＝CD，AE＝12，‎ DH＝16，∴＝，＝.∴＝，∴BM＝4.‎ 取BC的中点P，作PQ∥DH交EH于Q，如图，则PQ是梯形ADHE的中位线，‎ ‎∴PQ＝(AE＋DH)＝(12＋16)＝14.‎ 同理：CG＝(PQ＋DH)＝(14＋16)＝15.‎ 答案　4　15‎ ‎7. 在△ABC中，D是BC边上的中点，且AD＝AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F，S△FCD＝5，BC＝10，则DE＝________.‎ 解析　过点A作AM⊥BC于M，由于∠B＝∠ECD，且∠ADC＝∠ACD，得△ABC与△FCD相似，那么＝2＝4又S△FCD＝5，那么S△ABC＝20，由于S△ABC＝BC·AM，由BC＝10，得AM＝4，又因为DE∥AM，得＝，∵DM＝DC＝，因此＝，得DE＝.‎ 答案　 ‎8. 如图，在梯形ABCD中，AB∥CD，且AB＝2CD，E、F分别是AB、BC的中点，EF与BD相交于点M.若DB＝9，则BM＝________.‎ 解析　∵E是AB的中点，‎ ‎∴AB＝2EB.‎ ‎∵AB＝2CD，∴CD＝EB.‎ 又AB∥CD，∴四边形CBED是平行四边形．‎ ‎∴CB∥DE，∴ ‎∴△EDM∽△FBM.∴＝.‎ ‎∵F是BC的中点，∴DE＝2BF.‎ ‎∴DM＝2BM.∴BM＝DB＝3.‎ 答案　3‎ 二、解答题 ‎9．如图，在等腰梯形ABCD中，AD∥BC，AB＝DC，过点D作AC的平行线DE，交BA的延长线于点E，求证：‎ ‎(1)△ABC≌△DCB；‎ ‎(2)DE·DC＝AE·BD.‎ 证明　(1)∵四边形ABCD是等腰梯形，∴AC＝BD.‎ ‎∵AB＝DC，BC＝CB，∴△ABC≌△DCB.‎ ‎(2)∵△ABC≌△DCB.‎ ‎∴∠ACB＝∠DBC，∠ABC＝∠DCB.‎ ‎∵AD∥BC，∴∠DAC＝∠ACB，∠EAD＝∠ABC.‎ ‎∴∠DAC＝∠DBC，∠EAD＝∠DCB.‎ ‎∵ED∥AC，∴∠EDA＝∠DAC.‎ ‎∴∠EDA＝∠DBC，∴△ADE∽△CBD.‎ ‎∴DE∶BD＝AE∶CD.‎ ‎∴DE·DC＝AE·BD.‎ ‎10．如图，△ABC中，AB＝AC，∠BAC＝90°，AE＝AC，BD＝AB，点F在BC上，且CF＝BC.求证：‎ ‎(1)EF⊥BC；‎ ‎(2)∠ADE＝∠EBC.‎ 证明　设AB＝AC＝‎3a，则AE＝BD＝a，CF＝a.‎ ‎(1)＝＝，＝＝ 又∠C为公共角，故△BAC∽△EFC，由∠BAC＝90°.‎ ‎∴∠EFC＝90°，∴EF⊥BC.‎ ‎(2)由(1)得EF＝a，‎ 故＝＝，＝＝，‎ ‎∴＝.∵∠DAE＝∠BFE＝90°，‎ ‎∴△ADE∽△FBE，‎ ‎∴∠ADE＝∠EBC.‎