高考数学复习选择题、填空题70分练(四)
选择题、填空题70分练(四)
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2014·惠州模拟)设两集合A={x|y=ln(1-x)},B={y|y=x2},则用阴影部分表示A∩B正确的是 ( )
【解析】选A.A={x|y=ln(1-x)}=(-∞,1),B={y|y=x2}=[0,+∞),A∩B=[0,1),故选A.
2.已知i为虚数单位,复数z=,则|z|+= ( )
A.i B.1-i
C.1+i D.-i
【解析】选B.由已知得z====i,|z|+=|i|+=1-i.
【加固训练】设复数x=,则|x+i|= ( )
A.1 B. C. D.
【解析】选D.因为x===-1+i,
则|x+i|=|-1+2i|==.
3.(2014·茂名模拟)已知命题p:x0∈R,x0-2>lgx0,命题q:x∈R,x2>0,则
( )
A.命题p∨q是假命题
B.命题p∧q是真命题
C.命题p∨(q)是假命题
D.命题p∧(q)是真命题
【解析】选D.对于命题p:x0∈R,x0-2>lgx0,利用特殊值可知,当x0=3时,x0-2=1,而lgx0=lg3
lgx0,即x0∈R,x0-2>lgx0,所以命题p是真命题;对于命题q:x∈R,x2>0,可知当x=0时,x2=0,所以命题q为假命题,则q为真命题,故命题p∧(q)是真命题.
4.若两个正实数x,y满足+=1,并且x+2y>m2+2m恒成立,则实数m的取值范围是
( )
A.(-∞,-2)∪[4,+∞)
B.(-∞,-4]∪[2,+∞)
C.(-2,4)
D.(-4,2)
【解析】选D.x+2y=(x+2y)=2+++2≥8,当且仅当=,即4y2=x2时等号成立.x+2y>m2+2m恒成立,则m2+2m<8,m2+2m-8<0,解得-40),练车时间为t,则函数θ=f(t)的图象大致为 ( )
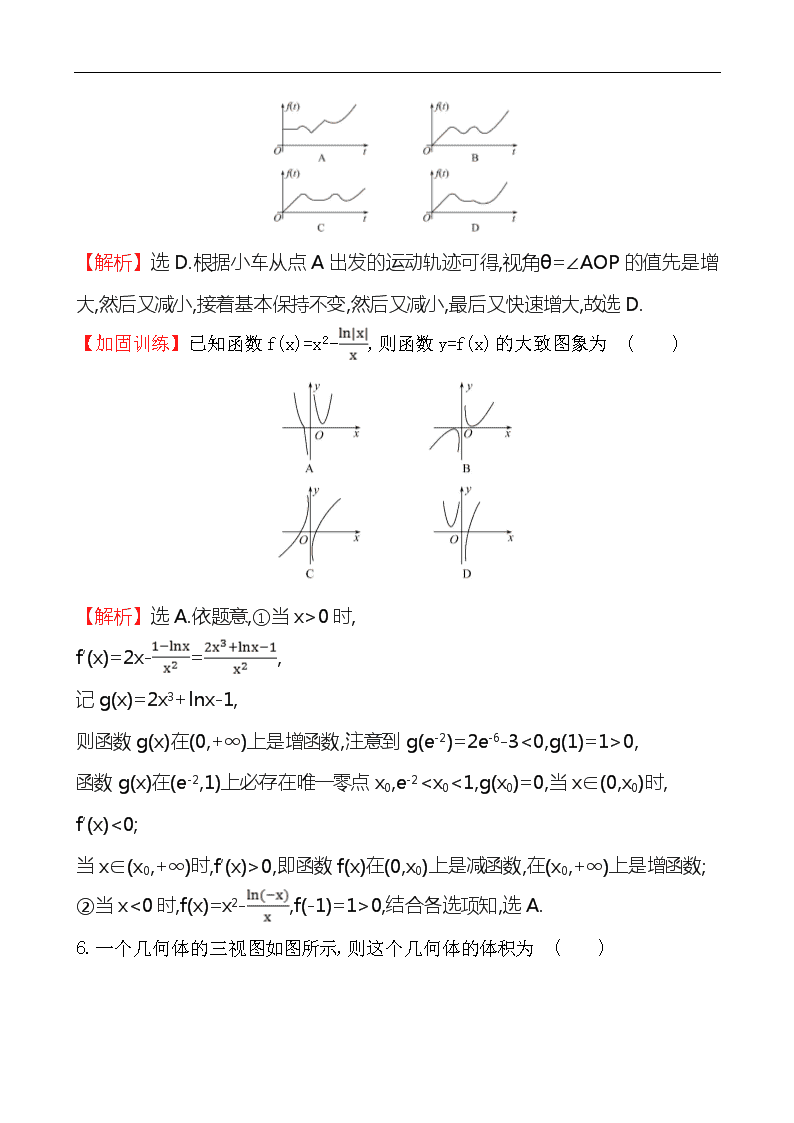
【解析】选D.根据小车从点A出发的运动轨迹可得,视角θ=∠AOP的值先是增大,然后又减小,接着基本保持不变,然后又减小,最后又快速增大,故选D.
【加固训练】已知函数f(x)=x2-,则函数y=f(x)的大致图象为 ( )
【解析】选A.依题意,①当x>0时,
f′(x)=2x-=,
记g(x)=2x3+lnx-1,
则函数g(x)在(0,+∞)上是增函数,注意到g(e-2)=2e-6-3<0,g(1)=1>0,
函数g(x)在(e-2,1)上必存在唯一零点x0,e-20,即函数f(x)在(0,x0)上是减函数,在(x0,+∞)上是增函数;
②当x<0时,f(x)=x2-,f(-1)=1>0,结合各选项知,选A.
6.一个几何体的三视图如图所示,则这个几何体的体积为 ( )
A. B.
C. D.
【解析】选A.该几何体由底面半径为1的半圆锥与底面为边长等于2的正方形的四棱锥组成,且高都为,因此该几何体的体积为V=××+×(2×2)×=+=.
【加固训练】一个几何体的三视图如图所示,则该几何体的表面积为 .
【解析】由三视图可知,该几何体是一个长方体中间挖去一个圆柱,其中长方体的长、宽、高分别是4,3,1,中间被挖去的是底面半径为1,母线长为1的圆柱,所以几何体的表面积等于长方体的表面积减去圆柱两个底面的面积,再加上圆柱的侧面积,即为2×(4×3+4×1+3×1)-2π+2π=38.
答案:38
7.(2014·三明模拟)已知函数y=f(x)是定义在R上且以3为周期的奇函数,当x∈时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为 ( )
A.3 B.5 C.7 D.9
【解析】选C.当x∈时,-x∈,f(x)=-f(-x)=-ln(x2+x+1);则f(x)在区间上有3个零点(在区间上有2个零点).根据函数周期性,可得f(x)在上也有3个零点,在上有2个零点.故函数f(x)在区间[0,6]上一共有7个零点.
8.数列{an}的通项an=n2,其前n项和为Sn,则S30为 ( )
A.470 B.490 C.495 D.510
【解析】选A.注意到an=n2cos,且函数y=cos的最小正周期是3,因此当n是正整数时,an+an+1+an+2=-n2-(n+1)2+(n+2)2=3n+,其中
n=1,4,7…,S30=(a1+a2+a3)+(a4+a5+a6)+…+(a28+a29+a30)=
++…+=3×+×10=470.
二、填空题(本大题共6小题,每小题5分,共30分.把答案填在题中横线上)
9.执行如图所示的程序框图,则输出的n的值为 .
【解析】执行程序框图可知:n=1,s=0,p=30,s0,b>0),则+=·(a+b)=5++≥5+4=9,当且仅当=,即b=2a时等号成立.
答案:9
【加固训练】若直线l被圆x2+y2=4所截得的弦长为2,则l与曲线+y2=1的公共点个数为( )
A.1个 B.2个
C.1个或2个 D.1个或0个
【解析】选C.①若直线l的斜率不存在,则直线l的方程为x=1或x=-1,此时直线l与曲线+y2=1有两个公共点;
②若直线l的斜率存在,不妨设直线l的方程为y=kx+b,因为直线l被圆x2+y2=4所截得的弦长为2,
所以b2=k2+1,
联立直线方程与曲线方程:
消y得:x2+6kbx+3b2-3=0,
所以Δ=36k2b2-4=24k2≥0,
所以l与曲线+y2=1的公共点个数为1个或2个.
11.已知抛物线x2=4y上有一条长为6的动弦AB,则AB的中点到x轴的最短距离为 .
【解析】由题意知,抛物线的准线l:y=-1,过A作AA1⊥l于A1,过B作BB1⊥l于B1.设弦AB的中点为M,过M作MM1⊥l于M1,则|MM1|=.|AB|≤|AF|+|BF|(F为抛物线的焦点),即|AF|+|BF|≥6,|AA1|+|BB1|≥6,2|MM1|≥6,|MM1|≥3,故M到x轴的距离d≥2.
答案:2
12.(2014·珠海模拟)在平面直角坐标系中,若不等式组(a为常数)所表示的平面区域的面积等于2,则a的值为 .
【解析】不等式组所围成的区域如图所示.
则A(1,0),B(0,1),C(1,1+a),
且a>-1,因为S△ABC=2,
所以(1+a)×1=2,解得a=3.
答案:3
13.若向量a=(cosθ,sinθ),b=(,-1),则|2a-b|的最大值为 .
【解析】因为向量a=(cosθ,sinθ),b=(,-1),
所以|a|=1,|b|=2,a·b=cosθ-sinθ,
所以|2 a- b|2=4a2+b2-4a·b
=8-4=8-8cos,
所以|2 a- b|2的最大值为16,
因此|2a-b|的最大值为4.
答案:4
【加固训练】已知向量a=(x,-2),b=(y,1),其中x,y都是正实数,若a⊥b,则t=x+2y的最小值是 .
【解析】由a⊥b可得a·b=0,
即xy-2=0,故xy=2.
由于t=x+2y≥2=4,
当且仅当x=2y时等号成立,故t的最小值为4.
答案:4
14.(2014·泰安模拟)设f(x)是定义在R上的函数,满足f(x+2)=-f(x),且x∈[0,2]时,f(x)=2x-x2.则x∈[-2,0]时,f(x)= .
【解析】因为x∈[-2,0],
则x+2∈[0,2],
所以f(x)=-f(x+2)=-[2(x+2)-(x+2)2],
即x∈[-2,0]时,f(x)=x2+2x.
答案:x2+2x
关闭Word文档返回原板块