- 2021-06-25 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013年普通高等学校招生全国统一考试数学理试题(北京卷)
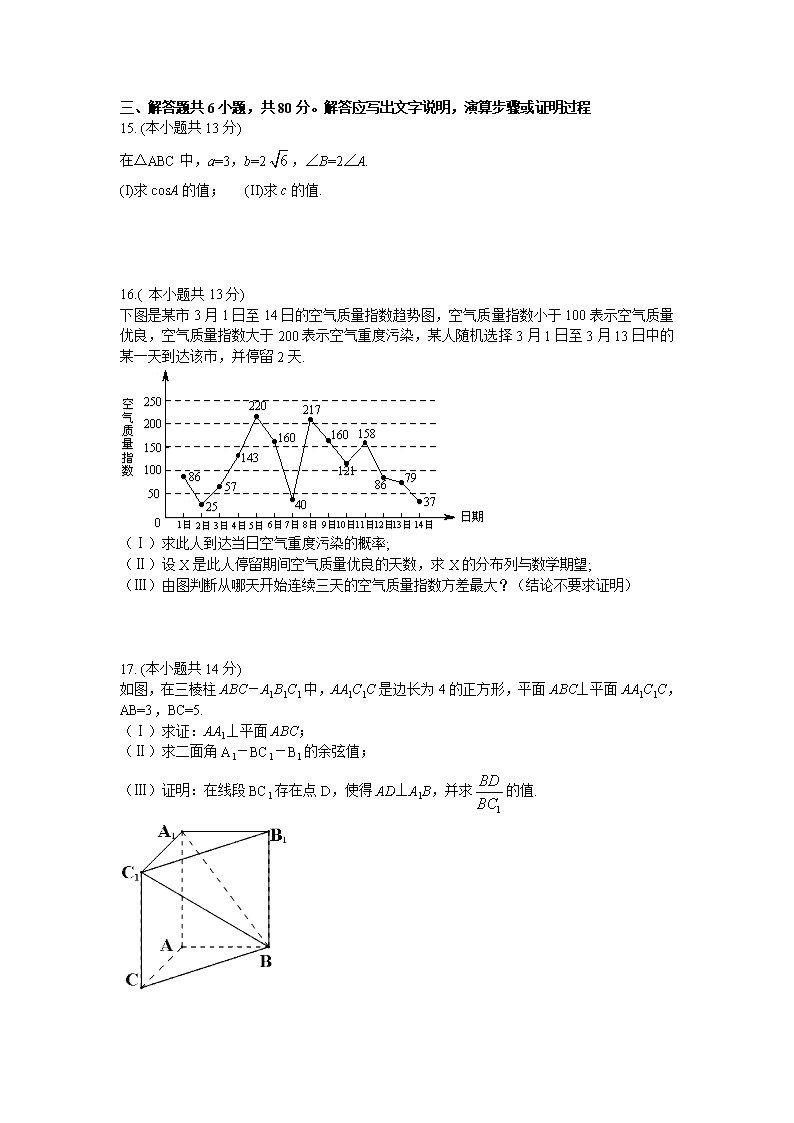
2013北京高考理科数学试题 第一部分 (选择题 共40分) 一、 选择题共8小题。每小题5分,共40分。在每个小题给出的四个选项中,只有一项是符合题目要求的一项。 1.已知集合A={-1,0,1},B={x|-1≤ x<1},则A∩B= ( ) A.{0} B.{-1,0} C.{0,1} D.{-1,0,1} 2.在复平面内,复数(2-i)2对应的点位于( ) A.第一象限 B. 第二象限 C.第三象限 D. 第四象限 3.“φ=π”是“曲线y=sin(2x+φ)过坐标原点的” A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 4.执行如图所示的程序框图,输出的S值为 开始 是 否 输出 结束 A.1 B. C. D. 5.函数f(x)的图象向右平移1个单位长度,所得图象与y=ex关于y轴对称,则f(x)= A. B. C. D. 6.若双曲线的离心率为,则其渐近线方程为 A.y=±2x B.y= C. D. 7.直线l过抛物线C: x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于 A. B.2 C. D. 8.设关于x,y的不等式组表示的平面区域内存在点P(x0,y0),满足x0-2y0=2,求得m的取值范围是 A. B. C. D. 第二部分(非选择题 共110分) 二、填空题共6题,每小题5分,共30分. 9.在极坐标系中,点(2,)到直线ρsinθ=2的距离等于 . 10.若等比数列{an}满足a2+a4=20,a3+a5=40,则公比q= ;前n项和Sn= . 11.如图,AB为圆O的直径,PA为圆O的切线,PB与圆O相交于D.若PA=3,,则PD= ;AB= . 12.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是 . 13.向量a,b,c在正方形网格中的位置如图所示.若c=λa+μb (λ,μ∈R),则= . 14.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为 . 三、解答题共6小题,共80分。解答应写出文字说明,演算步骤或证明过程 15. (本小题共13分) 在△ABC中,a=3,b=2,∠B=2∠A. (I)求cosA的值; (II)求c的值. 16.( 本小题共13分) 下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天. (Ⅰ)求此人到达当日空气重度污染的概率; (Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望; (Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明) 17. (本小题共14分) 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5. (Ⅰ)求证:AA1⊥平面ABC; (Ⅱ)求二面角A1-BC1-B1的余弦值; (Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求的值. 18. (本小题共13分) 设L为曲线C:在点(1,0)处的切线. (I)求L的方程; (II)证明:除切点(1,0)之外,曲线C在直线L的下方. 19. (本小题共14分) 已知A、B、C是椭圆W:上的三个点,O是坐标原点. (I)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积; (II)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由. 20. (本小题共13分) 已知{an}是由非负整数组成的无穷数列,该数列前n项的最大值记为An,第n项之后各项,,…的最小值记为Bn,dn=An-Bn 。 (I)若{an}为2,1,4,3,2,1,4,3,…,是一个周期为4的数列(即对任意n∈N*,),写出d1,d2,d3,d4的值; (II)设d为非负整数,证明:dn=-d(n=1,2,3…)的充分必要条件为{an}为公差为d的等差数列; (III)证明:若a1=2,dn=1(n=1,2,3,…),则{an}的项只能是1或者2,且有无穷多项为1. 参考答案 一、 选择题: 1.B 2.D 3.A 4.C 5.D 6.B 7.C 8.C 二、填空题: 9.1 10.2, 11. ;4 12.96 13.4 14. 三.解答题: 15.解:(I)因为a=3,b=2,∠B=2∠A. 所以在△ABC中,由正弦定理得.所以.故. (II)由(I)知,所以.又因为∠B=2∠A,所以.所以. 在△ABC中,. 所以. 16.解:设表示事件“此人于3月日到达该市”( =1,2,…,13). 根据题意, ,且. (I)设B为事件“此人到达当日空气重度污染”,则, 所以. (II)由题意可知,X的所有可能取值为0,1,2,且 P(X=1)=P(A3∪A6∪A7∪A11)= P(A3)+P(A6)+P(A7)+P(A11)= , P(X=2)=P(A1∪A2∪A12∪A13)= P(A1)+P(A2)+P(A12)+P(A13)= , P(X=0)=1-P(X=1)-P(X=2)= , 所以X的分布列为: 故X的期望. (III)从3月5日开始连续三天的空气质量指数方差最大. 17.解: (I)因为AA1C1C为正方形,所以AA1 ⊥AC. 因为平面ABC⊥平面AA1C1C,且AA1垂直于这两个平面的交线AC,所以AA1⊥平面ABC. (II)由(I)知AA1 ⊥AC,AA1 ⊥AB. 由题知AB=3,BC=5,AC=4,所以AB⊥AC. 如图,以A为原点建立空间直角坐标系A-,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4), 设平面A1BC1的法向量为,则,即, 令,则,,所以. 同理可得,平面BB1C1的法向量为,所以. 由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为. (III)设D是直线BC1上一点,且. 所以.解得,,. 所以. 由,即.解得. 因为,所以在线段BC1上存在点D, 使得AD⊥A1B. 此时,. 18.解: (I)设,则.所以.所以L的方程为. (II)令,则除切点之外,曲线C在直线的下方等价于 . 满足,且. 当时,,,所以,故单调递减; 当时,,,所以,故单调递增. 所以,(). 所以除切点之外,曲线C在直线L的下方. 又解:即变形为,记,则, 所以当时,,在(0,1)上单调递减; 当时,,在(1,+∞)上单调递增。 所以.) 19.解:(I)椭圆W:的右顶点B的坐标为(2,0).因为四边形OABC为菱形,所以AC与OB相互垂直平分. 所以可设A(1,),代入椭圆方程得,即. 所以菱形OABC的面积是. (II)假设四边形OABC为菱形. 因为点B不是W的顶点,且直线AC不过原点,所以可设AC的方程为. 由消去并整理得. 设A,C,则,. 所以AC的中点为M(,). 因为M为AC和OB的交点,所以直线OB的斜率为. 因为,所以AC与OB不垂直. 所以OABC不是菱形,与假设矛盾. 所以当点B不是W的顶点时,四边形OABC不可能是菱形. 20.(I) (II)(充分性)因为是公差为的等差数列,且,所以 因此,,. (必要性)因为,所以. 又因为,,所以. 于是,. 因此,即是公差为的等差数列. (III)因为,所以,.故对任意. 假设中存在大于2的项. 设为满足的最小正整数,则,并且对任意,. 又因为,所以,且. 于是,. 故,与矛盾. 所以对于任意,有,即非负整数列的各项只能为1或2. 因此对任意,,所以. 故. 因此对于任意正整数,存在满足,且,即数列有无穷多项为1. 查看更多