高考数学专题复习教案： 算法与程序框图备考策略

高考数学专题复习教案： 算法与程序框图备考策略

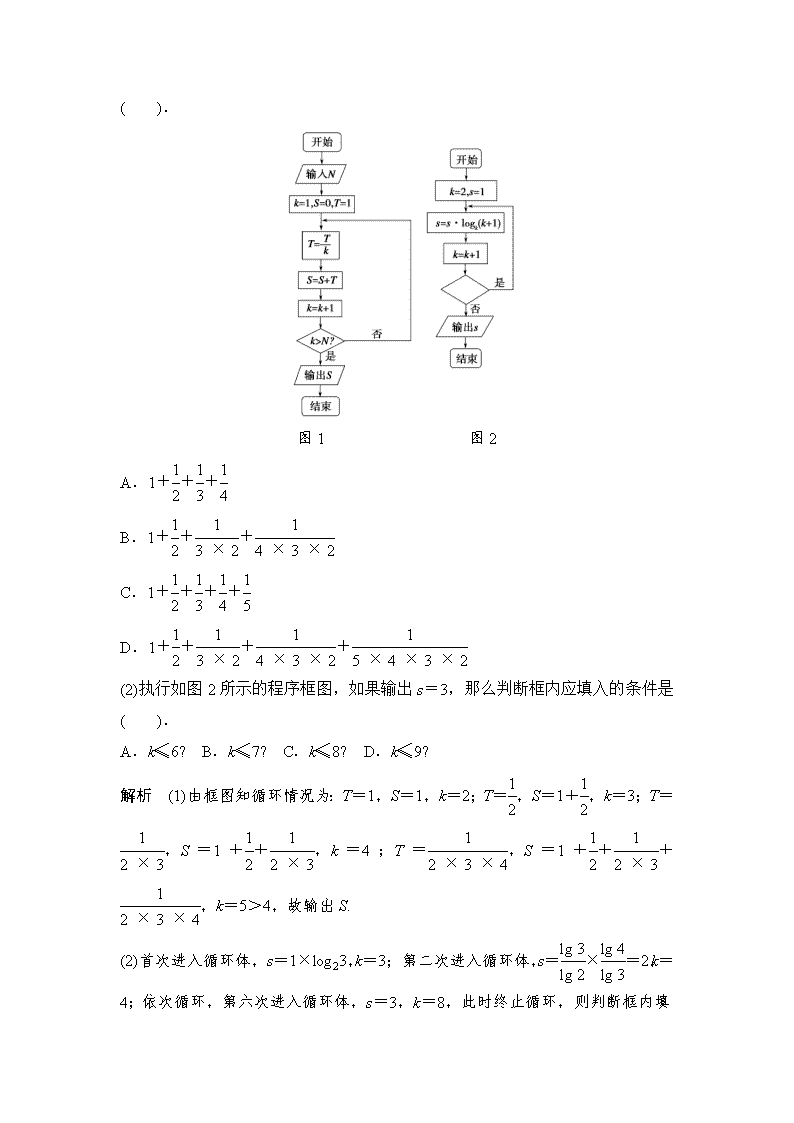
算法与程序框图备考策略 主标题：算法与程序框图备考策略 副标题：通过考点分析高考命题方向，把握高考规律，为学生备考复习打通快速通道。 关键词：算法，框图，备考策略 难度：2 重要程度：4 内容 考点一　基本逻辑结构 【例 1】 (1)某程序框图如图所示，若该程序运行后输出的值是9 5 ，则(　　)． A．a＝4 B．a＝5 C．a＝6 D．a＝7 (2) 执 行 下 面 的 程 序 框 图 ， 若 输 入 的 ε 的 值 为 0.25 ， 则 输 出 的 n 的 值 为 ________． 解析　(1)依框图知：当 k＞a 时，S＝1＋ 1 1 × 2 ＋ 1 2 × 3 ＋…＋ 1 k(k＋1)＝1＋ (1 1 －1 2)＋(1 2 －1 3)＋…＋(1 k － 1 k＋1)＝1＋1－1 2 ＋1 2 －1 3 ＋…＋1 k － 1 k＋1 ＝2－ 1 k＋1.当 S＝9 5 时，k＝4，故由程序框图可知 k＝4＞a 不成立，k＝5＞a 成立，所以 a＝4. (2)由程序框图可知： 第一次运行：F1＝1＋2＝3，F0＝3－1＝2，n＝1＋1＝2， 1 F1 ＝1 3 ＞ε，不满足要求， 继续运行； 第二次运行：F1＝2＋3＝5，F0＝5－2＝3，n＝2＋1＝3， 1 F1 ＝1 5 ＝0.2＜ε，满足条 件． 结束运行，输出 n＝3. 答案　(1)A　(2)3 【备考策略】 此类问题的一般解法是严格按照程序框图设计的计算步骤逐步计 算，逐次判断是否满足判断框内的条件，决定循环是否结束．要注意初始值的变 化，分清计数变量与累加(乘)变量，掌握循环体等关键环节． 考点二　程序框图的识别与应用问题 【例 2】 (1)执行如图 1 的程序框图，如果输入的 N＝4，那么输出的 S＝ (　　)． 图 1　　　　　　　　　图 2 A．1＋1 2 ＋1 3 ＋1 4 B．1＋1 2 ＋ 1 3 × 2 ＋ 1 4 × 3 × 2 C．1＋1 2 ＋1 3 ＋1 4 ＋1 5 D．1＋1 2 ＋ 1 3 × 2 ＋ 1 4 × 3 × 2 ＋ 1 5 × 4 × 3 × 2 (2)执行如图 2 所示的程序框图，如果输出 s＝3，那么判断框内应填入的条件是 (　　)． A．k≤6? B．k≤7? C．k≤8? D．k≤9? 解析　(1)由框图知循环情况为：T＝1，S＝1，k＝2；T＝1 2 ，S＝1＋1 2 ，k＝3；T＝ 1 2 × 3 ， S ＝ 1 ＋ 1 2 ＋ 1 2 × 3 ， k ＝ 4 ； T ＝ 1 2 × 3 × 4 ， S ＝ 1 ＋ 1 2 ＋ 1 2 × 3 ＋ 1 2 × 3 × 4 ，k＝5＞4，故输出 S. (2)首次进入循环体，s＝1×log23，k＝3；第二次进入循环体，s＝lg 3 lg 2 ×lg 4 lg 3 ＝2， k＝4；依次循环，第六次进入循环体，s＝3，k＝8，此时终止循环，则判断框内 填 k≤7？. 答案　(1)B　(2)B 【备考策略】 识别、运行程序框图和完善程序框图的思路 (1)要明确程序框图的顺序结构、条件结构和循环结构． (2)要识别、运行程序框图，理解框图所解决的实际问题． (3)按照题目的要求完成解答并验证． 考点三　基本算法语句 【例 3】 (1)根据图 1 算法语句，当输入 x 为 60 时，输出 y 的值为(　　)． 图 1　　　　　　　　　图 2 A．25 B．30 C．31 D．61 (2)根据图 2 的程序写出相应的算法功能为________． 解析　(1)通过阅读理解知，算法语句是一个分段函数 y＝f(x)＝Error! ∴y＝f(60)＝25＋0.6×(60－50)＝31. (2)该程序是计算 1～999 中连续奇数的平方和． 答案　(1)C　(2)求和：12＋32＋52＋…＋9992 【备考策略】 输入、输出和赋值语句是任何一个算法必不可少的语句，一个语句 可以输出多个表达式．在赋值语句中，一定要注意其格式的要求，如“＝”的右 侧必须是表达式，左侧必须是变量；一个语句只能给一个变量赋值；变量的值始 终等于最近一次赋给它的值，先前的值将被替换；条件语句的主要功能是实现算 法中的条件结构，解决像“判断一个数的正负”“比较两个数的大小”“对一组 数进行排序”“求分段函数的函数值”等问题，计算时就需要用到条件语句．