2018-2019学年内蒙古集宁一中(西校区)高一下学期期中考试数学（文）试题（解析版）

2018-2019学年内蒙古集宁一中(西校区)高一下学期期中考试数学（文）试题（解析版）

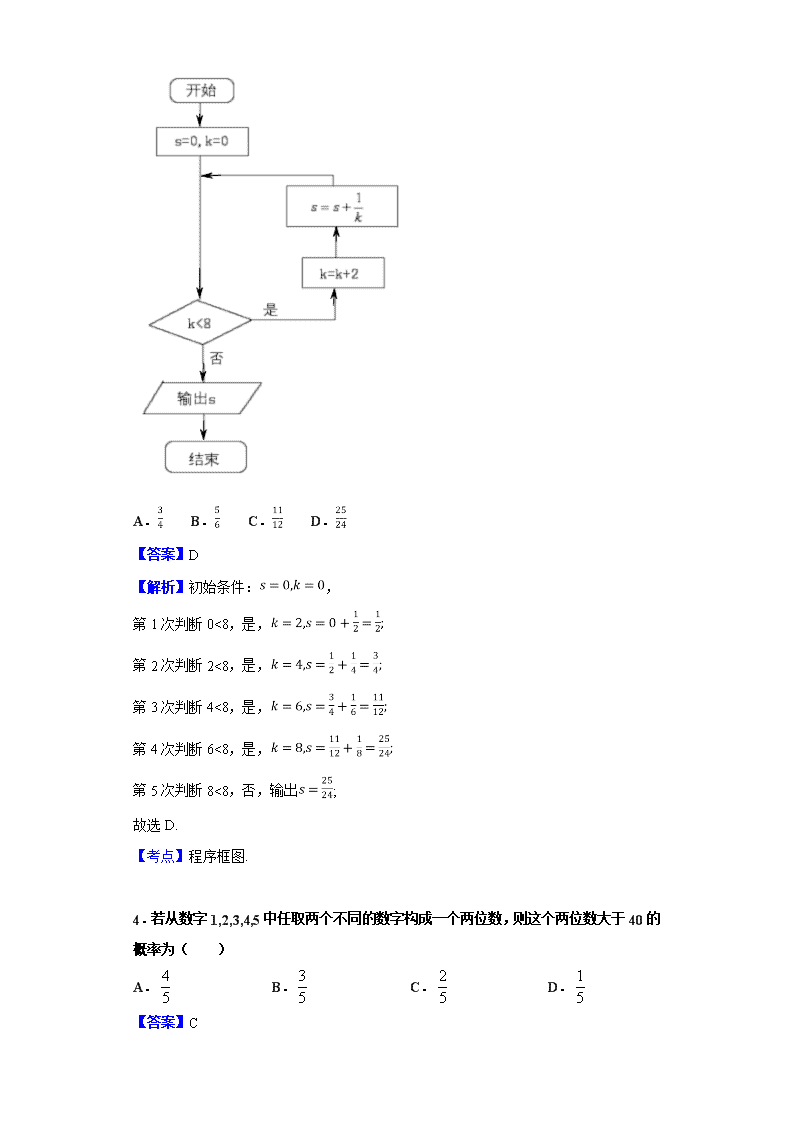
‎2018-2019学年内蒙古集宁一中(西校区)高一下学期期中考试数学（文）试题 一、单选题 ‎1．是（ ）‎ A．第一象限角 B．第二象限角 C．第三象限角 D．第四象限角 ‎【答案】B ‎【解析】由题意结合角的概念的推广即可确定角所在的象限.‎ ‎【详解】‎ 由于，而位于第二象限，‎ 故是第二象限角.‎ 故选：B.‎ ‎【点睛】‎ 本题主要考查角的概念的推广，角的终边所在象限的确定，属于基础题.‎ ‎2．某校高一年级某班共有名学生，现采用系统抽样的方法从中抽取名学生做“跑操与健康”的调查，为此将学生编号为，选取的这名学生的编号可能是（ ）‎ A． B．‎ C． D．‎ ‎【答案】B ‎【解析】分析：根据系统抽样的定义进行求解即可．‎ 详解：根据系统抽样的定义，从60名学生中抽取6名学生，编号的间隔为 ‎ ‎ ‎∴编号组成的数列应是公差为10的等差数列，‎ 故选：B．‎ 点睛! 本题主要考查系统抽样的应用，求出号码间隔是解决本题的关键．‎ ‎3．执行如图所示的程序框图，则输出s的值为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】初始条件：，‎ 第1次判断0<8，是，‎ 第2次判断2<8，是，‎ 第3次判断4<8，是，‎ 第4次判断6<8，是，‎ 第5次判断8<8，否，输出;‎ 故选D.‎ ‎【考点】程序框图.‎ ‎4．若从数字1,2,3,4,5中任取两个不同的数字构成一个两位数，则这个两位数大于40的概率为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】从数字1，2，3，4，5中任取两个不同的数字构成一个两位数，‎ 这个两位数大于40,则十位数字为4或5，共有.‎ 概率为.‎ 故选C.‎ 点睛：古典概型中基本事件数的探求方法 ‎(1)列举法.‎ ‎(2)树状图法：适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目，常采用树状图法.‎ ‎(3)列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化.‎ ‎(4)排列组合法：适用于限制条件较多且元素数目较多的题目.‎ ‎5．当圆的面积最大时，圆心坐标是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】先列圆面积解析式，再根据圆面积最大时k的值确定对应圆心坐标.‎ ‎【详解】‎ 因为，所以，‎ 因此圆面积为时圆面积最大，此时圆心坐标为，选B.‎ ‎【点睛】‎ 本题考查圆的标准方程，考查基本化简求解能力.‎ ‎6．集合中的角所表示的范围（阴影部分）是（ ）‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】考查k=0,1,2的情形即可确定角所表示的范围.‎ ‎【详解】‎ 当时，即，即选项C中第一象限所示的部分；‎ 当时，即，即选项C中第三象限所示的部分；‎ 当时，其所表示的角的范围与表示的范围一致.‎ 综上可得，选项C表示集合中的角所表示的范围.‎ 故选：C.‎ ‎【点睛】‎ 本题主要考查终边相同的角的表示，角所在位置的确定等知识，意在考查学生的转化能力和计算求解能力.‎ ‎7．直线与圆相切，则（ ）‎ A． B． C． D．2‎ ‎【答案】D ‎【解析】　圆心到直线距离，解得m＝2.选D.‎ ‎8．在一段时间内，某种商品的价格（元）和销售量（件）之间的一组数据如下表：‎ 价格（元）‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ 销售量（件）‎ ‎3‎ ‎5‎ ‎8‎ ‎9‎ ‎10‎ 若与呈线性相关关系，且解得回归直线的斜率，则的值为（ ）‎ A．0.2 B．-0.7 C．-0.2 D．0.7‎ ‎【答案】C ‎【解析】由题意利用线性回归方程的性质计算可得的值.‎ ‎【详解】‎ 由于，，‎ 由于线性回归方程过样本中心点，故：，‎ 据此可得：.‎ 故选：C.‎ ‎【点睛】‎ 本题主要考查线性回归方程的性质及其应用，属于中等题.‎ ‎9．已知直线的方程是，的方程是，则下列各图形中，正确的是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】对于D：l1:y=ax+b,l2:y=bx-a.由l1可知a<0,b<0,对应l2也符合,‎ ‎10．甲、乙两名同学在5次考试中的数学成绩用茎叶图表示如图所示。若甲、乙两人的平均成绩分别是，，则下列说法正确的是（ ）‎ A．甲比乙成绩稳定 B．，乙比甲成绩稳定 C．，甲比乙成绩稳定 D．，乙比甲成绩稳定 ‎【答案】D ‎【解析】试题分析：所以，乙比甲成绩稳定，选.‎ ‎【考点】1.茎叶图；2.平均数.‎ ‎11．已知圆的方程为，是该圆内一点，过点P的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎，最长的弦长为直径，‎ 最短的弦长是过且与直径垂直的弦长，‎ 四边形的面积为 故答案选 点睛：根据题意，为经过点的圆的直径， 而是与垂直的弦，因此算出的长，利用垂直于弦的直径的性质算出长，根据四边形的面积公式，即可算出四边形的面积。‎ 二、填空题 ‎12．如果对任何实数k，直线都过一个定点A，那么点A的坐标是______.‎ ‎【答案】‎ ‎【解析】试题分析：方法一：一般取任意两个值，解二元一次方程就可以了.但是取合适的值会使计算简化，一般使一个未知数的系数为.取，方程就是，；取，方程就是，；所以点的坐标是；将点坐标代入方程得：，所以直线恒经过点；方法二：是将当做未知数，将方程写成，对于任意值，等式成立，所以，；解得，所以点的坐标是.故答案为：.‎ ‎【考点】直线过定点问题.‎ ‎13．在区间上随机取一个数x，则的概率为_________‎ ‎【答案】‎ ‎【解析】分析：直接利用几何概型求解.‎ 详解：因为|x|≤1，所以-1≤x≤1，所以的概率为.故答案为：‎ 点睛：（1）本题主要考查几何概型的计算，意在考查学生对几何概型的掌握水平.(2) 几何概型的解题步骤:首先是判断事件是一维问题还是二维、三维问题（事件的结果与一个变量有关就是一维的问题，与两个变量有关就是二维的问题，与三个变量有关就是三维的问题）；接着，如果是一维的问题，先确定试验的全部结果和事件构成的区域长度（角度、弧长等），最后代公式；如果是二维、三维的问题，先设出二维或三维变量，再列出试验的全部结果和事件分别满足的约束条件，作出两个区域，最后计算两个区域的面积或体积代公式.‎ ‎14．弧长为，圆心角为的扇形，其面积为____.‎ ‎【答案】‎ ‎【解析】首先求得半径，然后利用面积公式求面积即可.‎ ‎【详解】‎ 设扇形半径为，由弧度制的定义可得：，解得：，‎ 则扇形的面积：.‎ ‎【点睛】‎ 本题主要考查弧度制的定义与应用，扇形面积公式的应用等知识，意在考查学生的转化能力和计算求解能力.‎ ‎15．在200个产品中，有一等品40个、二等品60个、三等品100个，用分层抽样的方法抽取一个容量为40的样本，则从二等品中应抽取_____个.‎ ‎【答案】‎ ‎【解析】试题分析：由题意得，抽样比例为，故从二等品中应抽取．‎ ‎【考点】分层抽样.‎ 三、解答题 ‎16．已知两圆和相切，求实数的值。‎ ‎【答案】或0‎ ‎【解析】分类讨论两圆外切和内切两种情况即可确定实数a的值.‎ ‎【详解】‎ 题中所给两圆的圆心坐标分别为：，半径分别为：，‎ 若两圆外切，则：，解得：，‎ 若两圆内切，则：，解得：，‎ 综上可得，a的值为或0.‎ ‎【点睛】‎ 判断两圆的位置关系常用几何法，即用两圆圆心距与两圆半径和与差之间的关系，一般不采用代数法．两圆相切注意讨论内切外切两种情况.‎ ‎17．求过原点且倾斜角为的直线被圆截得的弦长。‎ ‎【答案】‎ ‎【解析】首先求得圆心到直线的距离，然后利用弦长公式可得弦长.‎ ‎【详解】‎ 过原点且倾斜角为的直线方程为，‎ 圆的标准方程为，圆心坐标为，半径为 圆心到直线的距离：，‎ 结合弦长公式可得弦长为：.‎ ‎【点睛】‎ 本题主要考查点到直线距离公式，圆的弦长公式等知识，意在考查学生的转化能力和计算求解能力.‎ ‎18．求经过两直线与的交点M,且与直线平行的直线的方程，并求与之间的距离.‎ ‎【答案】直线方程： ，距离为：‎ ‎【解析】由方程组 ，可得交点M．又所求直线与直线2x+y+5＝0平行，可得k＝﹣2．再利用点斜式即可得出．利用两条平行线间的距离公式求出l1与l2‎ 间的距离即可．‎ ‎【详解】‎ 由方程组，解得x＝﹣1，y＝2．所以交点M（﹣1，2）．又因为所求直线与直线2x+y+5＝0平行，所以k＝﹣2．‎ 由点斜式得所求直线方程为y﹣2＝﹣2（x+1）．即2x+y＝0．l1与l2间的距离d＝ ．‎ ‎【点睛】‎ 本题考查了相互平行的直线斜率之间的关系、点斜式方程，考查两条平行线间的距离公式，属于基础题．‎ ‎19．已知圆与圆相交于A，B两点.‎ ‎（1）求公共线AB所在的直线的方程；‎ ‎（2）求圆心在直线上，且经过A,B两点的圆的方程。‎ ‎【答案】(1)x－2y＋4＝0.(2)⊙M：(x＋3)2＋(y－3)2＝10.‎ ‎【解析】试题分析：（1）由两圆方程相减即得公共弦AB所在的直线方程；（2）求出过的直线与直线y=-x的交点，可得圆心坐标，求出圆心到AB的距离，可得半径，从而可得圆的方程 试题解析：（1）⇒x－2y＋4＝0．‎ ‎（2）由（1）得x＝2y－4，代入x2＋y2＋2x＋2y－8＝0中得：y2－2y＝0．‎ ‎∴或，即A（－4，0），B（0，2），‎ 又圆心在直线y＝－x上，设圆心为M（x，－x），‎ 则|MA|＝|MB|，解得M（－3，3），‎ ‎∴⊙M：（x＋3）2＋（y－3）2＝10．‎ ‎【考点】直线与圆相交的性质 ‎20．某种产品的宣传费（单位：万元）与销售额（单位：万元）之间有如下对应数据：‎ ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ ‎30‎ ‎40‎ ‎60‎ ‎50‎ ‎70‎ ‎（1）求线性回归方程.‎ ‎（2）试预测宣传费为10万元时，销售额为多少？‎ 参考数值：，‎ ‎【答案】（1）（2）82.5万元 ‎【解析】(1)由题意结合线性回归方程的计算公式可得其线性回归方程；‎ ‎(2)利用回归方程的预测作用即可求得其销售额.‎ ‎【详解】‎ ‎（1）计算得，，又，，‎ 得，‎ 则,所以回归方程为.‎ ‎（2）由（1）知，所以当时，，‎ 故销售额为82.5万元.‎ ‎【点睛】‎ 一是回归分析是对具有相关关系的两个变量进行统计分析的方法，只有在散点图大致呈线性时，求出的线性回归方程才有实际意义，否则，求出的线性回归方程毫无意义．二是根据回归方程进行预报，仅是一个预报值，而不是真实发生的值．‎ ‎21．某地统计局调查了10000名居民的月收入，并根据所得数据绘制了样本的频率分布直方图如图所示。‎ ‎（1）求居民月收入在[3000,3500）内的频率；‎ ‎（2）根据频率分布直方图求出样本数据的中位数；‎ ‎（3）为了分析居民的月收入与年龄、职业等方面的关系，必须按月收入再从这10000中用分层抽样的方法抽出100人做进一步分析，则应从月收入在[2500,3000)内的居民中抽取多少人？‎ ‎【答案】（1）0.15（2）2400（3）25人 ‎【解析】(1)由频率分布直方图计算可得月收入在[3000,3500）内的频率；‎ ‎(2)分别计算小长方形的面积值，利用中位数的特点即可确定中位数的值；‎ ‎(3)首先确定10000人中月收入在[2500,3000]内的人数，然后结合分层抽样的特点可得应抽取的人数.‎ ‎【详解】‎ ‎（1）居民月收入在[3000,3500]内的频率为 ‎（2）因为，‎ ‎，‎ ‎，‎ ‎，‎ 所以样本数据的中位数为.‎ ‎（3）居民月收入在[2500,3000]内的频率为，‎ 所以这10000人中月收入在[2500,3000]内的人数为.‎ 从这10000人中用分层抽样的方法抽出100人，‎ 则应从月收入在[2500,3000]内的居民中抽取(人).‎ ‎【点睛】‎ 利用频率分布直方图求众数、中位数和平均数时，应注意三点：①最高的小长方形底边中点的横坐标即是众数；②中位数左边和右边的小长方形的面积和是相等的；③平均数是频率分布直方图的“重心”，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.‎