【数学】2021届一轮复习北师大版(文)第二章 第6讲 对数函数学案
第6讲 对数函数
一、知识梳理
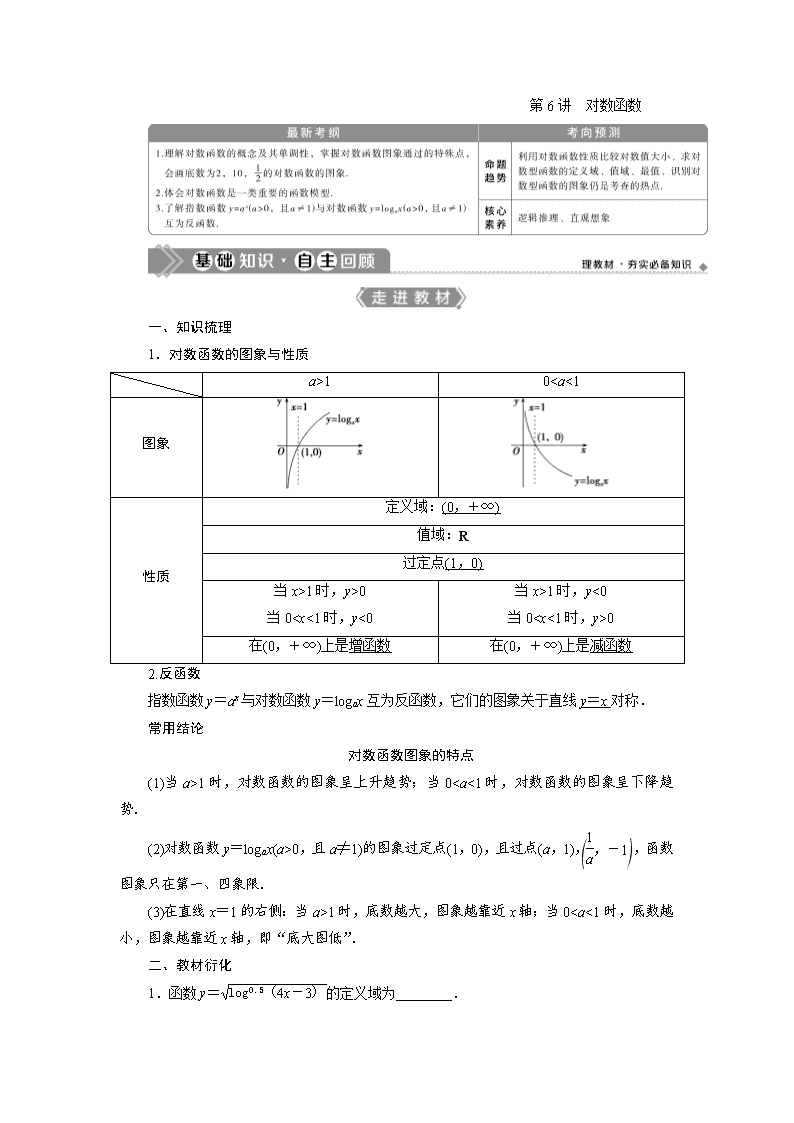
1.对数函数的图象与性质
a>1
0
1时,y>0
当01时,y<0
当00
在(0,+∞)上是增函数
在(0,+∞)上是减函数
2.反函数
指数函数y=ax与对数函数y=logax互为反函数,它们的图象关于直线y=x对称.
常用结论
对数函数图象的特点
(1)当a>1时,对数函数的图象呈上升趋势;当00,且a≠1)的图象过定点(1,0),且过点(a,1),,函数图象只在第一、四象限.
(3)在直线x=1的右侧:当a>1时,底数越大,图象越靠近x轴;当0a>b
一、思考辨析
判断正误(正确的打“√”,错误的打“×”)
(1)函数y=log2x及y=log3x都是对数函数.( )
(2)对数函数y=logax(a>0且a≠1)在(0,+∞)上是增函数.( )
(3)函数y=ln 与y=ln(1+x)-ln(1-x)的定义域相同.( )
(4)对数函数y=logax(a>0且a≠1)的图象过定点(1,0),且过点(a,1),函数图象只经过第一、四象限.( )
答案:(1)× (2)× (3)× (4)√
二、易错纠偏
(1)忽略真数大于零致误;
(2)忽视对底数的讨论致误.
1.函数f(x)=log2x2的递增区间为 .
解析:设t=x2,因为y=log2t在定义域上是增函数,所以求原函数的递增区间,即求函数t=x2的递增区间,所以所求区间为(0,+∞).
答案:(0,+∞)
2.函数y=logax(a>0,a≠1)在[2,4]上的最大值与最小值的差是1,则a= .
解析:分两种情况讨论:①当a>1时,有loga4-loga2=1,解得a=2;②当00,且a≠1)的值域为{y|y≥1},则函数y=loga|x|
的图象大致是( )
(2)若方程4x=logax在上有解,则实数a的取值范围为 .
【解析】 (1)由于y=a|x|的值域为{y|y≥1},所以a>1,则y=loga|x|在(0,+∞)上是增函数,又函数y=loga|x|的图象关于y轴对称.因此y=loga|x|的图象应大致为选项B.
(2)构造函数f(x)=4x和g(x)=logax,
当a>1时不满足条件,
当01时不满足条件,当0,所以a的取值范围为.
答案:
对于较复杂的不等式恒成立问题,可借助函数图象解决,具体做法为:
(1)对不等式变形,使不等号两边分别对应两函数f(x),g(x);
(2)在同一直角坐标系下作出两个函数f(x)与g(x)的图象;
(3)比较当x在某一范围内取值时图象的上下位置来确定参数的取值.
1.函数y=2log4(1-x)的图象大致是( )
解析:选C.函数y=2log4(1-x)的定义域为(-∞,1),排除A,B;函数y=2log4(1-x)在定义域上单调递减,排除D.选C.
2.已知函数f(x)=且关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是 .
解析:如图,在同一直角坐标系中分别作出y=f(x)与y=-x+a的图象,其中a表示直线在y轴上的截距.
由图可知,当a>1时,直线y=-x+a与y=log2x只有一个交点.
答案:(1,+∞)
对数函数的性质及应用(多维探究)
角度一 比较对数值的大小
(2019·高考天津卷)已知a=log27,b=log38,c=0.30.2,则a,b,c的大小关系为( )
A.clog24=2,b=log381,c=0.30.2<0.30=1,所以c0且a≠1)满足f0的解集为( )
A.(0,1) B.(-∞,1)
C.(1,+∞) D.(0,+∞)
【解析】 法一:因为函数f(x)=logax(a>0且a≠1)在(0,+∞)上为单调函数,而<且f0⇒2x-1>1,所以x>1.
法二:由floga,
所以loga2-11,由f(2x-1)>0得loga(2x-1)>0,所以2x-1>1,即x>1.
【答案】 C
解对数不等式的函数及方法
(1)形如logax>logab的不等式,借助y=logax的单调性求解,如果a的取值不确定,需分a>1与0b的不等式,需先将b化为以a为底的对数式的形式.
角度三 对数型函数的综合问题
已知函数f(x)=log4(ax2+2x+3).
(1)若f(1)=1,求f(x)的单调区间;
(2)若f(x)的最小值为0,求a的值.
【解】 (1)因为f(1)=1,所以log4(a+5)=1,因此a+5=4,即a=-1,
所以f(x)=log4(-x2+2x+3).
由-x2+2x+3>0得-120=1,c=0.20.3<0.20=1且c>0,所以a1时,1-log2x≤2,解得x≥,所以x>1.综上可知x≥0.
思想方法系列4 分类讨论思想研究指数、对数函数的性质
已知函数f(x)=loga(2x-a)(a>0且a≠1)在区间[,]上恒有f(x)>0,则实数a的取值范围是( )
A.(,1) B.[,1)
C.(,1) D.[,1)
【解析】 当00,即0<-a<1,解得1时,函数f(x)在区间[,]上是增函数,所以loga(1-a)>0,即1-a>1,解得a<0,此时无解.综上所述,实数a的取值范围是(,1).
【答案】 A
本题利用了分类讨论思想,在研究指数、对数函数的性质时,常对底数a的值进行分类讨论,实质上分类讨论就是“化整为零,各个击破,再集零为整”的数学思想.
已知函数y=a2x+2ax-1(a>0,且a≠1),当x≥0时,求函数的值域.
解:y=a2x+2ax-1,令t=ax,
则y=g(t)=t2+2t-1=(t+1)2-2.
当a>1时,因为x≥0,所以t≥1,所以当a>1时,y≥2.
当01时,函数的值域是[2,+∞);
当00且a≠1)的反函数,且f(2)=1,则f(x)=( )
A.log2x B.
C.logx D.2x-2
解析:选A.由题意知f(x)=logax(a>0且a≠1),因为f(2)=1,所以loga2=1,所以a=2.所以f(x)=log2x.故选A.
3.(2020·东北三省四市一模)若a=log2,b=0.48,c=ln 2,则a,b,c的大小关系是( )
A.a0,所以0ln=,即c>,所以af(2) B.f(a+1)f(2).
5.(2020·河南平顶山模拟)函数f(x)=loga|x+1|(a>0,a≠1),当x∈(-1,0)时,恒有f(x)>0,则( )
A.f(x)在(-∞,0)上是减函数
B.f(x)在(-∞,-1)上是减函数
C.f(x)在(0,+∞)上是增函数
D.f(x)在(-∞,-1)上是增函数
解析:选D.由题意,函数f(x)=loga|x+1|(a>0且a≠1),则说明函数f(x)关于直线x=-1对称,当x∈(-1,0)时,恒有f(x)>0,即|x+1|∈(0,1),f(x)>0,则00,a≠1)的图象过定点A,若点A也在函数f(x)=2x+b的图象上,则f(log23)= .
解析:由题意得A(2,0),因此f(2)=4+b=0,b=-4,从而f(log23)=3-4=-1.
答案:-1
7.若函数f(x)=logax(00,且a≠1,
所以u=ax-3为增函数,
所以若函数f(x)为增函数,则f(x)=logau必为增函数,
所以a>1.
又u=ax-3在[1,3]上恒为正,
所以a-3>0,即a>3.
答案:(3,+∞)
9.已知函数f(x-3)=loga(a>0,a≠1).
(1)求f(x)的解析式;
(2)判断f(x)的奇偶性,并说明理由.
解:(1)令x-3=u,则x=u+3,于是f(u)=loga(a>0,a≠1,-30,a≠1,-30且a≠1),且f(1)=2.
(1)求实数a的值及f(x)的定义域;
(2)求f(x)在区间上的最大值.
解:(1)因为f(1)=2,所以loga4=2(a>0,a≠1),所以a=2.
由得-10,a>0.
(1)求函数f(x)的定义域;
(2)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围.
解:(1)由x+-2>0,得>0.
因为x>0,所以x2-2x+a>0.
当a>1时,定义域为(0,+∞);
当a=1时,定义域为(0,1)∪(1,+∞);
当00,
即x+-2>1对x∈[2,+∞)恒成立,
即a>-x2+3x对x∈[2,+∞)恒成立,
记h(x)=-x2+3x,x∈[2,+∞),则只需a>h(x)max.
而h(x)=-x2+3x=-
+在[2,+∞)上是减函数,所以h(x)max=h(2)=2,故a>2.