【数学】2019届一轮复习苏教版 复数、算法 学案

【数学】2019届一轮复习苏教版 复数、算法 学案

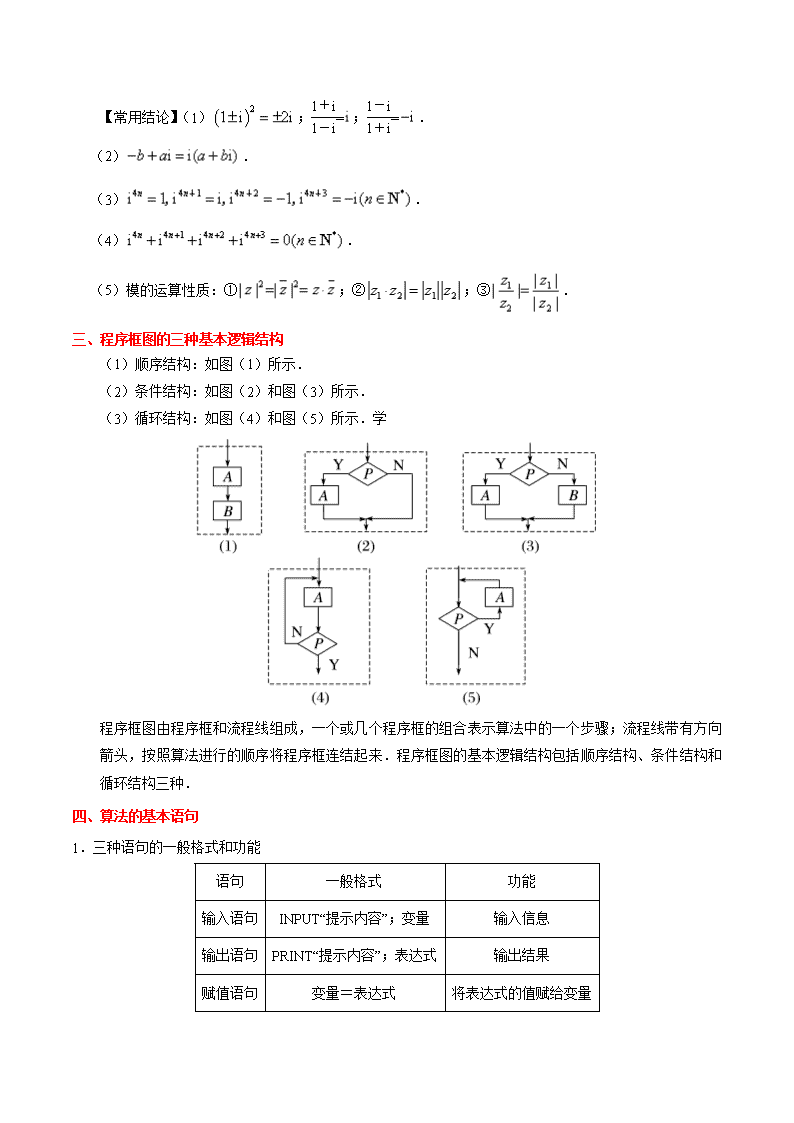
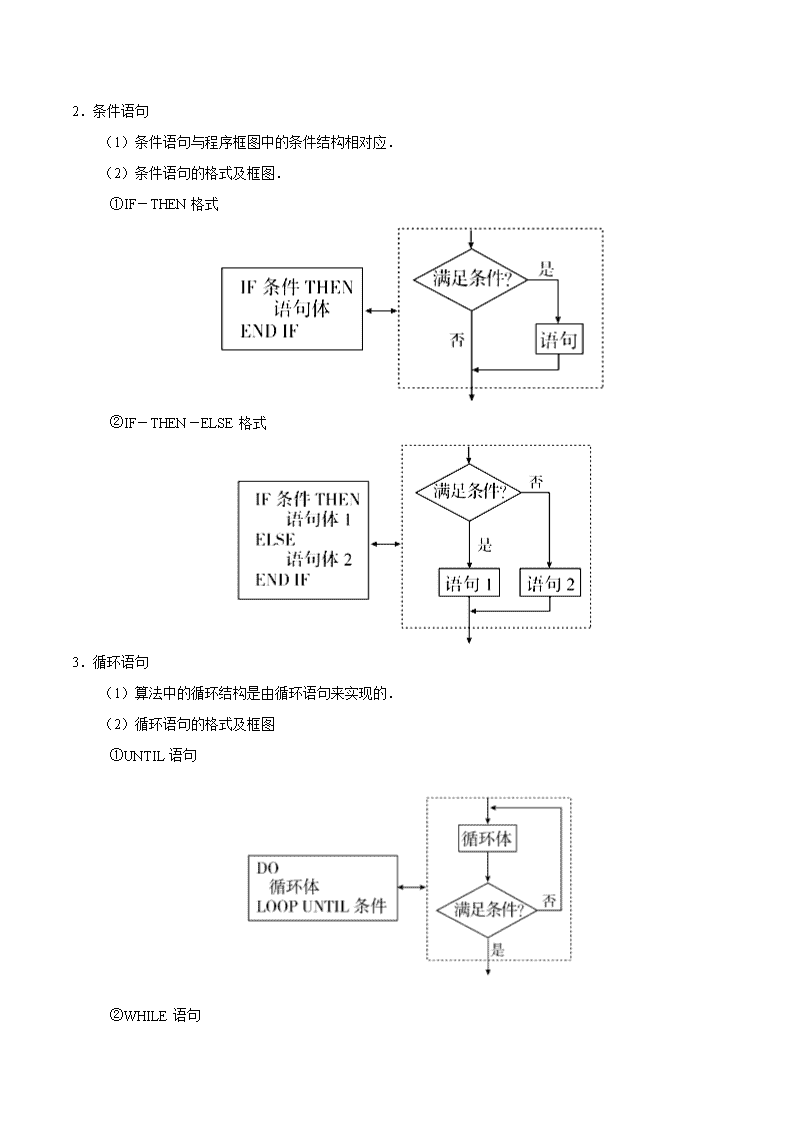
专题02 复数、算法 一、复数的概念 二、复数的加、减、乘、除运算法则 设，则 ‎①加法：；‎ ‎②减法：；‎ ‎③乘法：；‎ ‎④除法：．‎ ‎【常用结论】（1）；=；=．‎ ‎（2）．‎ ‎（3）．‎ ‎（4）．‎ ‎（5）模的运算性质：①；②；③．‎ 三、程序框图的三种基本逻辑结构 ‎（1）顺序结构：如图（1）所示．‎ ‎（2）条件结构：如图（2）和图（3）所示．‎ ‎（3）循环结构：如图（4）和图（5）所示．学 ‎ 程序框图由程序框和流程线组成，一个或几个程序框的组合表示算法中的一个步骤；流程线带有方向箭头，按照算法进行的顺序将程序框连结起来．程序框图的基本逻辑结构包括顺序结构、条件结构和循环结构三种．‎ 四、算法的基本语句 ‎1．三种语句的一般格式和功能 语句 一般格式 功能 输入语句 INPUT“提示内容”；变量 输入信息 输出语句 PRINT“提示内容”；表达式 输出结果 赋值语句 变量＝表达式 将表达式的值赋给变量 ‎2．条件语句 ‎（1）条件语句与程序框图中的条件结构相对应．‎ ‎（2）条件语句的格式及框图．‎ ‎①IF－THEN格式 ‎②IF－THEN－ELSE格式 ‎3．循环语句 ‎（1）算法中的循环结构是由循环语句来实现的．‎ ‎（2）循环语句的格式及框图 ‎①UNTIL语句 ‎②WHILE语句 ‎1．i为虚数单位，i607的共轭复数为________________．‎ ‎2．已知i为虚数单位，则复数=________________．‎ ‎3．已知，i是虚数单位．若，则a=________________．‎ ‎4．设复数 满足=i，则| |=________________．学 ‎ ‎5．若为虚数单位，，则________________．‎ ‎6．设复数 1和 2在复平面内的对应点关于坐标原点对称，且 1=3−2i，则 1· 2=________________．‎ ‎7．已知复数，则复数的共轭复数为________________．‎ ‎8．若复数在复平面内对应的点在第二象限，则实数a的取值范围是________________．‎ ‎9．若复数(为虚数单位)为实数，则实数等于________________．‎ ‎10．复平面内，复数对应的点位于第________________象限．‎ ‎11．设，其中x，y是实数，则________________．‎ ‎12．已知复数的实部与虚部的和为，则实数的值为________________．‎ ‎13．若复数在复平面内的对应点关于实轴对称，，则________________．‎ ‎14．已知复数，是虚数单位，在复平面上对应的点在第四象限，则实数的取值范围是________________．‎ ‎15．某程序框图如图所示，若该程序运行后输出的值是，则a＝________________．‎ ‎　‎ ‎16．根据如图所示的框图，对大于2的整数N，输出的数列的通项公式是an＝________________．‎ ‎17．如图是一个算法流程图，若输入的值为，则输出的值是________________．‎ ‎18．阅读下面的程序框图，运行相应的程序，若输入的值为24，则输出的值为________________．‎ ‎19．下述程序的功能是________________．学 ‎ ‎20．执行如图所示的程序，若输出y的值为2，则输入x的值为________________．‎ ‎（1）复数的运算与复数几何意义的综合题．先利用复数的运算法则化简，一般化为a＋bi(a，b∈R)的形式，再结合复数的几何意义解答．复数的除法运算主要是利用分子、分母同乘以分母的共轭复数进行运算化简．‎ ‎（2）复数的综合运算．分别运用复数的乘法、除法法则进行运算，要注意运算顺序，要先算乘除，后算加减，有括号要先算括号里面的．‎ ‎（3）注意区分处理框与输入框，处理框主要是赋值、计算，而输入框只是表示一个算法输入的信息．‎ ‎（4）循环结构中必有条件结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．注意区分当型循环与直到型循环．直到型循环是“先循环，后判断，条件满足时终止循环”；而当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反．‎ ‎（5）关于赋值语句，有以下几点需要注意：‎ ‎①赋值号左边只能是变量名字，而不是表达式，例如3＝m是错误的．‎ ‎②赋值号左右不能对换，赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量，例如Y＝x，表示用x的值替代变量Y的原先的取值，不能改写为x＝Y．因为后者表示用Y的值替代变量x的值．‎ ‎③在一个赋值语句中只能给一个变量赋值，不能出现多个“＝”．‎ ‎（6）顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．‎ ‎（7）利用条件结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足．‎ ‎（8）对于循环结构，‎ ‎①已知程序框图，求输出的结果．注意按程序框图的流程依次执行，最后得出结果．‎ ‎②完善程序框图问题时，注意结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．‎ ‎③对于辨析程序框图功能问题，可将程序执行几次，即可根据结果作出判断．‎ ‎1．已知为虚数单位，复数，则复数的实部是________________．‎ ‎2．设，为虚数单位，且，则________________．‎ ‎3．若复数是虚数单位)，且为纯虚数，则实数=________________．‎ ‎4．设为实数，若复数，则________________，________________．‎ ‎5．已知复数，则复数的虚部为________________．‎ ‎6．中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的依次输入的a为2，2，5，则输出的s=________________．‎ ‎7．执行下面的程序框图，如果输入的，则输出x，y的值满足________________．‎ ‎8．执行如图所示的程序框图，输出的值为________________．‎ ‎9．执行下面的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为________________．‎ ‎10．如果复数在复平面内对应的点位于第四象限，那么角在第________________象限．‎ ‎11．设i是虚数单位，是复数 的共轭复数．若 ·i＋2=2 ，则 =________________．‎ ‎12．设复数a＋bi(a，b∈R)的模为，则(a＋bi)(a−bi)=________________．‎ ‎13．执行下面的程序框图，如果输入的，则输出的________________．‎ ‎1．【答案】i ‎【解析】∵，∴i607的共轭复数为i．‎ ‎2．【答案】1−i ‎【解析】．‎ ‎3．【答案】1或−1‎ ‎【解析】由得，所以．‎ ‎【名师点睛】复数的共轭复数是，据此结合已知条件，求得的值．‎ ‎4．【答案】1‎ ‎【解析】由题意知，所以，所以| |=1．‎ ‎5．【答案】2‎ ‎【解析】，．‎ ‎6．【答案】−5＋12i ‎【解析】 1=3−2i，由题意知 2=−3＋2i，∴ 1· 2=(3−2i)·(−3＋2i)=−5＋12i．‎ ‎7．【答案】‎ ‎【解析】因为，所以，所以．‎ ‎【名师点睛】复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题，只需把复数化为代数形式，列出实部和虚部满足的方程(不等式)组即可．复数 =a＋bi复平面内的点 (a，b)(a，b∈R)．复数 =a＋bi(a，b∈R)平面向量．‎ ‎9．【答案】‎ ‎【解析】由为实数得．‎ ‎10．【答案】二 ‎【解析】由题设可知，故依据复数的实部与虚部的符号可知该复数对应的点位于第二象限．‎ ‎11．【答案】‎ ‎【解析】因为所以．‎ ‎12．【答案】‎ ‎【解析】∵，∴，解得．‎ ‎13．【答案】‎ ‎【解析】∵复数 1， 2在复平面内的对应点关于实轴对称，，∴，‎ 则．‎ ‎14．【答案】‎ ‎【解析】因为，所以由题意得，故应填．‎ ‎17．【答案】‎ ‎【解析】由题意得，故答案为．‎ ‎【名师点睛】算法与流程图的考查，侧重于对流程图循环结构、条件结构和伪代码的考查．先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环的初始条件、循环次数、循环的终止条件，要通过循环规律，明确流程图研究的数学问题，是求和还是求项．‎ ‎18．【答案】2‎ ‎【解析】初始：，进入循环后的值依次为，输出．‎ ‎【名师点睛】识别算法框图和完善算法框图是近几年高考的重点和热点．对于此类问题：‎ ‎①要明确算法框图中的顺序结构、条件结构和循环结构；‎ ‎②要识别运行算法框图，理解框图解决的问题；‎ ‎③按照框图的要求一步一步进行循环，直到跳出循环体输出结果． ‎ ‎19．【答案】求满足的最小正整数 ‎【解析】由题意得，程序的作用是求满足的最小正整数的值．‎ ‎20．【答案】‎ ‎【解析】当时，由条件知，解得，符合题意；‎ 当时，由条件知，此方程无解．故．故答案为．‎ ‎1．【答案】−1‎ ‎【解析】由题意可得：，则复数的实部是−1．‎ ‎4．【答案】‎ ‎【解析】由得，则，解得．‎ ‎5．【答案】‎ ‎【解析】因为，所以复数的虚部为．‎ ‎6．【答案】17‎ ‎【解析】由题意，，输入，则，循环；输入，则，循环；输入，，结束循环．故输出的．‎ ‎7．【答案】‎ ‎【解析】当时，，不满足；‎ ‎，不满足；，满足；输出，则输出的的值满足．‎ ‎8．【答案】‎ ‎【名师点睛】解决此类型问题时要注意：‎ 第一，要明确是当型循环结构，还是直到型循环结构，并根据各自的特点执行循环体；‎ 第二，要明确图中的累计变量，明确每一次执行循环体前和执行循环体后，变量的值发生的变化；‎ 第三，要明确循环体终止的条件是什么，会判断什么时候终止循环体，争取写出每一个循环，这样避免出错．‎ ‎9．【答案】2‎ ‎【解析】阅读程序框图，程序运行如下：‎ 首先初始化数值：，然后进入循环体：‎ 此时应满足，执行循环语句：；‎ 此时应满足，执行循环语句：；‎ 此时满足，可以跳出循环，则输入的正整数N的最小值为2．‎ ‎10．【答案】二 ‎【解析】∵复数在复平面内对应的点位于第四象限，∴，∴角所在的象限是第二象限．‎ ‎11．【答案】1＋i ‎【解析】设 =a＋bi(a，b∈R)，则 ·i＋2=(a＋bi)·(a−bi)·i＋2=2＋(a2＋b2)i，故2=2a，a2＋b2=2b，解得a=1，b=1，即 =1＋i．‎ ‎12．【答案】3‎ ‎【解析】复数a＋bi(a，b∈R)的模为=，则a2＋b2=3，则(a＋bi)(a−bi)=a2−(bi)2=a2−b2·i2=a2＋b2=3．‎ ‎13．【答案】3‎ 个人总结 ‎________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________‎