【数学】2018届一轮复习北师大版第二章函数导数及其应用第八节函数与方程教案

【数学】2018届一轮复习北师大版第二章函数导数及其应用第八节函数与方程教案

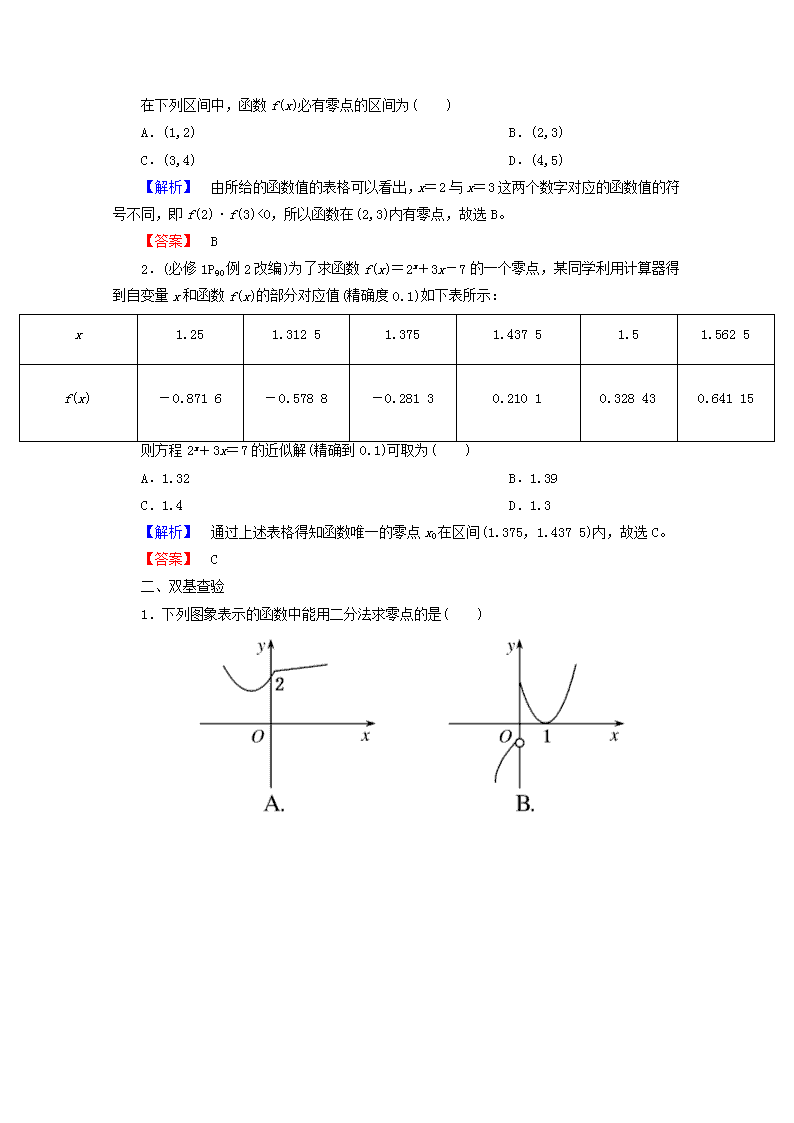
第八节　函数与方程 ‎☆☆☆2017考纲考题考情☆☆☆‎ 考纲要求 真题举例 命题角度 ‎1.结合二次函数的图象，了解函数的零点与方程根的联系，判断一元二次方程根的存在性及根的个数；‎ ‎2.根据具体函数的图象，能够用二分法求相应方程的近似解。‎ ‎2016，全国卷Ⅰ，21,12分(导数与函数的零点)‎ ‎2016，天津卷，8,5分(函数单调性与函数的零点)‎ ‎2014，全国卷Ⅰ，11,5分(函数的零点，参数的取值范围)‎ ‎1.函数零点个数、存在区间及方程解的确定与应用是高考内容之一；‎ ‎2.常与函数的图象与性质交汇命题，主要考查函数与方程、转化与化归、数形结合思想。‎ 微知识　小题练 自|主|排|查 ‎1．函数的零点 ‎(1)函数零点的定义 对于函数y＝f(x)(x∈D)，把使f(x)＝0的实数x叫做函数y＝f(x)(x∈D)的零点。‎ ‎(2)几个等价关系 方程f(x)＝0有实数根⇔函数y＝f(x)的图象与x轴有交点⇔函数y＝f(x)有零点。‎ ‎(3)函数零点的判定(零点存在性定理)‎ 如果函数y＝f(x)在区间[a，b]上的图象是连续不断的一条曲线，并且有f(a)·f(b)<0，那么，函数y＝f(x)在区间(a，b)内有零点，即存在c∈(a，b)，使得f(c)＝0，这个c也就是方程f(x)＝0的根。‎ ‎2．二分法 对于在区间[a，b]上连续不断且f(a)·f(b)<0的函数y＝f(x)，通过不断地把函数f(x)的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法。‎ ‎3．二次函数y＝ax2＋bx＋c(a>0)的图象与零点的关系 Δ>0‎ Δ＝0‎ Δ<0‎ 二次函数 y＝ax2＋bx＋c ‎(a>0)的图象 与x轴的交点 ‎(x1,0)，(x2,0)‎ ‎(x1,0)‎ 无交点 零点个数 ‎2‎ ‎1‎ ‎0‎ 微点提醒 ‎1．有关函数零点的结论 ‎(1)若连续不断的函数f(x)在定义域上是单调函数，则f(x)至多有一个零点。‎ ‎(2)连续不断的函数，其相邻两个零点之间的所有函数值保持同号。‎ ‎(3)连续不断的函数图象通过零点时，函数值可能变号，也可能不变号。‎ ‎2．三个等价关系 方程f(x)＝0有实数根⇔函数y＝f(x)的图象与x轴有交点⇔函数y＝f(x)有零点。‎ 小|题|快|练 一 、走进教材 ‎1．(必修1P‎92A组T2改编)已知函数f(x)的图象是连续不断的，且有如下对应值表：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ f(x)‎ ‎－4‎ ‎－2‎ ‎1‎ ‎4‎ ‎7‎ 在下列区间中，函数f(x)必有零点的区间为(　　)‎ A．(1,2) B．(2,3)‎ C．(3,4) D．(4,5)‎ ‎【解析】　由所给的函数值的表格可以看出，x＝2与x＝3这两个数字对应的函数值的符号不同，即f(2)·f(3)<0，所以函数在(2,3)内有零点，故选B。‎ ‎【答案】　B ‎2．(必修1P90例2改编)为了求函数f(x)＝2x＋3x－7的一个零点，某同学利用计算器得到自变量x和函数f(x)的部分对应值(精确度0.1)如下表所示：‎ x ‎1.25‎ ‎1.312 5‎ ‎1.375‎ ‎1.437 5‎ ‎1.5‎ ‎1.562 5‎ f(x)‎ ‎－0.871 6‎ ‎－0.578 8‎ ‎－0.281 3‎ ‎0.210 1‎ ‎0.328 43‎ ‎0.641 15‎ 则方程2x＋3x＝7的近似解(精确到0.1)可取为(　　)‎ A．1.32 B．1.39‎ C．1.4 D．1.3‎ ‎【解析】　通过上述表格得知函数唯一的零点x0在区间(1.375，1.437 5)内，故选C。‎ ‎【答案】　C 二、双基查验 ‎1．下列图象表示的函数中能用二分法求零点的是(　　)‎ ‎【解析】　A中函数没有零点，因此不能用二分法求零点；B中函数的图象不连续；D中函数在x轴下方没有图象。故选C。‎ ‎【答案】　C ‎2．已知函数f(x)＝－log2x，在下列区间中，包含f(x)零点的区间是(　　)‎ A．(0,1) B．(1,2)‎ C．(2,4) D．(4，＋∞)‎ ‎【解析】　因为f(1)＝6－log21＝6>0，f(2)＝3－log22＝2>0，f(4)＝－log24＝－<0，所以函数f(x)的零点所在区间为(2,4)，故选C。‎ ‎【答案】　C ‎3．函数f(x)＝ex＋3x的零点个数是(　　)‎ A．0 B．1‎ C．2 D．3‎ ‎【解析】　由已知得f′(x)＝ex＋3>0，‎ 所以f(x)在R上单调递增，‎ 又f(－1)＝e－1－3<0，‎ f(1)＝e＋3>0，‎ 因此f(x)的零点个数是1。故选B。‎ ‎【答案】　B ‎4．函数f(x)＝kx＋1在[1,2]上有零点，则k的取值范围是________。‎ ‎【答案】　 ‎5．函数y＝(k－8)x2＋x＋1至多有一个零点，则k的取值范围为________。‎ ‎【解析】　①k＝8时符合；‎ ‎②k≠8时对应方程Δ＝1－4(k－8)≤0，‎ 解得k≥，‎ 所以k≥或k＝8。‎ ‎【答案】　∪{8}‎ 微考点　大课堂 考点一 ‎ 判断函数零点所在区间 ‎【典例1】　函数f(x)＝log3x＋x－2的零点所在的区间为(　　)‎ A．(0,1)　　　　　　 B．(1,2)‎ C．(2,3) D．(3,4)‎ ‎【解析】　函数f(x)＝log3x＋x－2的定义域为(0，＋∞)，并且f(x)在(0，＋∞)上单调递增，图象是一条连续曲线。‎ 又f(1)＝－1<0，f(2)＝log32>0，f(3)＝2>0，根据零点存在性定理，可知函数f(x)＝log3x＋x－2有唯一零点，且零点在区间(1,2)内。故选B。‎ ‎【答案】　B 反思归纳　函数的零点存在性定理只能判断函数在某个区间上的变号零点，不能判断不变号零点，而且连续函数在一个区间的端点处函数值异号是这个函数在这个区间上存在零点的充分条件，不是必要条件，所以在判断一个函数在某个区间上不存在零点时，不能完全依赖函数的零点存在性定理，要综合函数性质进行分析判断。‎ ‎【变式训练】　(2016·长沙调研)已知函数f(x)＝lnx－x－2的零点为x0，则x0所在的区间是(　　)‎ A．(0,1) B．(1,2)‎ C．(2,3) D．(3,4)‎ ‎【解析】　∵f(x)＝lnx－x－2在(0，＋∞)是增函数，‎ 又f(1)＝ln1－－1＝ln1－2<0，‎ f(2)＝ln2－0<0，‎ f(3)＝ln3－1>0，‎ ‎`∴x0∈(2,3)，故选C。‎ ‎【答案】　C 考点二 ‎ 函数零点个数的判断……多维探究 角度一：解方程确定函数零点个数 ‎【典例2】　已知函数f(x)＝若f(0)＝－2，f(－1)＝1，则函数g(x)＝f(x)＋x的零点个数为________。‎ ‎【解析】　依题意得 由此解得b＝－4，c＝－2。由g(x)＝0得f(x)＋x＝0，‎ 该方程等价于①‎ 或②‎ 解①得x＝2，解②得x＝－1或x＝－2。‎ 因此，函数g(x)＝f(x)＋x的零点个数为3。‎ ‎【答案】　3‎ 角度二：利用函数单调性确定零点个数 ‎【典例3】　函数f(x)＝ex＋x－2的零点有________个。‎ ‎【解析】　∵f′(x)＝ex＋>0，‎ ‎∴f(x)在R上单调递增，‎ 又f(0)＝1－2<0，f(1)＝e－>0，‎ ‎∴函数在区间(0,1)上有零点且只有一个。‎ ‎【答案】　1‎ 角度三：数形结合法确定函数零点个数 ‎【典例4】　(2015·天津高考)已知函数f(x)＝函数g(x)＝3－f(2－x)，则函数y＝f(x)－g(x)的零点个数为(　　)‎ A．2 B．3‎ C．4 D．5‎ ‎【解析】　由已知条件可得g(x)＝3－f(2－x)＝函数y＝f(x)－g(x)的零点个数即为函数y＝f(x)与y＝g(x)图象的交点个数，在平面直角坐标系内作出函数y＝f(x)与y＝g(x)的图象如图所示。‎ 由图可知函数y＝f(x)与y＝g(x)的图象有2个交点，所以函数y＝f(x)－g(x)的零点个数为2。故选A。‎ ‎【答案】　A 反思归纳　判断函数零点个数的3种方法 ‎1．解方程法：若对应方程f(x)＝0可解时，通过解方程，则有几个解就有几个零点。‎ ‎2．零点存在性定理法：利用定理不仅要判断函数在区间[a，b]上是连续不断的曲线，且f(a)·f(b)<0，还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点。‎ ‎3．数形结合法：转化为两个函数的图象的交点个数问题。先画出两个函数的图象，看其交点的个数，其中交点的个数，就是函数零点的个数。‎ 考点三 ‎ 函数零点的应用……多维探究 角度一：由函数零点确定参数的取值范围 ‎【典例5】　(2016·天津高考)已知函数f(x)＝(a>0，且a≠1)在R上单调递减，且关于x的方程|f(x)|＝2－x恰有两个不相等的实数解，则a的取值范围是(　　)‎ A. B. C.∪ D.∪ ‎【解析】　要使函数f(x)在R上单调递减，只需解得≤a≤，因为方程|f(x)|＝2－x恰有两个不相等的实数解，所以直线y＝2－x与函数y＝|f(x)|的图象有两个交点。如图所示。‎ 易知y＝|f(x)|的图象与x轴的交点的横坐标为－1，又≤－1≤2，故由图可知，直线y＝2－x与y＝|f(x)|的图象在x>0时有一个交点；当直线y＝2－x与y＝x2＋(‎4a－3)x＋‎3a(x<0)的图象相切时，设切点为(x0，y0)，则整理可得‎4a2－‎7a＋3＝0，解得a＝1(由于≤a≤，故a＝1舍去)或a＝。而当‎3a≤2，即a≤时，直线y＝2－‎ x与y＝|f(x)|的图象在y轴左侧有一个交点，综合可得a∈∪。故选C。‎ ‎【答案】　C 角度二：利用函数零点比较大小 ‎【典例6】　设函数f(x)＝ex＋x－2，g(x)＝lnx＋x2－3。若实数a，b满足f(a)＝0，g(b)＝0，则(　　)‎ A．g(a)＜0＜f(b) B．f(b)＜0＜g(a)‎ C．0＜g(a)＜f(b) D．f(b)＜g(a)＜0‎ ‎【解析】　∵f(x)在R上为增函数，‎ 且f(0)＝e0－2＜0，f(1)＝e－1＞0，‎ 又f(a)＝0，∴0＜a＜1。‎ ‎∵g(x)＝lnx＋x2－3，‎ ‎∴g(x)在(0，＋∞)上为增函数。‎ 又g(1)＝ln1－2＝－2＜0，g(2)＝ln2＋1＞0，且g(b)＝0，‎ ‎∴1＜b＜2，即a＜b，‎ ‎∴故选A。‎ ‎【答案】　A 反思归纳　函数零点应用问题的类型及解题策略 ‎1．已知函数零点求参数。根据函数零点或方程的根所在的区间求解参数应分三步：(1)判断函数的单调性；(2)利用零点存在性定理，得到参数所满足的不等式；(3)解不等式，即得参数的取值范围。‎ ‎2．已知函数零点的个数求参数。常利用数形结合法。‎ ‎3．借助函数零点比较大小。要比较f(a)与f(b)的大小，通常先比较f(a)、f(b)与0的大小。‎ 微考场　新提升 ‎1．函数f(x)＝xcos2x在区间[0,2π]上的零点的个数为(　　)‎ A．2 B．3‎ C．4 D．5‎ 解析　借助余弦函数的图象求解。f(x)＝xcos2x＝0⇒x＝0或cos2x＝0，又cos2x＝0在[0,2π]上有，，，，共4个根，故原函数有5个零点。故选D。‎ 答案　D ‎2．已知f(x)是定义在R上的奇函数，当x≥0时，f(x)＝x2－3x。则函数g(x)＝f(x)－x＋3的零点的集合为(　　)‎ A．{1,3} B．{－3，－1,1,3}‎ C．{2－，1,3} D．{－2－，1,3}‎ 解析　当x≥0时，函数g(x)的零点即方程f(x)＝x－3的根，由x2－3x＝x－3，解得x ‎＝1或3；‎ 当x<0时，由f(x)是奇函数，得－f(x)＝f(－x)＝x2－3(－x)，即f(x)＝－x2－3x。由f(x)＝x－3，得x＝－2－(正根舍去)。故选D。‎ 答案　D ‎3．若f(x)是奇函数，且x0是y＝f(x)＋ex的一个零点，则－x0一定是下列哪个函数的零点(　　)‎ A．y＝f(－x)ex－1 B．y＝f(x)e－x＋1‎ C．y＝exf(x)－1 D．y＝exf(x)＋1‎ 解析　由已知可得f(x0)＝－ex0，e－x‎0f(－x0)＝1，故－x0一定是y＝exf(x)－1的零点。故选C。‎ 答案　C ‎4．已知函数f(x)＝若存在实数b，使函数g(x)＝f(x)－b有两个零点，则a的取值范围是________。‎ 解析　令φ(x)＝x3(x≤a)，h(x)＝x2(x>a)，函数g(x)＝f(x)－b有两个零点，即函数y＝f(x)的图象与直线y＝b有两个交点，结合图象可得a<0或φ(a)>h(a)，即a<0或a3>a2，解得a<0或a>1，故a∈(－∞，0)∪(1，＋∞)。‎ 答案　(－∞，0)∪(1，＋∞)‎ ‎5．已知关于x的方程x2＋mx－6＝0的一个根比2大，另一个根比2小，则实数m的取值范围是________。‎ 解析　设函数f(x)＝x2＋mx－6，则根据条件有f(2)<0，即4＋‎2m－6<0，解得m<1。‎ 答案　(－∞，1)‎ 微专题　巧突破 二次函数的零点问题 ‎【典例】　m为何值时，f(x)＝x2＋2mx＋‎3m＋4。‎ ‎(1)有且仅有一个零点；‎ ‎(2)有两个零点且均比－1大。‎ ‎【解析】　(1)f(x)＝x2＋2mx＋‎3m＋4有且仅有一个零点⇔方程f(x)＝0有两个相等实根⇔Δ＝0，即‎4m2‎－4(‎3m＋4)＝0，即m2－‎3m－4＝0，∴m＝4或m＝－1。‎ ‎(2)解法一：设f(x)的两个零点分别为x1，x2，‎ 则x1＋x2＝－‎2m，x1·x2＝‎3m＋4。‎ 由题意，知⇔‎ ⇔ ‎∴－50，得a>2或a<－2。‎ 要使两根均大于1，只需小根a－>1即可，解得2

查看更多