直线的倾斜角与斜率教案4

直线的倾斜角与斜率教案4

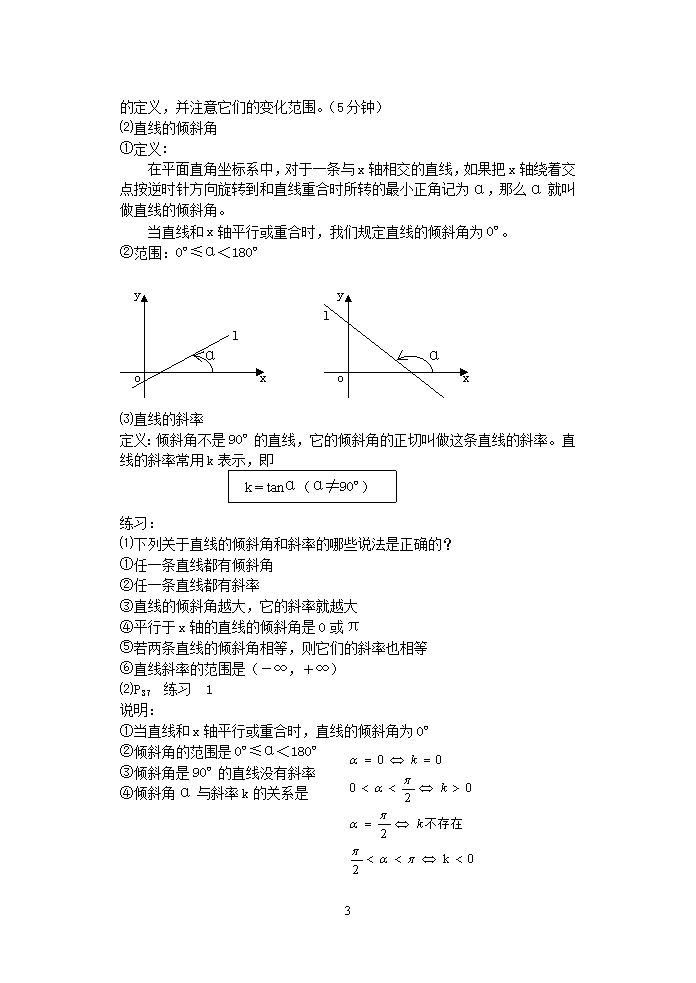
‎ ‎ 直线的倾斜角和斜率 一、素质教育目标 ‎1、知识教学点 ‎⑴“直线的方程”和“方程的直线”的概念 ‎⑵直线的倾斜角和斜率 ‎⑶斜率公式 ‎2、能力训练点 （1） 了解“直线的方程”和“方程的直线”的概念 （2） 理解直线的倾斜角和斜率的概念公式 （3） 掌握过两点的直线的斜率。‎ （4） 培养学生对数学知识的理解能力、应用能力及转化能力 二、学法指导 本节主要学习直线的方程和方程的直线间与的关系，直线的倾斜角和斜率的联系与区别，斜率的两个公式：k=tanα,k=及注意务必倾斜角不等于90º；并要会逆用公式求倾斜角。明白方向向量与斜率的关系。请沿着以下的脉络学习，学习过程中要注意概念的理解、辨析和公式的记忆以及有关思想方法的领会与把握。‎ ‎1、直线的倾斜角 ‎2、直线的斜率 ‎3、过两点的直线 ‎　的斜率公式 ‎4、直线的方向向量 直线方程 的概念 一次函数 及其图象 三、教学重点、难点　‎ ‎ 1、重点：直线的倾斜角和斜率的概念，过两点的直线的斜率公式 ‎2、难点：斜率概念的学习，过两点的直线的斜率公式 四、课时安排 本课题安排2课时 五、教与学过程设计 第一课时　直线的倾斜角和斜率 学习目标：‎ （1） 了解“直线的方程”和“方程的直线”的概念 （2） 理解直线的倾斜角和斜率的定义 （3） 已知直线的倾斜角，会求直线的斜率 （4） 已知直线的斜率，会求直线的倾斜角 9‎ ‎ ‎ 教学过程 直线和圆都是最常见的简单几何图形，在生产实践和实际生活中有广泛的应用。初中几何对直线和圆的基本性质作了比较系统的研究，初中代数研究了一次函数图象及其性质，高一数学研究了三角函数、平面向量，直线和圆的方程的内容以上述知识为基础，直线和圆的方程是解析几何的基础知识，在解决实际问题中有广泛的应用。本节要研究的是直线的两个基本概念，即直线的倾斜角和斜率。‎ ‎1、复习回顾 ‎⑴回顾一次函数的图象及性质 ‎　　形如y=kx+b(k≠0)叫做一次函数；它的图象是一条直线；当k＞0时，在R上是增函数，当k＜0时，在R上是减函数。‎ ‎⑵画出下列一次函数的图象 ‎① y = 2x + 4 ② y = －2x + 2‎ ‎ ‎ ‎ ‎ 小结：作一次函数图象的方法－由于两点确定一条直线，故可在直线上任取两点，通常取点(0 , b)与(－b/k , 0)。‎ ‎　　研究两点（－2,0）、（0,4）与函数式y = 2x + 4的关系是：这两点就是满足函数式的两对x、y的值。‎ ‎　　由作图知满足函数式y = 2x + 4的每一对x、y的值都是函数y = 2x + 4上的点；这条直线上的点的坐标都满足函数式y = 2x + 4。‎ 小结：一次函数y=kx+b(k≠0)的图象是一条直线，它是以满足y=kx+b(k≠0)的每一对x、y的值为坐标的点构成的。‎ 由于函数式y=kx+b(k≠0)也可以看成二元一次方程，所以我们说，这个方程的解和直线上的点存在这样的对应关系。‎ ‎2、讲授新课 ‎⑴直线方程的概念 以一个方程的解为坐标的点都是某条直线上的点，反过来，这条直线上的点的坐标都是这个方程的解，这时，这个方程叫做这条直线的方程，这条直线叫做这个方程的直线。‎ ‎　　在平面直角坐标系中研究直线时，就是利用直线和方程的这种关系，建立直线的方程，并通过方程来研究直线的有关问题，为此，我们先研究直线的倾斜角和斜率。正面请同学们阅读教材P34－35‎ 9‎ ‎ ‎ ‎，理解直线的倾斜角和斜率的定义，并注意它们的变化范围。（5分钟）‎ ‎⑵直线的倾斜角 ‎①定义:‎ 在平面直角坐标系中，对于一条与x轴相交的直线，如果把x轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α，那么α就叫做直线的倾斜角。‎ 当直线和x轴平行或重合时，我们规定直线的倾斜角为0º。‎ ‎②范围：0º≤α＜180º ‎　y y ‎ l ‎ l ‎　　　　　α α ‎ o x o x ‎⑶直线的斜率 定义：倾斜角不是90º的直线，它的倾斜角的正切叫做这条直线的斜率。直线的斜率常用k表示，即 k = tanα（α≠90º）‎ ‎　　　　　‎ 练习：‎ ‎⑴下列关于直线的倾斜角和斜率的哪些说法是正确的？‎ ‎①任一条直线都有倾斜角 ‎②任一条直线都有斜率 ‎③直线的倾斜角越大，它的斜率就越大 ‎④平行于x轴的直线的倾斜角是0或π ‎⑤若两条直线的倾斜角相等，则它们的斜率也相等 ‎⑥直线斜率的范围是（－∞，＋∞）‎ ‎⑵P37　练习　1‎ 说明：‎ ‎①当直线和x轴平行或重合时，直线的倾斜角为0º ‎②倾斜角的范围是0º≤α＜180º ‎③倾斜角是90º的直线没有斜率 ‎④倾斜角α与斜率k的关系是 ‎　　‎ 9‎ ‎ ‎ 练习：‎ ‎①直线l的斜率为k，倾斜角为α，若－1 kx恒成立，求k的取值范围。‎ 教学后记 9‎