平面与平面垂直的性质教案2

平面与平面垂直的性质教案2

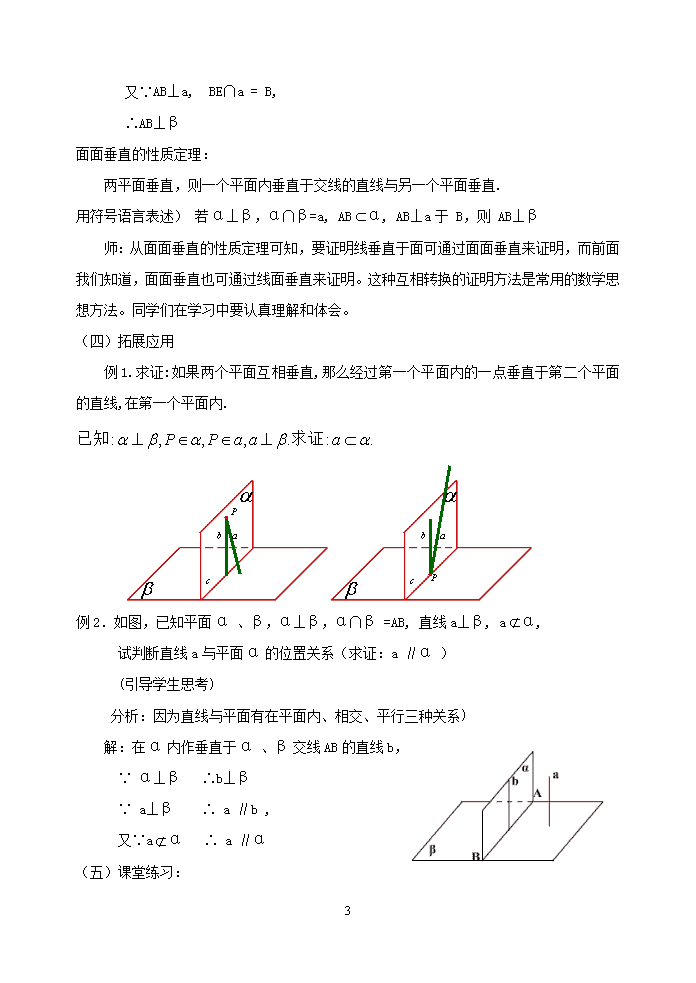
‎ ‎ ‎《2.3.4 平面与平面垂直的性质》教学设计 教学内容 人教版新教材 高二数学 第二册 第二章 第三节 第4课 教材分析 ‎ 直线与平面垂直问题是直线与平面的重要内容，也是高考考查的重点，求解的关键是根据线与面之间的互化关系，借助创设辅助线与面，找出符号语言与图形语言之间的关系把问题解决。通过对有关概念和定理的概括、证明和应用，使学生体会“转化”的观点，提高学生的空间想象力和逻辑推理能力。‎ 学情分析 ‎1.学生思维活跃，参与意识、自主探究能力较强，故采用启发、探究式教学。‎ ‎2.学生的抽象概括能力和空间想象力有待提高，故采用多媒体辅助教学。‎ 教学目标 ‎1.知识与技能 ‎（1）让学生在观察物体模型的基础上，进行操作确认，获得对性质定理的正确认识；‎ ‎（2）能运用性质定理证明一些空间位置关系的简单命题，进一步培养学生空间观念.‎ ‎（3）了解直线与平面、平面与平面垂直的判定定理和性质定理间的相互联系，掌握等价转化思想在解决问题中的运用.‎ ‎2.情感态度与价值观 ‎（1）通过“直观感知、操作确认，推理证明”， 培养学生逻辑推理能力。‎ ‎（2）发展学生的合情推理能力和空间想象力 ，培养学生的质疑思辨、创新的精神.‎ ‎（3）让学生亲身经历数学研究的过程，体验探索的乐趣，增强学习数学的兴趣.‎ 教学重、难点 重点：理解掌握面面垂直的性质定理和内容和推导。‎ 难点：运用性质定理解决实际问题。‎ 教学理念 学生是学习和发展的主体，教师是教学活动的组织者和引导者. ‎ 4‎ ‎ ‎ 设计思路：‎ 教材通过问题“如果两个平面垂直，那么一个平面内的直线是否一定垂直于另一个平面”来探索平面与平面垂直的性质定理，教学是要引导学生根据定理的自然语言，作出图形，然后用符号表示。对于平面与平面垂直的性质定理的证明，重在引导学生在平面β内找出一条与CD相交的直线垂直于AB。应用定理的关键是创设定理成立的条件。‎ 教学过程：‎ ‎(一) 复习提问 ‎1.线面垂直判定定理：‎ 如果一条直线和一个平面内两条相交直线都垂直，则这条直线垂直于这个平面.‎ ‎2.面面垂直判定定理：‎ 如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直.‎ ‎(二)引入新课 今天我们要学习“两个平面垂直的性质”，先来看下面问题：‎ 已知黑板面与地面垂直，你能在黑板面内找到一条直线与地面平行、相交或垂直吗这样的直线分别有什么性质？试说明理由！‎ ‎（三）探求新知 已知：面α⊥面β，α∩β= a, ABα, AB⊥a于 B，‎ 求证：AB⊥β ‎(让学生思考怎样证明)‎ 分析：要证明直线垂直于平面，须证明直线垂直于平面内两条相交直线，而题中条件已有一条，故可过该直线作辅助线.‎ ‎ 证明：在平面β内过B作BE⊥a，‎ 又∵AB⊥a，‎ ‎∴∠ABE为α﹣a﹣β的二面角，‎ 又∵α⊥β，‎ ‎∴∠ABE = 90° , ∴AB⊥BE ‎ 4‎ ‎ ‎ ‎ 又∵AB⊥a, BE∩a = B, ‎ ‎∴AB⊥β 面面垂直的性质定理：‎ 两平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直.‎ 用符号语言表述） 若α⊥β，α∩β=a, ABα, AB⊥a于 B，则 AB⊥β 师：从面面垂直的性质定理可知，要证明线垂直于面可通过面面垂直来证明，而前面 我们知道，面面垂直也可通过线面垂直来证明。这种互相转换的证明方法是常用的数学思想方法。同学们在学习中要认真理解和体会。‎ ‎（四）拓展应用 例1.求证:如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.‎ 例2．如图，已知平面α 、β，α⊥β，α∩β =AB, 直线a⊥β, aα,‎ 试判断直线a与平面α的位置关系（求证：a ∥α ）‎ ‎(引导学生思考)‎ 分析：因为直线与平面有在平面内、相交、平行三种关系)‎ 解：在α内作垂直于α 、β交线AB的直线b，‎ ‎∵ α⊥β ∴b⊥β ‎ ‎∵ a⊥β ∴ a ∥b , ‎ 又∵aα ∴ a ∥α ‎ ‎（五）课堂练习： ‎ 4‎ ‎ ‎ P81 练习 第1、2题 ‎ P81 A组 第1题 ‎1.如图，长方体ABCD﹣A′B′C′D′中，判断下面结论的正误。‎ ‎(1)平面ADD′A′⊥平面ABCD (2) DD′⊥ 面ABCD (3)AD′⊥ 面ABCD ‎ ‎2.空间四边形ABCD中，ΔABD与ΔBCD都为正三角形，面ABD⊥面BCD，试在平面BCD内找一点，使AE⊥面BCD,亲说明理由 解：在ΔABD中，∵AB=AD,取BD的中点E，‎ 连结AE，则AE为BD的中线 ‎∴AE⊥BD ‎ 又∵面BCD∩面ABD=BD, 面ABD⊥面BCD ‎ ‎∴AE⊥面BCD ‎（六）课堂小结： ‎ ‎1. 面面垂直判定定理：‎ 如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直.‎ ‎2. 面面垂直的性质定理：‎ 两平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直.‎ ‎② 利用性质定理解决问题 ‎（七）布置作业：‎ P81 A组 第2、5题 ‎ ‎ P82 B组 第3题 4‎