2020-2021学年高二上学期月考数学（理）试题（江西省奉新县第一中学）

2020-2021学年高二上学期月考数学（理）试题（江西省奉新县第一中学）

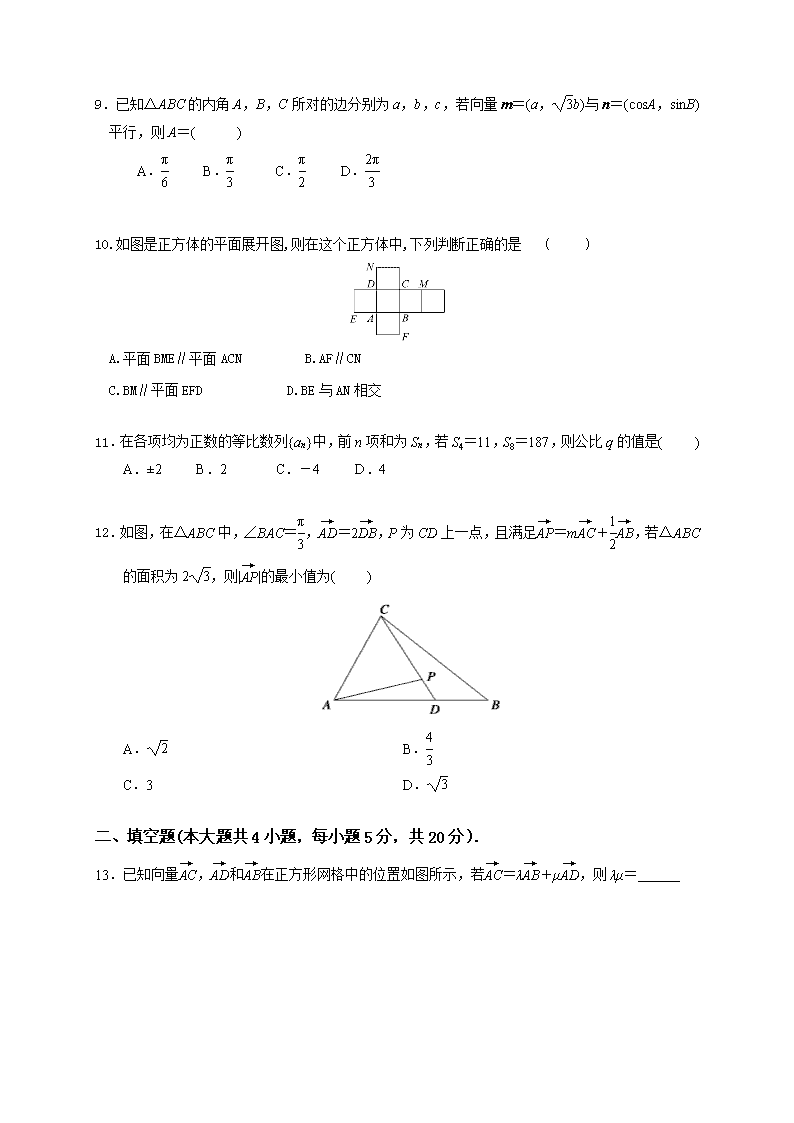
‎2022届高二上学期第一次月考数学试卷(理）‎ ‎ ‎ 一、选择题：(本大题共12小题，每小题5分，共60分。)‎ ‎1．在△ABC中，B＝45°，C＝60°，c＝1，则最短边的边长等于(　 　)‎ A. B. C. D. ‎2．下列不等式中正确的是(　 　)‎ A．a＋≥4 B．a2＋b2 ≥4ab C.≥ D．x2＋≥2 ‎3．下列各组向量中，可以作为基底的是(　 　)‎ A．e1＝(0,0)，e2＝(1，－2) B．e1＝(－1,2)，e2＝(5,7)‎ C．e1＝(3,5)，e2＝(6,10) D．e1＝(2，－3)，e2＝ ‎4．分别和两条异面直线平行的两条直线的位置关系是(　 　)‎ A．一定平行 B．一定异面 C．相交或异面 D．一定相交 ‎5．如果a>b，则下列各式正确的是(　 　)‎ A．a·lgx>b·lgx B．ax2>bx2‎ C．a2>b2 D．a·2x>b·2x ‎6.设数列{an}是公差为－2的等差数列，如果a1＋a4＋…＋a97＝50，那么a3＋a6＋a9＋…＋a99等于(　 )‎ A．－182 B．－78 C．－148 D．－82‎ ‎7．若α是第四象限角，tanα＝－，则sinα等于(　 　)‎ A． B．－ C． D．－ ‎8．设实数x，y满足约束条件则z＝3x－2y的最小值为(　 　)‎ A．－2 B．1 C．8 D．13‎ ‎9．已知△ABC的内角A，B，C所对的边分别为a，b，c，若向量m＝(a，b)与n＝(cosA，sinB ‎)平行，则A＝(　 　)‎ A． B． C． D． ‎10.如图是正方体的平面展开图,则在这个正方体中,下列判断正确的是 (　 　)‎ A.平面BME∥平面ACN B.AF∥CN C.BM∥平面EFD D.BE与AN相交 ‎11．在各项均为正数的等比数列{an}中，前n项和为Sn，若S4＝11，S8＝187，则公比q的值是(　 　)‎ A．±2 B．2 C．－4 D．4‎ ‎12．如图，在△ABC中，∠BAC＝，＝2，P为CD上一点，且满足＝m＋，若△ABC的面积为2，则||的最小值为(　 　)‎ A． B． C．3 D． 二、填空题(本大题共4小题，每小题5分，共20分）．‎ ‎13．已知向量，和在正方形网格中的位置如图所示，若＝λ＋μ，则λμ＝ ‎ ‎ ‎ ‎14．已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a＝3，C＝120°，△ABC的面积S＝，则c＝ .‎ ‎15．若关于x的不等式mx2－mx＋1<0的解集不是空集，则m的取值范围是 .‎ ‎16．函数f(x)＝()x－|sin2x|在[0，]上零点的个数为 ‎ 三：解答题(本大题共6小题，共70分．10+12+12+12+12+12=70解答时应写出必要的文字说明、证明过程或演算步骤)‎ ‎17.如图所示，A是△BCD所在平面外的一点，E，F 分别是BC，AD的中点。‎ ‎(1)判断直线EF 与平面ABC的位置关系。‎ ‎(2)判断直线EF与直线BD的位置关系。‎ ‎(3)若AC⊥BD，AC＝BD，求EF 与BD所成的角。‎ ‎18．若不等式ax2＋bx－1>0的解集是{x|10的解集．‎ ‎19．已知|a|＝4，|b|＝8，a与b的夹角是120°.‎ ‎(1)计算：①|a＋b|，②|4a－2b|；‎ ‎(2)当k为何值时，(a＋2b)⊥(ka－b)．‎ ‎20．已知函数f(x)＝sin(ωx＋φ)(ω>0,0≤φ≤π)为偶函数，且其图象上相邻的一个最高点和最低点之间的距离为.‎ ‎(1)求f(x)的解析式；‎ ‎(2)若tanα＋＝5，求的值．‎ ‎21.如图，在平面四边形ABCD中，已知AD＝AB＝1，∠BAD＝θ，且△BCD为正三角形．‎ ‎(1)将四边形ABCD的面积S表示为θ的函数；‎ ‎(2)求S的最大值及此时θ的值．‎ ‎22设是等差数列，是等比数列，公比大于0，已知.‎ ‎（1）求和的通项公式；‎ ‎（2）设数列满足求.‎ ‎.‎ ‎ 2022届高二上学期第一次月考数学参考答案(理）‎ 一、选择题：(本大题共12小题，每小题5分，共60分。)‎ ADBCD DDABA BD 二:填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上)‎ 13. ‎-3. 14.7 15.m<0或m>4. 16 . 5‎ 三:解答题（本大题共5小题，12+12+12+12+12=60分．解答须写出文字说明、证明过程和演算步骤．）‎ ‎17.解：　(1)相交 .....2分 ‎ （2）异面。。。。4分 ‎(3)取CD的中点G，连接EG，F G，则AC∥F G，EG∥BD，‎ 所以相交直线EF 与EG所成的角，即为异面直线EF 与BD所成的角。‎ 又因为AC⊥BD，则F G⊥EG。‎ 在Rt△EGF 中，由EG＝F G＝AC，‎ 求得∠F EG＝45°，即异面直线EF 与BD所成的角为45°。 。。。10分 ‎18．解：(1)∵不等式ax2＋bx－1>0的解集是{x|10即为>0，‎ ‎∴>0，‎ 因此(x－2)<0，解得0)，‎ ‎∴f(x)＝sin(x＋φ)．‎ ‎∵f(x)是偶函数，∴φ＝kπ＋(k∈Z)．∴＝，‎ ‎∴＋4＝4＋π2，∴T＝2π＝，又ω>0，∴ω＝1.。。。2分 ‎，∵0≤φ≤π，∴φ＝，。。。4分 ‎∴f(x)＝sin(x＋)＝cosx.。。。6分 ‎(2)∵tanα＋＝5‎ ‎∴＋＝5，∴sinαcosα＝，。。。8分 ‎∴＝＝ ‎＝＝＝2sinαcosα＝.。。。12分 ‎.21．解：(1)△ABD的面积S1＝×1×1×sinθ＝sinθ，。。。2分 ‎△BCD的面积S2＝BD2＝(12＋12－2×1×1×cosθ)＝(1－cosθ)，。。。4分 所以四边形ABCD的面积 S＝S1＋S2＝sinθ－cosθ＋＝＋sin(0<θ<π)．。。。8分 ‎(2)由S＝＋sin(0<θ<π)知，‎ 当θ－＝，即θ＝时，四边形ABCD的面积S最大，且最大值为1＋.。。。12分 ‎22.解：（1）设等差数列的公差为，等比数列的公比为.依题意，得解得故.。。。4分 所以，的通项公式为，的通项公式为.‎ ‎（2）‎ ‎ ‎ ‎..。。。8分 记 则 ‎②−①得，.‎ 所以， ‎ ‎。。。12分