【数学】新疆维吾尔自治区喀什第二中学2019-2020学年高一4月月考试题 （解析版）

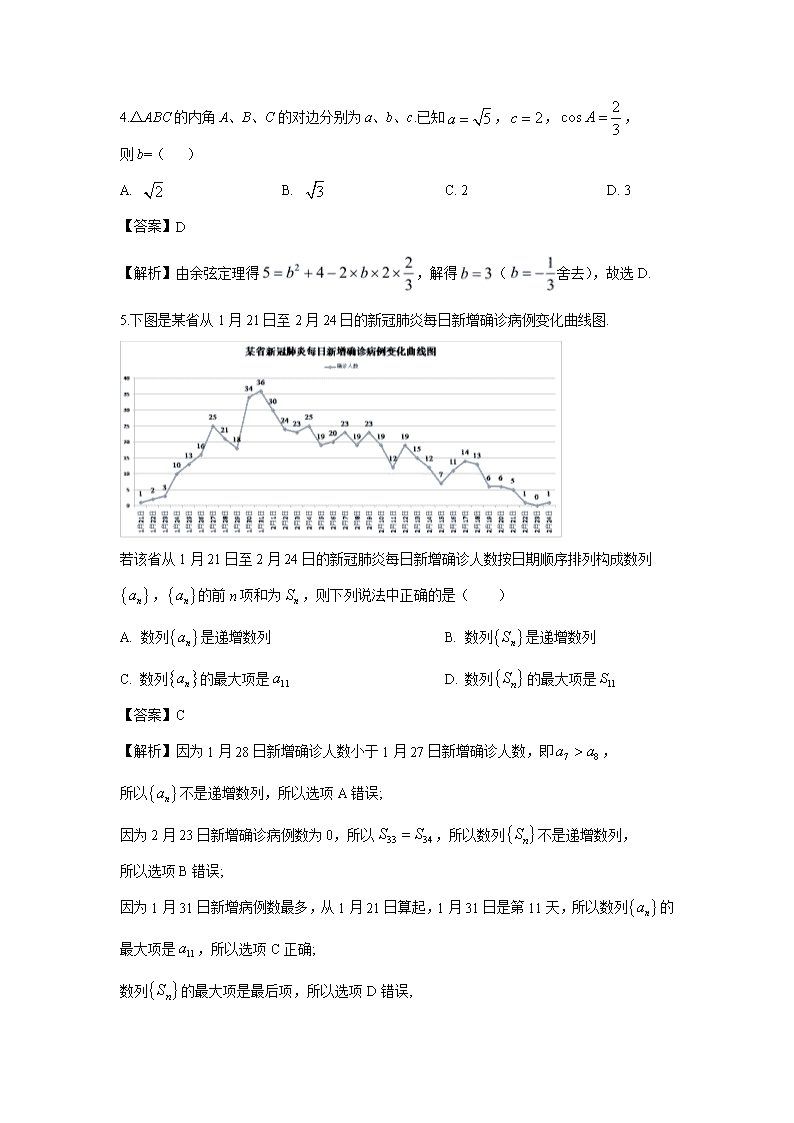
【数学】新疆维吾尔自治区喀什第二中学2019-2020学年高一4月月考试题 （解析版）

新疆维吾尔自治区喀什第二中学2019-2020学年高一 ‎4月月考数学试题 一、选择题（每小题5分，共60分）‎ ‎1.数列1，，，，，…的一个通项公式是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由于数列分母是奇数列，分子 是自然数列，故通项公式为.故选D.‎ ‎2.若，则下列结论中不恒成立的是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】因为，所以所以，即，‎ 故A，B正确.‎ 因为，所以，所以故C正确.‎ 当 时， ，故D错误.‎ 故选：D ‎3.在等差数列中，若，是方程的两根，则的前11项的和为（ ）‎ A. 22 B. ‎-33 ‎C. -11 D. 11‎ ‎【答案】D ‎【解析】等差数列{an}中，若a5，a7是方程x2－2x－6＝0的两根，‎ 则a5＋a7＝2，∴a6＝(a5＋a7)＝1，∴{an}的前11项的和为 S11＝＝‎11a6＝11×1＝11.‎ 故选D.‎ ‎4.△ABC的内角A、B、C的对边分别为a、b、c.已知，，，‎ 则b=（ ）‎ A. B. C. 2 D. 3‎ ‎【答案】D ‎【解析】由余弦定理得，解得（舍去），故选D.‎ ‎5.下图是某省从‎1月21日至‎2月24日的新冠肺炎每日新增确诊病例变化曲线图.‎ 若该省从‎1月21日至‎2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列，的前n项和为，则下列说法中正确的是（ ）‎ A. 数列是递增数列 B. 数列是递增数列 C. 数列的最大项是 D. 数列的最大项是 ‎【答案】C ‎【解析】因为‎1月28日新增确诊人数小于‎1月27日新增确诊人数，即，‎ 所以不是递增数列，所以选项A错误;‎ 因为‎2月23日新增确诊病例数为0，所以，所以数列不是递增数列，‎ 所以选项B错误;‎ 因为‎1月31日新增病例数最多，从‎1月21日算起，‎1月31日是第11天，所以数列的最大项是，所以选项C正确;‎ 数列的最大项是最后项，所以选项D错误,‎ 故选：C.‎ ‎6.设的内角所对的边分别为，若，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由正弦定理得，∴．‎ 又，∴为锐角，∴．故选B．‎ ‎7.下列函数中，最小值为4的是（）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】由题意，A中，当时，，不满足题意；‎ B中，当时，，当且仅当时，‎ 即时取得等号，而，所以函数，不满足题意；‎ C中，由，所以，当且仅当时，即，‎ 即取得等号，所以的最小值为4，满足题意；‎ D中，当时，，所以，不满足题意；‎ 故选C.‎ ‎8.已知实数，若，则的最小值是（ ）‎ A. B. C. 4 D. 8‎ ‎【答案】D ‎【解析】实数，‎ 则,‎ 当且仅当时取等号.‎ 故本题正确答案是 ‎ ‎9.设x，y满足约束条件则z=x+y的最大值为（ ）‎ A. 0 B. ‎1 ‎C. 2 D. 3‎ ‎【答案】D ‎【解析】如图，作出不等式组表示的可行域，则目标函数经过时z取得最大值，故，故选D．‎ ‎10.等差数列{an}的前n项和为Sn，且S10＝20，S20＝15，则S30＝（ ）‎ A. 10 B. C. D. 25‎ ‎【答案】C ‎【解析】由题意知：，，成等差数列 ‎，即，解得：‎ 故选C ‎11.已知数列满足: ，，设数列的前项和为，‎ 则（ ）‎ A. 1007 B. 1008 C. 1009.5 D. 1010‎ ‎【答案】D ‎【解析】由题意，数列满足: ，，‎ 可得，‎ 可得数列是以3为周期的数列，且 所以.‎ 故选：D.‎ ‎12.在中，角A、B、C所对的边分别为a、b、c，且若，则的形状是（）‎ A. 等腰三角形 B. 直角三角形 ‎ C. 等边三角形 D. 等腰直角三角形 ‎【答案】C ‎【解析】在△ABC中，角A、B、C所对的边分别为a、b、c，‎ 且b2+c2＝a2+bc．则：，‎ 由于：0＜A＜π，故：A．‎ 由于：sinBsinC＝sin‎2A，利用正弦定理得：bc＝a2，‎ 所以：b2+c2﹣2bc＝0，故：b＝c，‎ 所以：△ABC为等边三角形．故选C．‎ 二、填空题（每小题5分，共20分）‎ ‎13.不等式的解是____________‎ ‎【答案】‎ ‎【解析】因为不等式，所以，‎ 所以，所以，解得，‎ 所以不等式的解集为 .故答案为：‎ ‎14.已知数列的前n项和，则__________‎ ‎【答案】，（）‎ ‎【解析】当时，，‎ 当时，，‎ 时，不适合，‎ 所以，，（），‎ 故答案为：，（）.‎ ‎15.的内角的对边分别为，若，则 ________．‎ ‎【答案】 ‎ ‎【解析】由2bcosB＝acosC＋ccosA及正弦定理，得2sinBcosB＝sinAcosC＋sinCcosA.‎ ‎∴2sinBcosB＝sin(A＋C)．‎ 又A＋B＋C＝π，∴A＋C＝π－B.∴2sinBcosB＝sin(π－B)＝sinB.‎ 又sinB≠0，∴cosB＝.∴B＝.‎ ‎∵在△ABC中，acosC＋ccosA＝b，∴条件等式变为2bcosB＝b，∴cosB＝.‎ 又0

查看更多