人教版高三数学总复习课时作业45

人教版高三数学总复习课时作业45

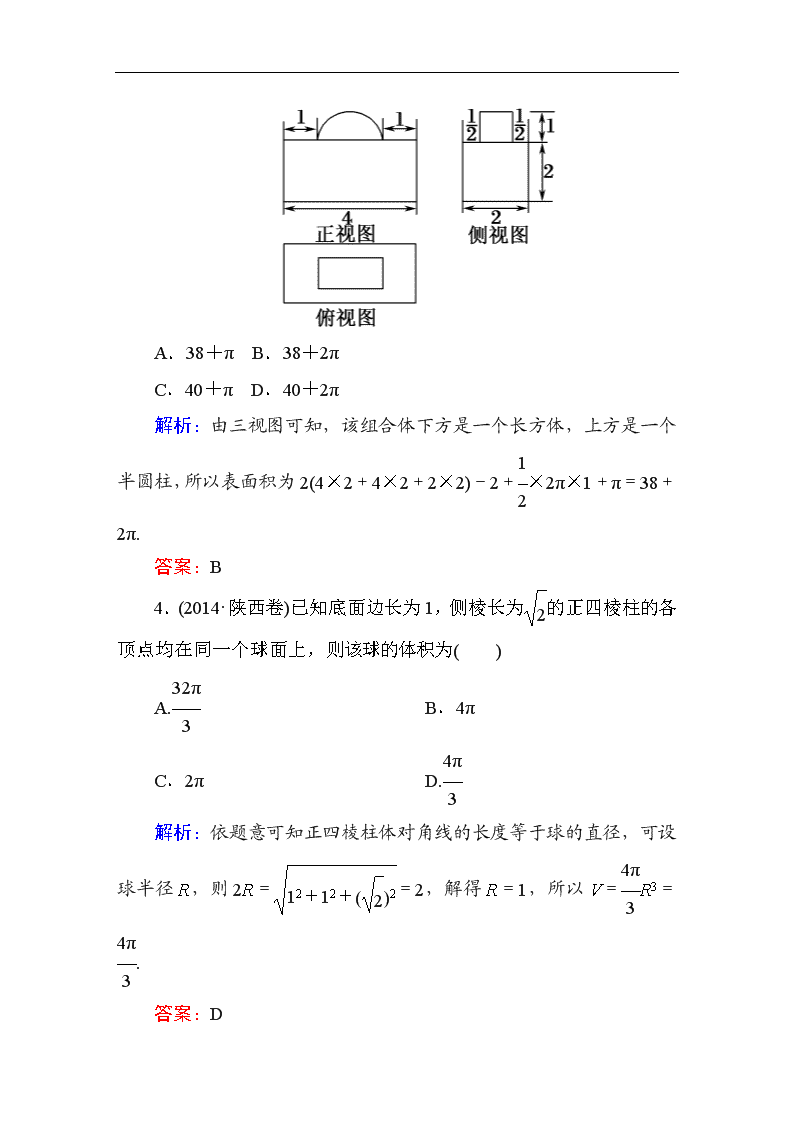
课时作业45　空间几何体的表面积与体积 一、选择题 ‎1．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为(　　)‎ A．7 B．6‎ C．5 D．3‎ 解析：设圆台较小底面半径为r，则另一底面半径为3r.‎ 由S＝π(r＋3r)·3＝84π，解得r＝7.‎ 答案：A ‎2．设一个球的表面积为S1，它的内接正方体的表面积为S2，则的值等于(　　)‎ A. B. C. D. 解析：设球的半径为R，其内接正方体的棱长为a，则易知R2＝a2，即a＝R，则＝＝.‎ 答案：D ‎3．某几何体的三视图如图所示，则其表面积为(　　)‎ A．38＋π B．38＋2π C．40＋π D．40＋2π 解析：由三视图可知，该组合体下方是一个长方体，上方是一个半圆柱，所以表面积为2(4×2＋4×2＋2×2)－2＋×2π×1＋π＝38＋2π.‎ 答案：B ‎4．(2014·陕西卷)已知底面边长为1，侧棱长为的正四棱柱的各顶点均在同一个球面上，则该球的体积为(　　)‎ A. B．4π C．2π D. 解析：依题意可知正四棱柱体对角线的长度等于球的直径，可设球半径R，则2R＝＝2，解得R＝1，所以V＝R3＝.‎ 答案：D ‎5．把一个周长为12 cm的长方形围成一个圆柱，当圆柱的体积最大时，该圆柱的底面周长与高之比为(　　)‎ A．12 B．12π C．21 D．1π 解析：设底面周长为x cm，则2πr＝x，即r＝，高为6－x，故V＝π·2(6－x)＝(6x2－x3)，则V′＝(12x－3x2)，由V′＝0得x＝4.易知当x＝4时，圆柱的体积最大，此时圆柱的底面周长是4 cm，圆柱的高为2 cm，从而底面周长与高之比为42＝21.‎ 答案：C ‎6．(2014·新课标全国卷Ⅱ)如右图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm，高为6 cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为(　　)‎ A. B. C. D. 解析：由三视图可知切削得到的零件是由两个圆柱组成的一个组合体，一个是底面半径为2，高为4的圆柱，一个是底面半径为3，高为2的圆柱，于是零件的体积V1＝πrh1＋πrh2＝π×22×4＋π×32×2＝34π，而原来毛坯的体积V＝πr2h＝π×32×‎ ‎6＝54π，所以切削掉部分的体积与原来毛坯体积的比值之比＝＝＝，故选C.‎ 答案：C 二、填空题 ‎7．若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的体积为________．‎ 解析：设圆锥底面半径为r，母线长为l，高为h，‎ 则∴∴h＝.‎ ‎∴V圆锥＝π×12×＝π.‎ 答案：π ‎8．(2014·江苏卷)设甲、乙两个圆柱的底面积分别为S1，S2，体积分别为V1，V2.若它们的侧面积相等，且＝，则的值是________．‎ 解析：设甲、乙两个圆柱的底面和高分别为r1、h1，r2、h2；由题意知2πr1h1＝2πr2h2，＝，又＝＝，所以＝，从而＝＝·＝·＝＝.‎ 答案： ‎9．已知三棱锥O—ABC中，∠BOC＝90°，OA⊥平面BOC，其中AB＝AC＝，BC＝，O，A，B，C四点均在球S的表面上，则球S的表面积为________．‎ 解析：易知以O点为顶点的三条棱两两垂直，则球S即为以O为顶点，以OA，OB，OC为棱的长方体的外接球，所以2R＝‎ ＝×＝(R为球S的半径)，所以R＝，表面积S＝4πR2＝.‎ 答案： 三、解答题 ‎10．一个几何体的三视图如图所示．已知正视图是底边长为1的平行四边形，侧视图是一个长为，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．‎ ‎(1)求该几何体的体积V；‎ ‎(2)求该几何体的表面积S.‎ 解：‎ ‎(1)由三视图可知，该几何体是一个平行六面体(如图)，其底面是边长为1的正方形，高为.‎ 所以V＝1×1×＝.‎ ‎(2)由三视图可知，该平行六面体中，A1D⊥平面ABCD，CD⊥平面BCC1B1，所以AA1＝2，侧面ABB1A1，CDD1C1均为矩形，所以S＝2×(1×1＋1×＋1×2)＝6＋2.‎ ‎11．如图，在直三棱柱ABC—A1B1C1中，AB＝AC＝5，BB1＝BC＝6，D，E分别是AA1和B1C的中点．‎ ‎(1)求证：DE∥平面ABC；‎ ‎(2)求三棱锥E—BCD的体积．‎ 解：(1)‎ 证明：如图，取BC的中点G，连接AG，EG，因为E是B1C的中点，所以EG∥BB1，且EG＝BB1.‎ 由题意知，AA1綊BB1.‎ 而D是AA1的中点，所以EG綊AD.‎ 所以四边形EGAD是平行四边形．‎ 所以ED∥AG.‎ 又DE⊄平面ABC，AG⊂平面ABC，‎ 所以DE∥平面ABC.‎ ‎(2)因为AD∥BB1，所以AD∥平面BCE.‎ 所以VE—BCD＝VD—BCE＝VA—BCE＝VE—ABC.‎ 由(1)知，DE∥平面ABC，‎ 所以VE—BCD＝VE—ABC＝VD—ABC＝AD·BC·AG＝×3×6×4＝12.‎ ‎1．(2014·湖南卷)一块石材表示的几何体的三视图如下图所示．将该石材切削、打磨，加工成球，则能得到的最大球的半径等于(　　)‎ A．1　　　　B．2　　　　C．3　　　　D．4‎ 解析：‎ 由三视图可得原石材为如右图所示的直三棱柱A1B1C1—ABC，且AB＝8，BC＝6，BB1＝12.‎ 若要得到半径最大的球，则此球与平面A1B1BA，BCC1B1，ACC1A1相切，故此时球的半径与△ABC内切圆的半径相等，故半径r＝＝2.故选B.‎ 答案：B ‎2．(2014·湖北卷)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也．又以高乘之，三十六成一．该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式V≈L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么，近似公式V≈L2h相当于将圆锥体积公式中的π近似取为(　　)‎ A. B. C. D. 解析：借助圆锥的体积公式，底面圆的面积、周长公式求解．设圆锥的底面圆半径为r，则圆锥的底面圆周长L＝2πr ‎，所以圆锥底面圆的半径r＝，则圆锥的体积为V＝Sh＝πr2h＝π·h＝L2h.又V≈L2h，所以L2h≈L2h，解得π≈.‎ 答案：B ‎3．如图，在三棱锥D—ABC中，已知BC⊥AD，BC＝2，AD＝6，AB＋BD＝AC＋CD＝10，则三棱锥D—ABC的体积的最大值是________．‎ ‎ ‎ 　 解析：由题意知，线段AB＋BD与线段AC＋CD的长度是定值，因为棱AD与棱BC相互垂直．‎ 设d为AD到BC的距离．‎ 则VD—ABC＝AD·BC×d××＝2d，‎ 当d最大时，VD—ABC体积最大，‎ ‎∵AB＋BD＝AC＋CD＝10，‎ ‎∴当AB＝BD＝AC＝CD＝5时，‎ d有最大值＝.‎ 此时V＝2.‎ 答案：2 ‎4．如图所示，从三棱锥P—ABC的顶点P沿着三条侧棱PA，PB，PC剪开成平面图形得到△P1P2P3，且P2P1＝P2P3.‎ ‎(1)在三棱锥P—ABC中，求证：PA⊥BC.‎ ‎(2)若P1P2＝26，P1P3＝20，求三棱锥P—ABC的体积．‎ 解：‎ ‎(1)证明：由题设知A，B，C分别是P1P3，P1P2，P2P3的中点，且P2P1＝P2P3.‎ 从而PB＝PC，AB＝AC，‎ 取BC的中点D，连AD，PD，‎ 则AD⊥BC，PD⊥BC，AD∩PD＝D，‎ ‎∴BC⊥平面PAD.‎ ‎∵PA⊂平面PAD，故PA⊥BC.‎ ‎(2)由题设有 AB＝AC＝P1P2＝13，PA＝P1A＝BC＝10，‎ PB＝PC＝P1B＝13，‎ ‎∴AD＝PD＝＝12，‎ 在等腰三角形DPA中，‎ 底边PA上的高h＝＝，‎ ‎∴S△DPA＝PA·h＝5.‎ 又BC⊥平面PAD，‎ ‎∴VP—ABC＝VB—PDA＋VC—PDA ‎＝BD·S△DPA＋DC·S△PDA ‎＝BC·S△PDA＝×10×5＝.‎