高中数学第一单元常用逻辑用语1_3_2命题的四种形式教学案新人教B版选修1-1
1.3.2 命题的四种形式
学习目标 1.了解四种命题的概念,会写出所给命题的逆命题、否命题和逆否命题.2.认识
四种命题之间的关系以及真假性之间的联系.3.会利用命题的等价性解决问题.
知识点一 四种命题的概念
思考 给出以下四个命题:
(1)当 x=2 时,x2-3x+2=0;
(2)若 x2-3x+2=0,则 x=2;
(3)若 x≠2,则 x2-3x+2≠0;
(4)若 x2-3x+2≠0,则 x≠2.
你能说出命题(1)与其他三个命题的条件与结论有什么关系吗?
梳理 对命题的条件和结论进行“换位”和“换质”(否定)后,可以构成四种不同形式的命
题:
(1)原命题:________________;
(2)逆命题:________________(“换位”);
(3)否命题:________________(“换质”);
(4)逆否命题:________________(“换位”又“换质”).
知识点二 命题的四种形式之间的关系
思考 1 为了书写方便常把 p 与 q 的否定分别记作“綈 p”和“綈 q”,如果原命题是“如果
p,则 q”,那么它的逆命题、否命题、逆否命题该如何表示?
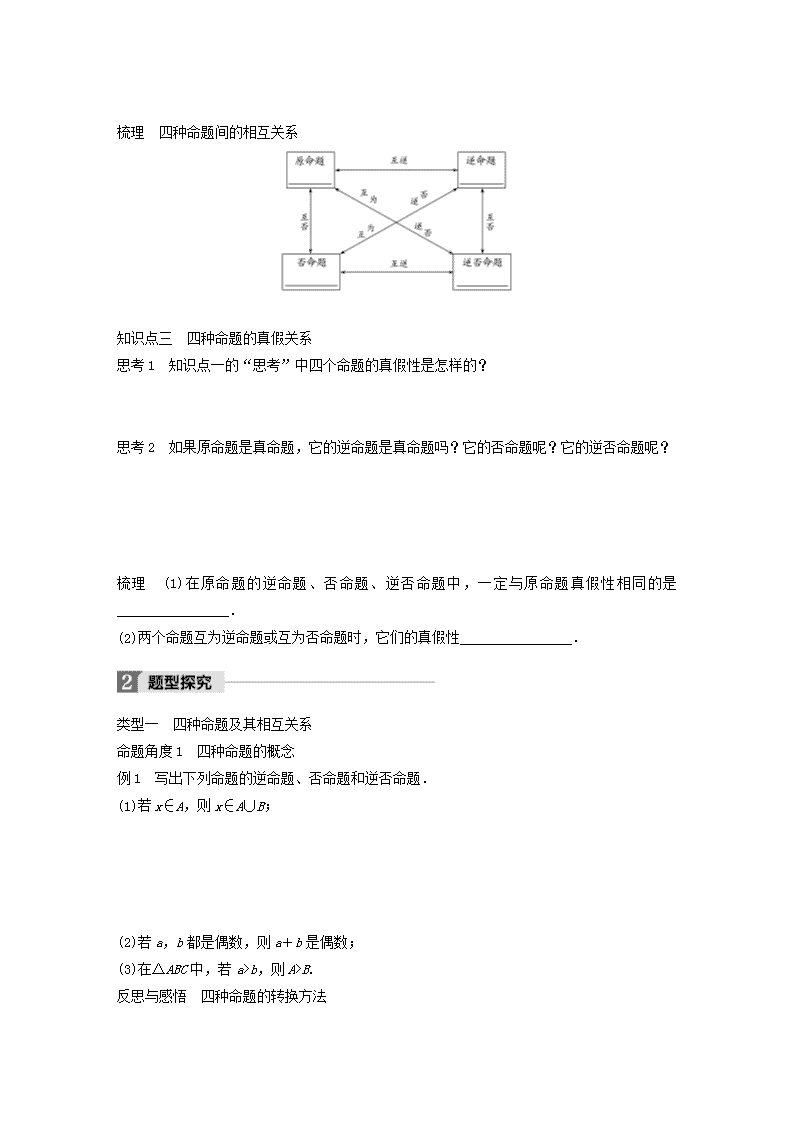
思考 2 原命题的否命题与原命题的逆否命题之间是什么关系?原命题的逆命题与其逆否命
题之间是什么关系?原命题的逆命题与其否命题呢?
梳理 四种命题间的相互关系
知识点三 四种命题的真假关系
思考 1 知识点一的“思考”中四个命题的真假性是怎样的?
思考 2 如果原命题是真命题,它的逆命题是真命题吗?它的否命题呢?它的逆否命题呢?
梳理 (1)在原命题的逆命题、否命题、逆否命题中,一定与原命题真假性相同的是
________________.
(2)两个命题互为逆命题或互为否命题时,它们的真假性________________.
类型一 四种命题及其相互关系
命题角度 1 四种命题的概念
例 1 写出下列命题的逆命题、否命题和逆否命题.
(1)若 x∈A,则 x∈A∪B;
(2)若 a,b 都是偶数,则 a+b 是偶数;
(3)在△ABC 中,若 a>b,则 A>B.
反思与感悟 四种命题的转换方法
(1)交换原命题的条件和结论,所得命题是原命题的逆命题.
(2)同时否定原命题的条件和结论,所得命题是原命题的否命题.
(3)交换原命题的条件和结论,并且同时否定,所得命题是原命题的逆否命题.
跟踪训练 1 命题“若函数 f(x)=logax(a>0,a≠1)在其定义域内是减函数,则 loga2<0”的
逆否命题是( )
A.若 loga2<0,则函数 f(x)=logax(a>0,a≠1)在其定义域内不是减函数
B.若 loga2≥0,则函数 f(x)=logax(a>0,a≠1)在其定义域内不是减函数
C.若 loga2<0,则函数 f(x)=logax(a>0,a≠1)在其定义域内是减函数
D.若 loga2≥0,则函数 f(x)=logax(a>0,a≠1)在其定义域内是减函数
命题角度 2 四种命题的相互关系
例 2 若命题 p:“若 x+y=0,则 x,y 互为相反数”的否命题为 q,命题 q 的逆命题为 r,
则 r 与 p 的逆命题的关系是( )
A.互为逆命题
B.互为否命题
C.互为逆否命题
D.同一命题
反思与感悟 判断四种命题之间四种关系的两种方法
(1)利用四种命题的定义判断;
(2)巧用“逆、否”两字进行判断,如“逆命题”与“逆否命题”中不同有“否”一个字,是
互否关系;而“逆命题”与“否命题”中不同有“逆、否”二字,其关系为逆否关系.
跟踪训练 2 已知命题 p 的逆命题是“若实数 a,b 满足 a=1 且 b=2,则 a+b<4”,则命题
p 的否命题是__________________________________.
类型二 四种命题的真假判断
例 3 有以下命题:
①“若 xy=1,则 x,y 互为倒数”的逆命题;②“面积相等的三角形全等”的否命题;③“若
m≤1,则 x2-2x+m=0 有实数解”的逆否命题;④“若 A∩B=B,则 A⊆B”的逆否命题,其
中真命题为( )
A.①② B.②③
C.④ D.①②③
反思与感悟 原命题与逆否命题总是具有相同的真假性,与逆命题或否命题的真假性没有关
系.逆命题与否命题也总是具有相同的真假性.
跟踪训练 3 命题“若 a>b,则 ac2>bc2(a,b,c∈R)”与它的逆命题、否命题、逆否命题中,
真命题的个数为( )
A.0 B.2 C.3 D.4
类型三 等价命题的应用
例 4 判断命题“已知 a,x 为实数,若关于 x 的不等式 x2+(2a+1)x+a2+2≤0 的解集非空,
则 a≥1”的逆否命题的真假.
引申探究
判断命题“已知 a,x 为实数,若关于 x 的不等式 x2+(2a+1)x+a2+2>0 的解集为 R,则 a<7
4
”
的逆否命题的真假.
反思与感悟 由于原命题和它的逆否命题有相同的真假性,即互为逆否命题的两个命题具有
等价性,所以我们在直接证明某一个命题为真命题有困难时,可以通过证明它的逆否命题为
真命题来间接地证明原命题为真命题.
跟踪训练 4 证明:若 a2-4b2-2a+1≠0,则 a≠2b+1.
1.命题“若 a∉ A,则 b∈B”的否命题是( )
A.若 a∉ A,则 b∉ B B.若 a∈A,则 b∉ B
C.若 b∈B,则 a∉ A D.若 b∉ B,则 a∉ A
2.命题“如果 x2<1,则-1
1 或 x<-1,则 x2>1
D.如果 x≥1 或 x≤-1,则 x2≥1
3.如果一个命题的否命题是真命题,那么这个命题的逆命题是( )
A.真命题
B.假命题
C.不一定是真命题
D.不一定是假命题
4.下列命题:
①“全等三角形的面积相等”的逆命题;
②“正三角形的三个内角均为 60°”的否命题;
③“若 k<0,则方程 x2+(2k+1)x+k=0 必有两相异实数根”的逆否命题.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
5.已知命题“若 m-10,则 C>0.
其中正确结论的个数是( )
A.1 B.2
C.3 D.4
类型二 逻辑联结词与量词的综合应用
例 2 已知 p:∃x∈R,mx2+2≤0.q:∀x∈R,x2-2mx+1>0,若 p∨q 为假命题,则实数 m
的取值范围是( )
A.[1,+∞) B.(-∞,-1]
C.(-∞,-2] D.[-1,1]
反思与感悟 解决此类问题首先理解逻辑联结词的含义,掌握简单命题与含有逻辑联结词的
命题的真假关系.其次要善于利用等价关系,如:p 真与綈 p 假等价,p 假与綈 p 真等价,将
问题转化,从而谋得最佳解决途径.
跟踪训练 2 已知命题 p:方程 2x2+ax-a2=0 在[-1,1]上有解;命题 q:只有一个实数 x0
满足不等式 x2
0+2ax0+2a≤0.若命题“p 或 q”是假命题,求 a 的取值范围.
类型三 充分条件与必要条件
命题角度 1 充分条件与必要条件的判断
例 3 (1)设 x∈R,则“x2-3x>0”是“x>4”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
(2)已知 a,b 是实数,则“a>0 且 b>0”是“a+b>0 且 ab>0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
反思与感悟 条件的充要关系的常用判断方法
(1)定义法:直接判断若 p 则 q,若 q 则 p 的真假.
(2)等价法:利用 A⇒B 与綈 B⇒綈 A,B⇒A 与綈 A⇒綈 B,A⇔B 与綈 B⇔綈 A 的等价关系,对
于条件或结论是否定式的命题,一般运用等价法.
(3)利用集合间的包含关系判断:若 A⊆B,则 A 是 B 的充分条件或 B 是 A 的必要条件;若 A
=B,则 A 是 B 的充要条件.
跟踪训练 3 使 a>b>0 成立的一个充分不必要条件是( )
A.a2>b2>0 B. 1
2
log a > 1
2
log b >0
C.ln a>ln b>0 D.xa>xb 且 x>0.5
命题角度 2 充分条件与必要条件的应用
例 4 设命题 p:x2-5x+6≤0;命题 q:(x-m)(x-m-2)≤0,若綈 p 是綈 q 的必要不充分
条件,求实数 m 的取值范围.
反思与感悟 利用条件的充要性求参数的范围
(1)解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据
集合之间的关系列出关于参数的不等式求解.
(2)注意利用转化的方法理解充分必要条件:若綈 p 是綈 q 的充分不必要(必要不充分、充要)
条件,则 p 是 q 的必要不充分(充分不必要、充要)条件.
跟踪训练 4 已知 p:2x2-9x+a<0,q:20,总有(x+1)ex>1,则綈 p 为( )
A.∃x≤0,使得(x+1)ex≤1
B.∃x>0,使得(x+1)ex≤1
C.∀x>0,总有(x+1)ex≤1
D.∀x≤0,总有(x+1)ex≤1
2.设 x,y∈R,则“x≥2 且 y≥2”是“x2+y2≥4”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.“若 x,y 全为零,则 xy=0”的否命题为______________.
4.已知命题 p:若 x>y,则-x<-y;命题 q:若 x>y,则 x2>y2.在命题①p∧q;②p∨q;③p∧(綈
q);④(綈 p)∨q 中,真命题是________.
5.对任意 x∈[-1,2],x2-a≥0 恒成立,则实数 a 的取值范围是________.
1.否命题和命题的否定是两个不同的概念
(1)否命题是将原命题的条件否定作为条件,将原命题的结论否定作为结论构造一个新的命
题.
(2)命题的否定只是否定命题的结论,常用于反证法.若命题为“如果 p,则 q”,则该命题
的否命题是“如果綈 p,则綈 q”;命题的否定为“如果 p,则綈 q”.
2.四种命题的三种关系,互否关系,互逆关系,互为逆否关系,只有互为逆否关系的命题是
等价命题.
3.判断 p 与 q 之间的关系时,要注意 p 与 q 之间关系的方向性,充分条件与必要条件方向正
好相反,不要混淆.
4.注意常见逻辑联结词的否定
一些常见逻辑联结词的否定要记住,如:“都是”的否定“不都是”,“全是”的否定“不
全是”,“至少有一个”的否定“一个也没有”,“至多有一个”的否定“至少有两个”.
答案精析
问题导学
知识点一
思考 命题(1)的条件和结论与命题(2)的条件和结论恰好互换了.命题(1)的条件与结论恰好
是命题(3)条件的否定和结论的否定.命题(1)的条件和结论恰好是命题(4)结论的否定和条件
的否定.
梳理 (1)如果 p,则 q (2)如果 q,则 p (3)如果綈 p,则綈 q (4)如果綈 q,则綈 p
知识点二
思考 1 逆命题:如果 q,则 p.否命题:如果綈 p,则綈 q.逆否命题:如果綈 q,则綈 p.
思考 2 互逆、互否、互为逆否.
梳理 如果 p,则 q 如果 q,则 p 如果綈 p,则綈 q 如果綈 q,则綈 p
知识点三
思考 1 (1)真命题,(2)假命题,(3)假命题,(4)真命题.
思考 2 原命题为真,其逆命题不一定为真,其否命题不一定为真,其逆否命题一定是真命
题.
梳理 (1)逆否命题 (2)没有关系
题型探究
例 1 解 (1)逆命题:若 x∈A∪B,
则 x∈A.
否命题:若 x∉ A,则 x∉ A∪B.
逆否命题:若 x∉ A∪B,则 x∉ A.
(2)逆命题:若 a+b 是偶数,则 a,b 都是偶数.
否命题:a,b 不都是偶数,则 a+b 不是偶数.
逆否命题:若 a+b 不是偶数,则 a,b 不都是偶数.
(3)逆命题:在△ABC 中,若 A>B,则 a>b.
否命题:在△ABC 中,若 a≤b,则 A≤B.
逆否命题:在△ABC 中,若 A≤B,
则 a≤b.
跟踪训练 1 B
例 2 B [已知命题 p:若 x+y=0,
则 x,y 互为相反数.
命题 p 的否命题 q 为:若 x+y≠0,
则 x,y 不互为相反数,
命题 q 的逆命题 r 为:
若 x,y 不互为相反数,则 x+y≠0,
∴r 是 p 的逆否命题,
∴r 是 p 的逆命题的否命题,故选 B.]
跟踪训练 2 若实数 a,b 满足 a+b≥4,则 a≠1 或 b≠2
解析 由命题 p 的逆命题与其否命题互为逆否命题可得.
例 3 D [①②③显然正确;对于④,若 A∩B=B,则 B⊆A,
所以原命题为假,故它的逆否命题也为假.]
跟踪训练 3 B [命题“若 a>b,
则 ac2>bc2(a,b,c∈R)”是假命题,
则其逆否命题是假命题.
该命题的逆命题为“若 ac2>bc2,
则 a>b(a,b,c∈R)”是真命题,
则其否命题是真命题.故选 B.]
例 4 解 方法一 原命题的逆否命题:已知 a,x 为实数,若 a<1,则关于 x 的不等式 x2+(2a
+1)x+a2+2≤0 的解集为∅ ,判断如下:
抛物线 y=x2+(2a+1)x+a2+2 的开口向上,
令 x2+(2a+1)x+a2+2=0,
则Δ=(2a+1)2-4(a2+2)=4a-7.
因为 a<1,所以 4a-7<0,
即关于 x 的不等式 x2+(2a+1)x+a2+2≤0 的解集为∅ .故此命题为真命题.
方法二 利用原命题的真假去判断逆否命题的真假.
因为关于 x 的不等式 x2+(2a+1)x+a2+2≤0 的解集非空,
所以(2a+1)2-4(a2+2)≥0,
即 4a-7≥0,解得 a≥7
4
≥1,
所以原命题为真,故其逆否命题为真.
引申探究
解 先判断原命题的真假如下:
因为 a,x 为实数,关于 x 的不等式 x2+(2a+1)x+a2+2>0 的解集为 R,且抛物线 y=x2+(2a
+1)x+a2+2 的开口向上,
所以Δ=(2a+1)2-4(a2+2)
=4a-7<0,
所以 a<7
4
.所以原命题是真命题.
因为互为逆否命题的两个命题同真同假,
所以原命题的逆否命题为真命题.
跟踪训练 4 证明 “若 a2-4b2-2a+1≠0,则 a≠2b+1”的逆否命题为“若 a=2b+1,则
a2-4b2-2a+1=0”.
∵a=2b+1,
∴a2-4b2-2a+1=(2b+1)2-4b2-2(2b+1)+1
=4b2+1+4b-4b2-4b-2+1=0.
∴命题“若 a=2b+1,
则 a2-4b2-2a+1=0”为真命题.
由原命题与逆否命题具有相同的真假性可知,结论正确.
当堂训练
1.B 2.D 3.A 4.C 5.[1,2]