- 2021-06-24 发布 |
- 37.5 KB |
- 9页

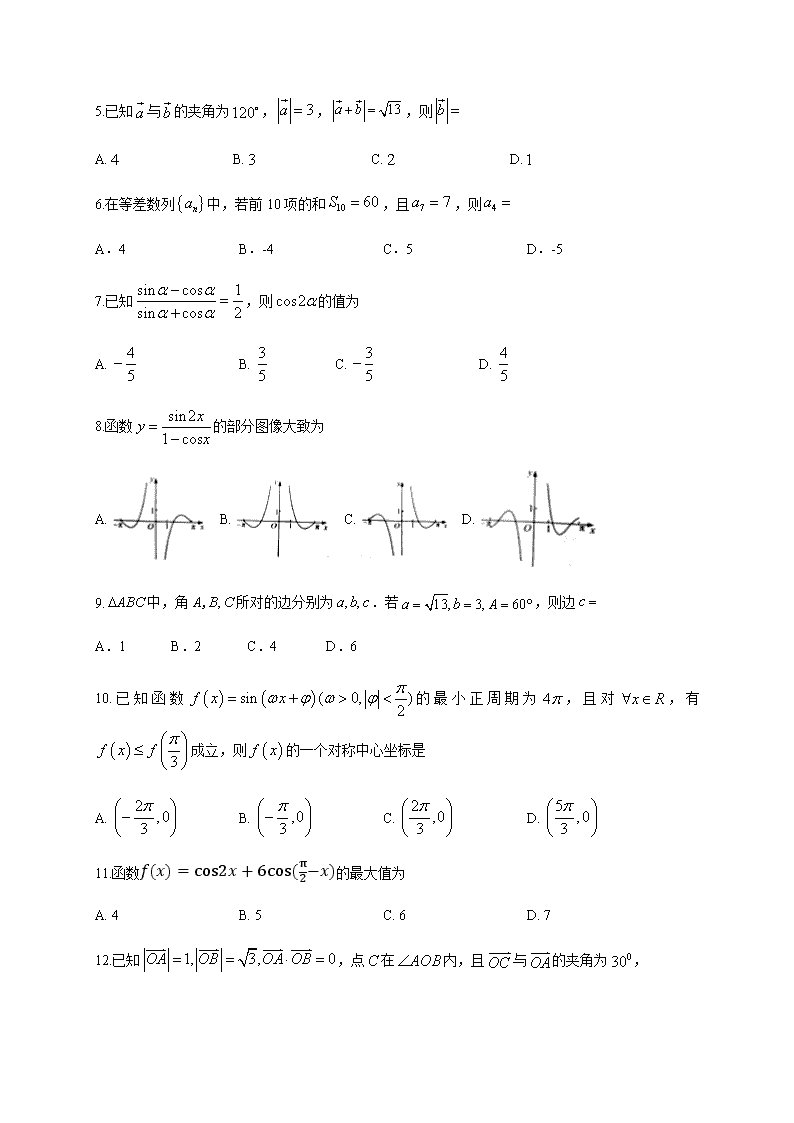

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
四川省宜宾市叙州区第二中学校2019-2020学年高一下学期第四学月考试数学(文)试题
2020年春四川省宜宾市叙州区第二中学高一第四学月考试 文科数学试题 注意事项: 1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。 2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。 3.考试结束后,将本试卷和答题卡一并交回。 第I卷 选择题(60分) 一、选择题:本题共12小题,每小题5分,共60分。在每小题给的四个选项中,只有一项是符合题目要求的。 1.化成弧度制为 A. B. C. D. 2.sin11π3的值为 A. -32 B. -12 C. 12 D. 32 3.为了得到函数y=sin(2x−π3)的图象,只需把函数y=sin2x的图象上所有的点 A. 向左平行移动π3个单位长度 B. 向右平行移动π3个单位长度 C. 向左平行移动π6个单位长度 D. 向右平行移动π6个单位长度 4.下列函数中是奇函数,且最小正周期是π的函数是 A. y=tan2x B. y=sinx C. y=sinπ2+2x D. y=cos3π2−2x 5.已知与的夹角为,,,则 A. B. C. D. 6.在等差数列中,若前10项的和,且,则 A.4 B.-4 C.5 D.-5 7.已知,则的值为 A. B. C. D. 8.函数的部分图像大致为 A. B. C. D. 9.中,角所对的边分别为.若,则边 A.1 B.2 C.4 D.6 10.已知函数的最小正周期为,且对,有成立,则的一个对称中心坐标是 A. B. C. D. 11.函数f(x)=cos2x+6cos(π2−x)的最大值为 A. 4 B. 5 C. 6 D. 7 12.已知,点在内,且与的夹角为, 设,则的值为 A. B. C. D. 第II卷 非选择题(90分) 二、填空题:本题共4小题,每小题5分,共20分。 13.已知向量,,且,则的值为________. 14.若,则________. 15.设各项都是正数的等比数列{},Sn为前n项和,且S10=10,S30=70,那么S40=______ 16.已知向量=(3,-4),=(6,-3),=(5-m,-3-m),若∠ABC为锐角,则实数m的取值范围是__. 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。 17.(10分)已知函数. (I)求函数的最小正周期; (II)求在区间上的最大值和最小值. 18.(12分)记Sn为等比数列的前n项和,已知S2=2,S3=-6. (I)求的通项公式; (II)求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列。 19.(12分)在ΔABC中,角A,B,C的对边分别为a,b,c,a=8,c−13b=acosB. (I)若ΔABC有两解,求b的取值范围; (II)若ΔABC的面积为82,B>C,求b−c的值. 20.(12分)若数列{}的前n项和Sn=2-2. (I)求数列{}的通项公式; (II)若bn=•log,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)<0恒成立,试求实数m的取值范围. 21.(12分)已知函数f(x)=2x−a2x(a∈R). (I)若f(x)在[1,2]上是减函数,求a的取值范围; (II)设a=−1,g(x)=f(x)−m⋅2x+43m,若函数g(x)有且只有一个零点,求实数m的取值范围. 22.(12分)已知a→=(1−cosx,2sinx2),b→=(1+cosx,2cosx2) (I)若f(x)=2+sinx−14|a→−b→|2,求f(x)的表达式; (II)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式; (III)若h(x)=g(x)−λf(x)+1在[−π2,π2]上是增函数,求实数l的取值范围. 2020年春四川省宜宾市叙州区第二中学高一第四学月考试 文科数学试题答案 1-5:AADDA 6-10:CACCA 11-12:BC 13. 14. 15.150 16. 17.1, 因此,函数的最小正周期为; (2),, 当时,函数取得最小值; 当时,函数取得最大值. 18.(1)设的公比为.由题设可得 ,解得, . 故的通项公式为. (2)由(1)可得. 由于, 故, , 成等差数列. 点睛:等差、等比数列的性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形.在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法. 19.(1)∵c-13b=acosB,∴sinC-13sinB=sinAcosB, ∴sinAcosB+sinBcosA-13sinB=sinAcosB.即sinBcosA=13sinB ∵sinB≠0,∴cosA=13,∴sinA=223.若ΔABC有两解,∴bsinA<8查看更多