2014年高考数学(理科)真题分类汇编E单元 不等式
数 学
E单元 不等式
E1 不等式的概念与性质
5.B6,B7,E1[2014·山东卷] 已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
A. > B. ln(x2+1)>ln(y2+1)
C. sin x>sin y D. x3>y3
5.D [解析] 因为ax<ay(0<a<1),所以x>y,所以sin x>sin y,ln(x2+1)>ln(y2+1),>都不一定正确,故选D.
4.E1[2014·四川卷] 若a>b>0,c
B.<
C.> D.<
4.D [解析] 因为c<d<0,所以<<0,即->->0,与a>b>0对应相乘得,->->0,所以<.故选D.
E2 绝对值不等式的解法
9.E2、E8[2014·安徽卷] 若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为( )
A.5或8 B.-1或5
C.-1或-4 D.-4或8
9.D [解析] 当a≥2时,
f(x)=
由图可知,当x=-时,fmin(x)=f=-1=3,可得a=8.
当a<2时,f(x)
由图可知,当x=-时,fmin(x)=f=-+1=3,可得a=-4.综上可知,a的值为-4或8.
E3 一元二次不等式的解法
2.A1、E3[2014·全国卷] 设集合M={x|x2-3x-4<0},N={x|0≤x≤5},则M∩N=( )
A.(0,4] B.[0,4)
C.[-1,0) D.(-1,0]
2.B [解析] 因为M={x|x2-3x-4<0}={x|-14,解得m>2或m<-2,故m的取值范围是(-∞,-2)∪(2,+∞).
E4 简单的一元高次不等式的解法
E5 简单的线性规划问题
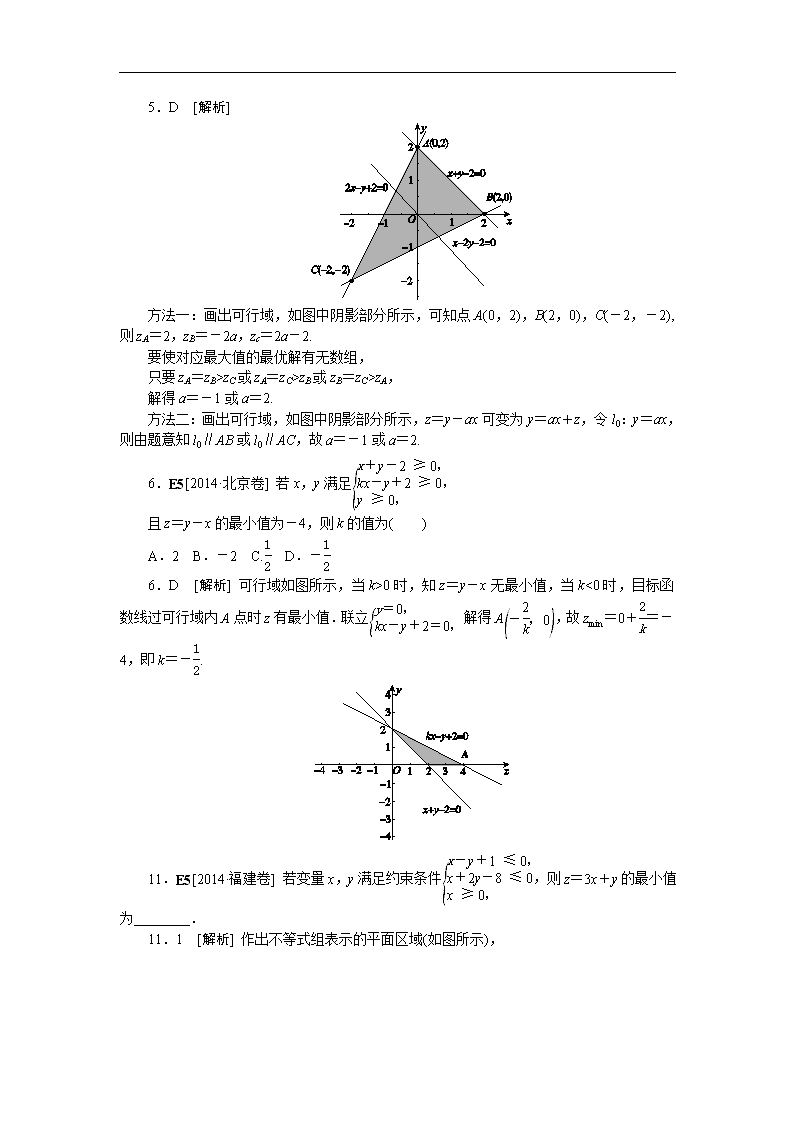
5.E5[2014·安徽卷] x,y满足约束条件若z=y-ax取得最大值的最优解不唯一,则实数a的值为( )
A.或-1 B.2或
C.2或1 D.2或-1
5.D [解析]
方法一:画出可行域,如图中阴影部分所示,可知点A(0,2),B(2,0),C(-2,-2), 则zA=2,zB=-2a,zc=2a-2.
要使对应最大值的最优解有无数组,
只要zA=zB>zC或zA=zC>zB或zB=zC>zA,
解得a=-1或a=2.
方法二:画出可行域,如图中阴影部分所示,z=y-ax可变为y=ax+z,令l0:y=ax,则由题意知l0∥AB或l0∥AC,故a=-1或a=2.
6.E5[2014·北京卷] 若x,y满足
且z=y-x的最小值为-4,则k的值为( )
A.2 B.-2 C. D.-
6.D [解析] 可行域如图所示,当k>0时,知z=y-x无最小值,当k<0时,目标函数线过可行域内A点时z有最小值.联立解得A,故zmin=0+=-4,即k=-.
11.E5[2014·福建卷] 若变量x,y满足约束条件则z=3x+y的最小值为________.
11.1 [解析] 作出不等式组表示的平面区域(如图所示),
把z=3x+y变形为y=-3x+z,则当直线y=3x+z经过点(0,1)时,z最小,将点(0,1)代入z=3x+y,得zmin=1,即z=3x+y的最小值为1.
3.E5[2014·广东卷] 若变量x,y满足约束条件且z=2x+y的最大值和最小值分别为m和n,则m-n=( )
A.5 B.6
C.7 D.8
3.B [解析] 本题考查运用线性规划知识求目标函数的最值,注意利用数形结合思想求解.画出不等式组表示的平面区域,如图所示.
当目标函数线经过点A(-1,-1)时,z取得最小值;当目标函数线经过点B(2,-1)时,z取得最大值.故m=3,n=-3,所以m-n=6.
14.E5[2014·湖南卷] 若变量x,y满足约束条件且z=2x+y的最小值为-6,则k=________.
14.-2 [解析] 画出可行域,如图中阴影部分所示,不难得出z=2x+y在点A(k,k)处取最小值,即3k=-6,解得k=-2.
14.E5[2014·全国卷] 设x,y满足约束条件则z=x+4y的最大值为________.
14.5 [解析] 如图所示,满足约束条件的可行域为△ABC的内部(包括边界), z=x+4y的最大值即为直线y=-x+z的纵截距最大时z的值.结合题意,当y=-x+z经过点A时,z取得最大值.
由可得点A的坐标为(1,1),
所以zmax=1+4=5.
9.E5、A3[2014·新课标全国卷Ⅰ] 不等式组的解集记为D,有下面四个命题:
p1:∀(x,y)∈D,x+2y≥-2,
p2:∃(x,y)∈D,x+2y≥2,
p3:∀(x,y)∈D,x+2y≤3,
p4:∃(x,y)∈D,x+2y≤-1.
其中的真命题是( )
A.p2,p3 B.p1,p2
C.p1,p4 D.p1,p3
9.B [解析] 不等式组表示的区域D如图中的阴影部分所示,设目标函数z=x+2y,根据目标函数的几何意义可知,目标函数在点A(2,-1)处取得最小值,且zmin=2-2=0,即x+2y的取值范围是[0,+∞),故命题p1,p2为真,命题p3,p4为假.
9.E5[2014·新课标全国卷Ⅱ] 设x,y满足约束条件则z=2x-y的最大值为( )
A.10 B.8 C.3 D.2
9.B [解析] 已知不等式组表示的平面区域如图中的阴影部分所示,根据目标函数的几何意义可知,目标函数在点A(5,2)处取得最大值,故目标函数的最大值为2×5-2=8.
9.E5[2014·山东卷] 已知x,y满足约束条件当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2 时,a2+b2的最小值为( )
A. 5 B. 4 C. D. 2
9.B [解析] 画出约束条件表示的可行域(如图所示).
显然,当目标函数z=ax+by过点A(2,1)时,z取得最小值,即2 =2a+b,所以2 -2a=b,所以a2+b2=a2+(2 -2a)2=5a2-8 a+20,构造函数m(a)=5a2-8 a+20(>a>0),利用二次函数求最值,显然函数m(a)=5a2-8a+20的最小值是=4,即a2+b2的最小值为4.故选B.
18.F2,E5[2014·陕西卷] 在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在△ABC三边围成的区域(含边界)上.
(1)若++=0,求||;
(2)设=m+n(m,n∈R),用x,y表示m-n,并求m-n的最大值.
18.解:(1)方法一:∵++=0,
又++=(1-x,1-y)+(2-x,3-y)+(3-x,2-y)=(6-3x,6-3y),
∴解得
即=(2,2),故||=2.
方法二:∵++=0,
则(-)+(-)+(-)=0,
∴=(++)=(2,2),
∴||=2.
(2)∵=m+n,
∴(x,y)=(m+2n,2m+n),
∴
两式相减得,m-n=y-x,
令y-x=t,由图知,当直线y=x+t过点B(2,3)时,t取得最大值1,故m-n的最大值为1.
5.E5,L1[2014·四川卷] 执行如图11所示的程序框图,如果输入的x,y∈R,那么输出的S的最大值为( )
图11
A.0 B.1 C.2 D.3
5.C [解析] 题中程序输出的是在的条件下S=2x+y 的最大值与1中较大的数.结合图像可得,当x=1,y=0时,S=2x+y取得最大值2,2>1,故选C.
2.E5[2014·天津卷] 设变量x,y满足约束条件则目标函数z=x+2y的最小值为( )
A.2 B.3 C.4 D.5
2.B [解析] 画出可行域,如图所示.解方程组得即点A(1,1).
当目标函数线过可行域内A点时,目标函数有最小值,即zmin=1×1+2×1=3.
13.E5 [2014·浙江卷] 当实数x,y满足时,1≤ax+y≤4恒成立,则实数a的取值范围是________.
13. [解析] 实数x,y满足的可行域如图中阴影部分所示,图中A(1,0),B(2,1),C.当a≤0时,0≤y≤,1≤x≤2,所以1≤ax+y≤4不可能恒成立;当a>0时,借助图像得,当直线z=ax+y过点A时z取得最小值,当直线z=ax+y过点B或C时z取得最大值,故解得1≤a≤.故a∈.
E6 基本不等式
16.E6、E9[2014·辽宁卷] 对于c>0,当非零实数a,b满足4a2-2ab+4b2-c=0且使|2a+b|最大时,-+的最小值为________.
16.-2 [解析] 由题知2c=-(2a+b)2+3(4a2+3b2).
(4a2+3b2)≥(2a+b)2⇔4a2+3b2≥(2a+b)2,即2c≥(2a+b)2,
当且仅当=,即2a=3b=6λ(同号)时,
|2a+b|取得最大值,此时c=40λ2.
-+=-=-2≥-2,
当且仅当a=,b=,c=时,-+取最小值-2.
14.J3,E6[2014·山东卷] 若的展开式中x3项的系数为20,则a2+b2
的最小值为________.
14.2 [解析] Tr+1=C(ax2)6-r·=Ca6-r·brx12-3r,令12-3r=3,得r=3,所以Ca6-3b3=20,即a3b3=1,所以ab=1,所以a2+b2≥2ab=2,当且仅当a=b,且ab=1时,等号成立.故a2+b2的最小值是2.
10.E6,F7[2014·四川卷] 已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,·=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2 B.3 C. D.
10.B [解析] 由题意可知,F.设A(y,y1),B(y,y2),∴·=y1y2+yy=2,
解得y1y2=1或y1y2=-2.又因为A,B两点位于x轴两侧,所以y1y2<0,即y1y2=-2.
当y≠y时,AB所在直线方程为y-y1=(x-y)= (x-y),
令y=0,得x=-y1y2=2,即直线AB过定点C(2,0).
于是S△ABO+S△AFO=S△ACO+S△BCO+S△AFO=×2|y1|+×2|y2|+×|y1|=(9|y1|+8|y2|)≥×2=3,当且仅当9|y1|=8|y2|且y1y2=-2时,等号成立.当y=y时,取y1=,y2=-,则AB所在直线的方程为x=2,此时求得S△ABO+S△AFO=2××2×+××=,而>3,故选B.
14.E6,H4[2014·四川卷] 设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|PA|·|PB|的最大值是________.
14.5 [解析] 由题意可知,定点A(0,0),B(1,3),且两条直线互相垂直,则其交点P(x,y)落在以AB为直径的圆周上,
所以|PA|2+|PB|2=|AB|2=10.
∴|PA||PB|≤=5,
当且仅当|PA|=|PB|时等号成立.
E7 不等式的证明方法
20.M1 E7[2014·北京卷] 对于数对序列P:(a1,b1),(a2,b2),…,(an,bn),记
T1(P)=a1+b1,Tk(P)=bk+max{Tk-1(P),a1+a2+…+ak}(2≤k≤n),
其中max{Tk-1(P),a1+a2+…+ak}表示Tk-1(P)和a1+a2+…+ak两个数中最大的数.
(1)对于数对序列P:(2,5),(4,1),求T1(P),T2(P)的值;
(2)记m为a,b,c,d四个数中最小的数,对于由两个数对(a,b),(c,d)组成的数对序列P:(a,b),(c,d)和P′:(c,d),(a,b),试分别对m=a和m=d两种情况比较T2(P)和T2(P′)的大小;
(3)在由五个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P使T5(P)最小,并写出T5(P)的值.(只需写出结论)
20.解:(1)T1(P)=2+5=7,
T2(P)=1+max{T1(P),2+4}=1+max{7,6}=8.
(2)T2(P)=max{a+b+d,a+c+d},
T2(P′)=max{c+d+b,c+a+b}.
当m=a时,T2(P′)=max{c+d+b,c+a+b}=c+d+b.
因为a+b+d≤c+b+d,且a+c+d≤c+b+d,所以T2(P)≤T2(P′).
当m=d时,T2(P′)=max{c+d+b,c+a+b}=c+a+b.
因为a+b+d≤c+a+b,且a+c+d≤c+a+b,所以T2(P)≤T2(P′).
所以无论m=a还是m=d,T2(P)≤T2(P′)都成立.
(3)数对序列P:(4,6),(11,11),(16,11),(11,8),(5,2)的T5(P)值最小,
T1(P)=10,T2(P)=26,T3(P)=42,T4(P)=50,T5(P)=52.
19.A1、D3、E7[2014·天津卷] 已知q和n均为给定的大于1的自然数.设集合M={0,1,2,…,q-1},
集合A={x|x=x1+x2q+…+xnqn-1,xi∈M,i=1,2,…,n}.
(1)当q=2,n=3时,用列举法表示集合A.
(2)设s,t∈A,s=a1+a2q+…+anqn-1,t=b1+b2q+…+bnqn-1,其中ai,bi∈M,i=1,2,…,n.证明:若an1时,对x∈(0,a-1]有φ′(x)<0,
∴φ(x)在(0,a-1]上单调递减,
∴φ(a-1)<φ(0)=0.
即a>1时,存在x>0,使φ(x)<0,
故知ln(1+x)≥不恒成立.
综上可知,a的取值范围是(-∞,1].
(3)由题设知g(1)+g(2)+…+g(n)=++…+,
比较结果为g(1)+g(2)+…+g(n)>n-ln(n+1).
证明如下:
方法一:上述不等式等价于++…+,x>0.
令x=,n∈N+,则,x>0.
令x=,n∈N+,则ln>.
故有ln 2-ln 1>,
ln 3-ln 2>,
……
ln(n+1)-ln n>,
上述各式相加可得ln(n+1)>++…+,
结论得证.
方法三:如图,dx是由曲线y=,x=n及x轴所围成的曲边梯形的面积,而++…+是图中所示各矩形的面积和,
∴++…+>dx=
dx=n-ln(n+1),
结论得证.
E9 单元综合
16.E6、E9[2014·辽宁卷] 对于c>0,当非零实数a,b满足4a2-2ab+4b2-c=0且使|2a+b|最大时,-+的最小值为________.
16.-2 [解析] 由题知2c=-(2a+b)2+3(4a2+3b2).
(4a2+3b2)≥(2a+b)2⇔4a2+3b2≥(2a+b)2,即2c≥(2a+b)2,
当且仅当=,即2a=3b=6λ(同号)时,
|2a+b|取得最大值,此时c=40λ2.
-+=-=-2≥-2,
当且仅当a=,b=,c=时,-+取最小值-2.
12.B14、E9[2014·辽宁卷] 已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)-f(y)|<|x-y|.
若对所有x,y∈[0,1],|f(x)-f(y)|时,|f(x)-f(y)|=|f(x)-f(1)-(f(y)-f(0))|≤|f(x)-f(1)|+|f(y)-f(0)|<
|x-1|+|y-0|=-(x-y)+<.故kmin=.
3.[2014·天津卷] 设变量x,y满足约束条件则目标函数z=x+2y的最小值为( )
A.2 B.3 C.4 D.5
3.B [解析] 画出可行域,如图所示.解方程组得即点A(1,1).
当目标函数线过可行域内A点时,目标函数有最小值,即zmin=1×1+2×1=3.
16.[2014·广州七校联考] 不等式|x+2|+|x-1|≤5的解集为________.
16.[-3,2] [解析] 根据绝对值的几何意义,得不等式的解集为-3≤x≤2.
4.[2014·安徽六校联考] 若正实数x,y满足x+y=2,且≥M恒成立,则M的最大值为( )
A.1 B.2 C.3 D.4
4.A [解析] ∵x+y≥2,且x+y=2,∴2≥2,当且仅当x=y=1时,等号成立,∴xy≤1,∴≥1,∴1≥M,
∴Mmax=1.
7.[2014·福建宁德期末] 已知关于x的不等式x2-4ax+3a2<0(a>0)的解集为(x1,x2),则x1+x2+的最小值是( )
A. B. C. D.
7.C [解析] 由题知x1+x2=4a,x1x2=3a2,∴x1+x2+=4a+≥2 =,当且仅当a=时,等号成立.
6.[2014·长沙模拟] 若f(x)为奇函数,且在区间(0,+∞)上单调递增,f(2)=0,则>0的解集是( )
A.(-2,0)∪(0,2)
B.(-∞,-2)∪(0,2)
C.(-2,0)∪(2,+∞)
D.(-∞,-2)∪(2,+∞)
6.D [解析] 因为f(x)为奇函数,且在区间(0,+∞)上单调递增,所以f(x)在区间(-∞,0)上单调递增.又f(-x)=-f(x),所以>0等价于>0.
根据题设作出f(x)的大致图像如图所示.由图可知,>0的解集是(-∞,-2)∪(2,+∞).
13.[2014·浙江六市六校联考] 已知正数x,y满足x+y++=10,则x+y的最大值为________.
13.8 [解析] ∵+=10-(x+y),∴(x+y)+=10(x+y)-(x+y)2.又(x+y)+=10++≥10+6=16,∴10(x+y)-(x+y)2≥16,即(x+y)2-10(x+y)+16≤0,∴2≤x+y≤8,∴x+y的最大值为8.