四川省绵阳市江油中学2018-2019高二下学期期中考试数学（理）试卷

四川省绵阳市江油中学2018-2019高二下学期期中考试数学（理）试卷

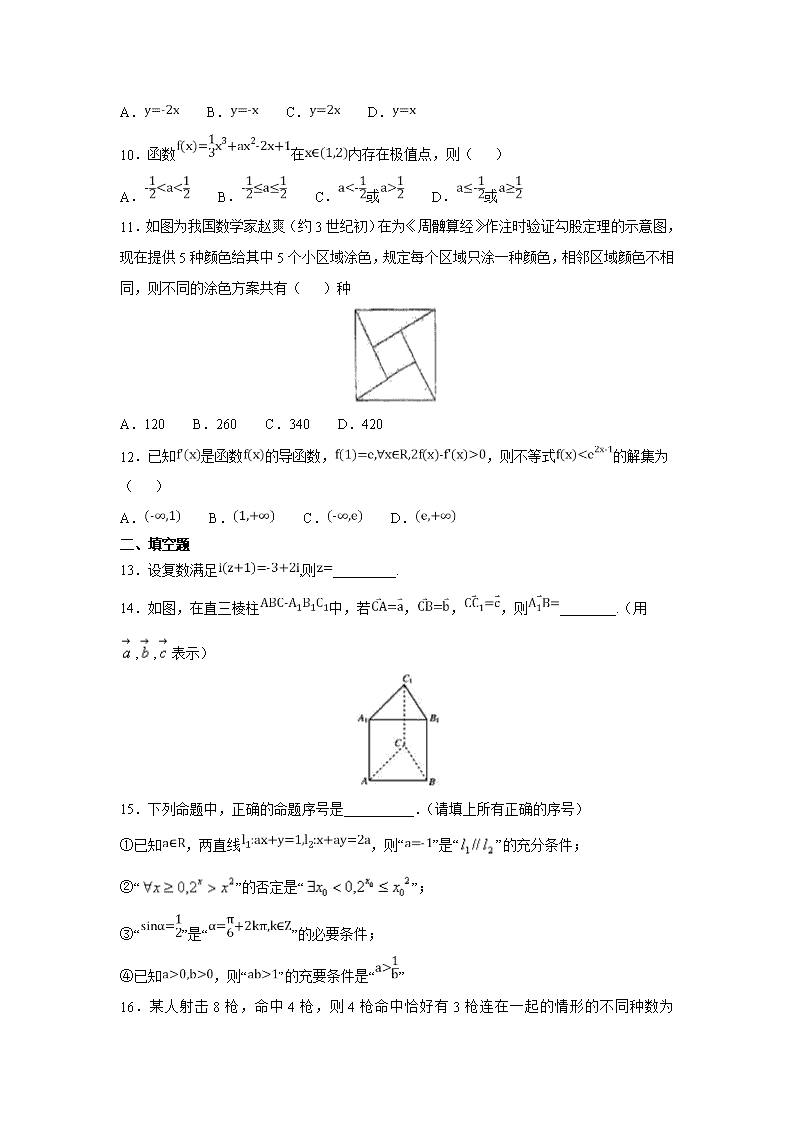
江油中学2018--2019学年度下期2017级半期考试 数学（理）试题 试卷命制：周琨翔 审核：王赟 一、单选题 ‎1．复数 (i为虚数单位)的共轭复数是(　　)‎ A．1+i B．1−i C．−1+i D．−1−i ‎2．已知，则“”是“”的(　　)‎ A．充分非必要条件 B．必要非充分条件 C．充要条件 D．既非充分又非必要条件 ‎3．设复数z满足(1+i)z=2i，则∣z∣=(　　)‎ A． B． C． D．2‎ ‎4．已知函数，则的值为(　　)‎ A． B．0 C． D．‎ ‎5．已知四棱锥中，平面ABCD的法向量为，，则点到底面的距离为（ ）‎ A． B． C．1 D．2‎ ‎6．命题“”的否定是（ ）‎ A． B． C． D．‎ ‎7．已知若,,三向量不能构成空间的一个基底，则实数的值为（ ）‎ A．0 B． C．9 D．‎ ‎8．已知集合，，现从这两个集合中各取出一个元素组成一个新的双元素组合，则可以组成这样的新集合的个数为(　　)‎ A． B． C． D．‎ ‎9．设函数．若为奇函数，则曲线在点处的切线方程为(　　)‎ A． B． C． D．‎ ‎10．函数在内存在极值点，则（ ）‎ A． B． C．或 D．或 ‎11．如图为我国数学家赵爽（约3世纪初）在为《周髀算经》作注时验证勾股定理的示意图，现在提供5种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同，则不同的涂色方案共有（ ）种 A．120 B．260 C．340 D．420‎ ‎12．已知是函数的导函数，，则不等式的解集为（ ）‎ A． B． C． D．‎ 二、填空题 ‎13．设复数满足,则_________.‎ ‎14．如图，在直三棱柱中，若，，，则________.（用,,表示）‎ ‎15．下列命题中，正确的命题序号是__________．（请填上所有正确的序号）‎ ‎①已知，两直线，则“”是“”的充分条件；‎ ‎②“”的否定是“”；‎ ‎③“”是“”的必要条件；‎ ‎④已知，则“”的充要条件是“”‎ ‎16．某人射击8枪，命中4枪，则4枪命中恰好有3枪连在一起的情形的不同种数为______.‎ 三、解答题 ‎17．已知，命题对任意，不等式恒成立；命题存在，使得成立．‎ ‎（）若为真命题，求的取值范围．‎ ‎（）当，若且为假，或为真，求的取值范围．‎ ‎18．已知函数 ‎(1)求曲线在点处的切线方程；‎ ‎(2)若函数恰有2个零点，求实数的取值范围.‎ ‎19．如图，已知多面体中，为菱形，，平面，，，.‎ ‎（1）求证：平面平面；‎ ‎（2）求二面角的余弦值.‎ ‎20．已知函数.‎ ‎(1)若函数在上为增函数，求的取值范围；‎ ‎(2)若函数有两个不同的极值点，记作,，且，证明： .‎ 参考答案 BACDD DDCDA DB ‎13．. 14． 15．①③④ 16．20‎ ‎17．（1）；（2）.‎ ‎（）若命题为真，则对任意，不等式恒成立，‎ 即当时，恒成立，‎ ‎∵当时，，∴，即，‎ 解得，即的取值范围是．‎ ‎（）当时，若命题为真，则存在，‎ 使得成立，即成立，故．‎ 若且为假命题，或为真命题，则，一真一假，‎ 若真假，则，得．‎ 若假真，则，得， ‎ 综上所述，的取值范围是．‎ ‎18．（1） （2）‎ ‎（1）因为，所以.‎ ‎ 所以 又 ‎ 所以曲线在点处的切线方程为 ‎ 即.（5分）‎ ‎（2）由题意得，，‎ ‎ 所以.‎ ‎ 由，解得，‎ ‎ 故当时，，在上单调递减；‎ ‎ 当时，，在上单调递增.‎ ‎ 所以.‎ ‎ 又，，‎ ‎ 结合函数的图象可得，若函数恰有两个零点，‎ ‎ 则解得.‎ ‎ 所以实数的取值范围为.‎ ‎19．(1)证明见解析；(2).‎ ‎（1）证明：∵，∴四点、、、共面.‎ 如图所示，连接，，相交于点，‎ ‎∵四边形是菱形，∴对角线，∵平面，‎ ‎∴，又，∴平面，∴，‎ 又，，∴平面，平面，‎ ‎∴平面平面.‎ ‎（2）取的中点，∵，，‎ ‎∴是等边三角形，∴，又，∴，‎ 以A点为坐标原点建立如图所示的空间直角坐标系，‎ 则，，，，.‎ ‎，，，.‎ ‎∵.∴，解得.‎ 设平面的法向量为，‎ 则，∴，‎ 取.‎ 同理可得：平面的法向量.‎ ‎∴.‎ 由图可知：二面角的平面角为钝角，‎ ‎∴二面角的余弦值为.‎ ‎20．（1） （2）见解析 解:（1）由题可知，函数的定义域为，‎ 因为函数在区间上为增函数，‎ 所以在区间上恒成立等价于，即，‎ 所以的取值范围是.‎ ‎（2）由题得，则 因为有两个极值点，‎ 所以 欲证等价于证，即，‎ 所以 因为，所以原不等式等价于.‎ 由可得，则‚.‎ 由‚可知，原不等式等价于，即 设，则，则上式等价于.‎ 令，则 因为，所以，所以在区间上单调递增，‎ 所以当时，，即，‎ 所以原不等式成立，即.‎