数学卷·2018届江西省九江一中高二上学期第一次月考数学试卷（理科） （解析版）

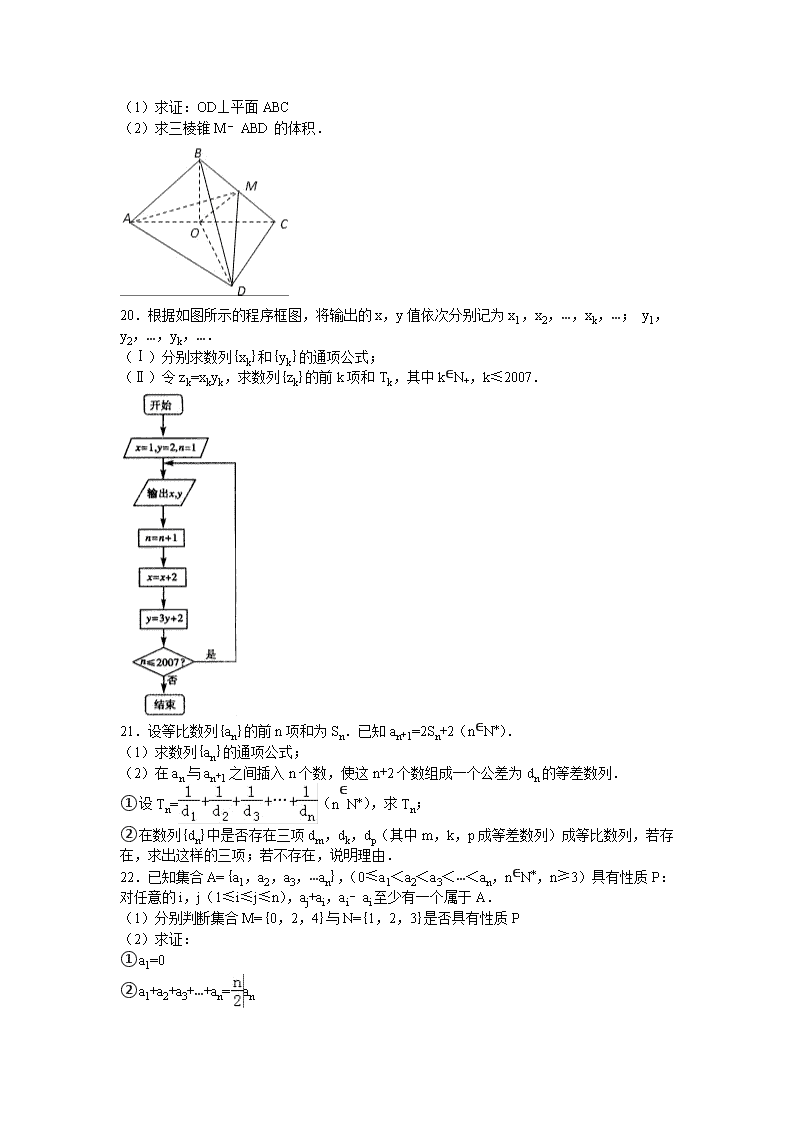
数学卷·2018届江西省九江一中高二上学期第一次月考数学试卷（理科） （解析版）

‎2016-2017学年江西省九江一中高二（上）第一次月考数学试卷（理科）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题列出的四个选项中，选出符合题目要求的一项.‎ ‎1．已知f（x）=，则f（f（3））的值为（　　）‎ A． B．0 C．1 D．3‎ ‎2．已知两条直线y=ax﹣2和3x﹣（a+2）y+1=0互相平行，则a等于（　　）‎ A．1或﹣3 B．﹣1或3 C．1或3 D．﹣1或﹣3‎ ‎3．等差数列{an}中，若a1+a4+a7=39，a3+a6+a9=27，则前9项的和S9等于（　　）‎ A．66 B．99 C．144 D．297‎ ‎4．设l是一条直线，α，β，γ是不同的平面，则在下列命题中，真命题的个数是（　　）个．‎ ‎①如果α⊥β，那么α内一定存在直线平行于β ‎②如果α不垂直于β，那么α内一定不存在直线垂直于β ‎③如果α⊥γ，β⊥γ，α∩β=l，那么l⊥γ A．0 B．1 C．2 D．3‎ ‎5．已知a=，b=20.3，c=0.30.2，则a，b，c三者的大小关系是（　　）‎ A．b＞c＞a B．b＞a＞c C．a＞b＞c D．c＞b＞a ‎6．下列关于公差d＞0的等差数列{an}的四个命题：‎ p1：数列{an}是递增数列；‎ p2：数列{nan}是递增数列；‎ p3：数列是递增数列；‎ p4：数列{an+3nd}是递增数列；‎ 其中真命题是（　　）‎ A．p1，p2 B．p3，p4 C．p2，p3 D．p1，p4‎ ‎7．已知等比数列{an}的前n项和为Sn=（x2+3x）2n﹣x+1，则a3的值为（　　）‎ A．﹣8 B．﹣4 C．1 D．不能确定 ‎8．在△ABC中，bsinA＜a＜b，则此三角形有（　　）‎ A．一解 B．两解 C．无解 D．不确定 ‎9．如图圆C内切于扇形AOB，∠AOB=，若在扇形AOB内任取一点，则该点在圆C内的概率为（　　）‎ A． B． C． D．‎ ‎10．设函数f（x）=sin（2x+），则下列结论正确的是（　　）‎ A．f（x）的图象关于直线x=对称 B．f（x）的图象关于点（，0）对称 C．f（x）的最小正周期为π，且在[0，]上为增函数 D．把f（x）的图象向右平移个单位，得到一个偶函数的图象 ‎11．已知等差数列{an}的前n项和为Sn，且=3，则a2016﹣a2014的值为（　　）‎ A．﹣3 B．0 C．6 D．12‎ ‎12．已知函数y=f（x）的定义域为R，当x＜0时，f（x）＞1，且对任意的实数x，y∈R，等式f（x）f（y）=f（x+y）恒成立．若数列{an}满足a1=f（0），且f（an+1）=，则a2010的值为（　　）‎ A．4016 B．4017 C．4018 D．4019‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分.把答案填在题中横线上.‎ ‎13．计算（lg2）2+lg2•lg50+lg25=　　．‎ ‎14．已知等比数列{an}为递增数列．若a1＞0，且2（an+an+2）=5an+1，则数列{an}的公比q=　　．‎ ‎15．圆x2+y2﹣2x+6y+5a=0关于直线y=x+2b成轴对称图形，则a﹣b的取值范围是　　．‎ ‎16．已知数列{an}（n=1，2，3，…，2016），圆C1：x2+y2﹣4x﹣4y=0，圆C2：x2+y2﹣2anx﹣2a2017﹣ny=0，若圆C2平分圆C1的周长，则数列{an}的所有项的和为　　．‎ ‎　‎ 三、解答题：本大题共6小题，共70分.解答应写出文字说明，演算步骤或证明过程.‎ ‎17．在公差不为0的等差数列{an}中，a3+a10=15，且a2，a5，a11成等比数列．‎ ‎（1）求{an}的通项公式；‎ ‎（2）设bn=，求数列{bn}的前n项和Sn．‎ ‎18．在△ABC中，a，b，c分别为角A，B，C所对的边，且4sin2﹣cos2A=．（参考公式：）‎ ‎（1）求角A的度数； ‎ ‎（2）若a=，b+c=3，求b和c的值．‎ ‎19．菱形ABCD的边长为3，AC与BD交于O，且∠BAD=60°．将菱形ABCD沿对角线AC折起得到三棱锥﹣ADC（如图），点M是棱C的中点，DM=．‎ ‎（1）求证：OD⊥平面ABC ‎（2）求三棱锥M﹣ABD的体积．‎ ‎20．根据如图所示的程序框图，将输出的x，y值依次分别记为x1，x2，…，xk，…； y1，y2，…，yk，…．‎ ‎（Ⅰ）分别求数列{xk}和{yk}的通项公式；‎ ‎（Ⅱ）令zk=xkyk，求数列{zk}的前k项和Tk，其中k∈N+，k≤2007．‎ ‎21．设等比数列{an}的前n项和为Sn．已知an+1=2Sn+2（n∈N*）．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）在an与an+1之间插入n个数，使这n+2个数组成一个公差为dn的等差数列．‎ ‎①设Tn=（n∈N*），求Tn；‎ ‎②在数列{dn}中是否存在三项dm，dk，dp（其中m，k，p成等差数列）成等比数列，若存在，求出这样的三项；若不存在，说明理由．‎ ‎22．已知集合A={a1，a2，a3，…an}，（0≤a1＜a2＜a3＜…＜an，n∈N*，n≥3）具有性质P：对任意的i，j（1≤i≤j≤n），aj+ai，ai﹣ai至少有一个属于A．‎ ‎（1）分别判断集合M={0，2，4}与N={1，2，3}是否具有性质P ‎（2）求证：‎ ‎①a1=0‎ ‎②a1+a2+a3+…+an=an ‎（3）当n=3或4时集合A中的数列{an}是否一定成等差数列？说明理由．‎ ‎　‎ ‎2016-2017学年江西省九江一中高二（上）第一次月考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题列出的四个选项中，选出符合题目要求的一项.‎ ‎1．已知f（x）=，则f（f（3））的值为（　　）‎ A． B．0 C．1 D．3‎ ‎【考点】对数的运算性质；函数的值．‎ ‎【分析】根据分段函数直接代入求值即可．‎ ‎【解答】解：由分段函数可知f（3）=log3（9﹣6）=log33=1，‎ ‎∴f（f（3））=f（1）=3•e1﹣1=3．‎ 故选D．‎ ‎　‎ ‎2．已知两条直线y=ax﹣2和3x﹣（a+2）y+1=0互相平行，则a等于（　　）‎ A．1或﹣3 B．﹣1或3 C．1或3 D．﹣1或﹣3‎ ‎【考点】两条直线平行的判定．‎ ‎【分析】应用平行关系的判定方法，直接求解即可．‎ ‎【解答】解：两条直线y=ax﹣2和3x﹣（a+2）y+1=0互相平行，‎ 所以 解得 a=﹣3，或a=1‎ 故选A．‎ ‎　‎ ‎3．等差数列{an}中，若a1+a4+a7=39，a3+a6+a9=27，则前9项的和S9等于（　　）‎ A．66 B．99 C．144 D．297‎ ‎【考点】等差数列的前n项和．‎ ‎【分析】根据等差数列的通项公式化简a1+a4+a7=39和a3+a6+a9=27，分别得到①和②，用②﹣①得到d的值，把d的值代入①即可求出a1，根据首项和公差即可求出前9项的和S9的值．‎ ‎【解答】解：由a1+a4+a7=3a1+9d=39，得a1+3d=13①，‎ 由a3+a6+a9=3a1+15d=27，得a1+5d=9②，‎ ‎②﹣①得d=﹣2，把d=﹣2代入①得到a1=19，‎ 则前9项的和S9=9×19+×（﹣2）=99．‎ 故选B．‎ ‎　‎ ‎4．设l是一条直线，α，β，γ是不同的平面，则在下列命题中，真命题的个数是（　　）个．‎ ‎①如果α⊥β，那么α内一定存在直线平行于β ‎②如果α不垂直于β，那么α内一定不存在直线垂直于β ‎③如果α⊥γ，β⊥γ，α∩β=l，那么l⊥γ A．0 B．1 C．2 D．3‎ ‎【考点】空间中直线与平面之间的位置关系．‎ ‎【分析】在①中，由面面垂直的性质得α内一定存在直线平行于β；在②中，由面面垂直的判定得α内一定不存在直线垂直于β；在③中，由线面垂直的判定定理得l⊥γ．‎ ‎【解答】解：由l是一条直线，α，β，γ是不同的平面，知：‎ 在①中，如果α⊥β，那么由面面垂直的性质得α内一定存在直线平行于β，故①正确；‎ 在②中，如果α不垂直于β，那么由面面垂直的判定得α内一定不存在直线垂直于β，故②正确；‎ 在③中，如果α⊥γ，β⊥γ，α∩β=l，那么由线面垂直的判定定理得l⊥γ，故③正确．‎ 故选：D．‎ ‎　‎ ‎5．已知a=，b=20.3，c=0.30.2，则a，b，c三者的大小关系是（　　）‎ A．b＞c＞a B．b＞a＞c C．a＞b＞c D．c＞b＞a ‎【考点】不等关系与不等式．‎ ‎【分析】利用指数函数的单调性即可判断出．‎ ‎【解答】解：∵，‎ ‎∴b＞c＞a．‎ 故选A．‎ ‎　‎ ‎6．下列关于公差d＞0的等差数列{an}的四个命题：‎ p1：数列{an}是递增数列；‎ p2：数列{nan}是递增数列；‎ p3：数列是递增数列；‎ p4：数列{an+3nd}是递增数列；‎ 其中真命题是（　　）‎ A．p1，p2 B．p3，p4 C．p2，p3 D．p1，p4‎ ‎【考点】等差数列的性质；命题的真假判断与应用．‎ ‎【分析】对于各个选项中的数列，计算第n+1项与第n项的差，看此差的符号，再根据递增数列的定义得出结论．‎ ‎【解答】解：∵对于公差d＞0的等差数列{an}，an+1﹣an=d＞0，∴命题p1：数列{an}是递增数列成立，是真命题．‎ 对于数列{nan}，第n+1项与第n项的差等于 （n+1）an+1﹣nan=（n+1）d+an，不一定是正实数，‎ 故p2不正确，是假命题．‎ 对于数列，第n+1项与第n项的差等于﹣==，不一定是正实数，‎ 故p3不正确，是假命题．‎ 对于数列{an+3nd}，第n+1项与第n项的差等于 an+1+3（n+1）d﹣an﹣3nd=4d＞0，‎ 故命题p4：数列{an+3nd}是递增数列成立，是真命题．‎ 故选D．‎ ‎　‎ ‎7．已知等比数列{an}的前n项和为Sn=（x2+3x）2n﹣x+1，则a3的值为（　　）‎ A．﹣8 B．﹣4 C．1 D．不能确定 ‎【考点】等比数列的前n项和．‎ ‎【分析】根据条件可以先得出，而由an=Sn﹣Sn﹣1即可得出等比数列{an}的首项，公比q=2，从而有2x2+5x+1=x2+3x，解出x，即可得出a1=﹣2，进而便可求出a3的值．‎ ‎【解答】解：根据题意，；‎ n≥2时，；‎ ‎∴等比数列{an}的首项a1=x2+3x，公比q=2；‎ ‎∴2x2+5x+1=x2+3x；‎ 解得x=﹣1；‎ ‎∴a1=﹣2；‎ ‎∴．‎ 故选：A．‎ ‎　‎ ‎8．在△ABC中，bsinA＜a＜b，则此三角形有（　　）‎ A．一解 B．两解 C．无解 D．不确定 ‎【考点】正弦定理．‎ ‎【分析】根据已知不等式得到A为锐角，且A小于B，利用正弦定理得到sinB小于1，可得出B为锐角或钝角，即三角形有两解．‎ ‎【解答】解：∵bsinA＜a＜b，‎ ‎∴sinA＜1，A＜B，‎ ‎∴0＜A＜90°，‎ 由正弦定理=得：asinB=bsinA＜a，即sinB＜1，‎ 当A＜B＜90°时，B为锐角；当90°＜B＜180°时，B为钝角，‎ 则此三角形有两解．‎ 故选：B ‎　‎ ‎9．如图圆C内切于扇形AOB，∠AOB=，若在扇形AOB内任取一点，则该点在圆C内的概率为（　　）‎ A． B． C． D．‎ ‎【考点】几何概型；扇形面积公式．‎ ‎【分析】本题是一个等可能事件的概率，试验发生包含的事件对应的包含的事件对应的是扇形AOB，满足条件的事件是圆，根据题意，构造直角三角形求得扇形的半径与圆的半径的关系，进而根据面积的求法求得扇形OAB的面积与⊙P的面积比．‎ ‎【解答】解：由题意知本题是一个等可能事件的概率，设圆C的半径为r，‎ 试验发生包含的事件对应的是扇形AOB，‎ 满足条件的事件是圆，其面积为⊙C的面积=π•r2，‎ 连接OC，延长交扇形于P．‎ 由于CE=r，∠BOP=，OC=2r，OP=3r，‎ 则S扇形AOB==；‎ ‎∴⊙C的面积与扇形OAB的面积比是．‎ ‎∴概率P=，‎ 故选C．‎ ‎　‎ ‎10．设函数f（x）=sin（2x+），则下列结论正确的是（　　）‎ A．f（x）的图象关于直线x=对称 B．f（x）的图象关于点（，0）对称 C．f（x）的最小正周期为π，且在[0，]上为增函数 D．把f（x）的图象向右平移个单位，得到一个偶函数的图象 ‎【考点】命题的真假判断与应用；函数y=Asin（ωx+φ）的图象变换．‎ ‎【分析】通过x=函数是否取得最值判断A的正误；通过x=，函数值是否为0，判断B的正误；利用函数的周期与单调性判断C的正误；利用函数的图象的平移判断D的正误．‎ ‎【解答】解：对于A，当x=时，函数f（x）=sin（2×+）=，不是函数的最值，判断A的错误；‎ 对于B，当x=，函数f（x）=sin（2×+）=1≠0，判断B的错误；‎ 对于C，f（x）的最小正周期为π，由，可得，k∈Z，在[0，]上为增函数，∴选项C的正确；‎ 对于D，把f（x）的图象向右平移个单位，得到函数f（x）=sin（2x+），函数不是偶函数，∴选项D不正确．‎ 故选：C．‎ ‎　‎ ‎11．已知等差数列{an}的前n项和为Sn，且=3，则a2016﹣a2014的值为（　　）‎ A．﹣3 B．0 C．6 D．12‎ ‎【考点】等差数列的前n项和．‎ ‎【分析】由等差数列{an}（公差为d）的前n项和为Sn，则=a1+（n﹣1），可得数列是等差数列，因此=3，进而得出．‎ ‎【解答】解：由等差数列{an}（公差为d）的前n项和为Sn，则=a1+（n﹣1），‎ ‎∴数列是等差数列，‎ ‎∴=3，d=6‎ 则a2016﹣a2014=2d=12．‎ 故选：D．‎ ‎　‎ ‎12．已知函数y=f（x）的定义域为R，当x＜0时，f（x）＞1，且对任意的实数x，y∈R，等式f（x）f（y）=f（x+y）恒成立．若数列{an}满足a1=f（0），且f（an+1）=，则a2010的值为（　　）‎ A．4016 B．4017 C．4018 D．4019‎ ‎【考点】数列与函数的综合．‎ ‎【分析】根据题意，底数小于1的指数函数符合题中条件，不妨令f（x）=，求得a1=f（0）=1，‎ 再由（n∈N*），得an+1=an+2，从而求得正确的结果．‎ ‎【解答】解：根据题意，不妨设f（x）=，（其中x∈R），‎ 则a1=f（0）=1；‎ ‎∵（n∈N*），‎ ‎∴==，‎ ‎∴an+1=an+2；‎ ‎∴数列{an}是以1为首项，以2为公差的等差数列；‎ ‎∴an=2n﹣1，‎ ‎∴a2010=4019．‎ 故选：D．‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分.把答案填在题中横线上.‎ ‎13．计算（lg2）2+lg2•lg50+lg25=　2　．‎ ‎【考点】对数的运算性质．‎ ‎【分析】将式子利用对数的运算性质变形，提取公因式，化简求值．‎ ‎【解答】解：原式=2 lg5+lg2•（1+lg5）+（lg2）2=2 lg5+lg2（1+lg5+lg2）‎ ‎=2 lg5+2 lg2=2；‎ 故答案为2．‎ ‎　‎ ‎14．已知等比数列{an}为递增数列．若a1＞0，且2（an+an+2）=5an+1，则数列{an}的公比q=　2　．‎ ‎【考点】等比数列的性质．‎ ‎【分析】由{an}为递增数列且a1＞0可知q＞1，由已知可得2（）=5anq，可求q ‎【解答】解：∵{an}为递增数列且a1＞0‎ ‎∴q＞1‎ ‎∵2（an+an+2）=5an+1，‎ ‎∴2（）=5anq ‎∴2+2q2=5q ‎∴q=2‎ 故答案为：2‎ ‎　‎ ‎15．圆x2+y2﹣2x+6y+5a=0关于直线y=x+2b成轴对称图形，则a﹣b的取值范围是　（﹣∞，4）　．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】由圆的方程求出圆心和半径，再根据圆心在直线y=x+2b上，求得a、b的值的范围，从而求得a﹣b的取值范围．‎ ‎【解答】解：由题意可得圆的方程为 （x﹣1）2+（y+3）2=10﹣5a，故圆心为（1，﹣3），半径为，‎ 由题意可得，圆心（1，﹣3）在直线y=x+2b上，∴﹣3=1+2b，且10﹣5a＞0，‎ ‎∴b=﹣2，a＜2，∴a﹣b＜4，‎ 故答案为：（﹣∞，4）．‎ ‎　‎ ‎16．已知数列{an}（n=1，2，3，…，2016），圆C1：x2+y2﹣4x﹣4y=0，圆C2：x2+y2﹣2anx﹣2a2017﹣ny=0，若圆C2平分圆C1的周长，则数列{an}的所有项的和为　4032　．‎ ‎【考点】数列与解析几何的综合；直线与圆的位置关系．‎ ‎【分析】根据两圆的关系求出两圆的公共弦，求出圆心C1的圆心，得到an+a2017﹣n=4即可求出{an}的所有项的和．‎ ‎【解答】解：设圆C1与圆C2交于A，B，则直线AB的方程为：‎ x2+y2﹣4x﹣4y﹣（x2+y2﹣2anx﹣2a2017﹣ny）=0，‎ 化简得：（an﹣2）x+（a2017﹣n﹣2）y=0，‎ ‎∵圆C1：x2+y2﹣4x﹣4y=0的标准方程为圆（x﹣2）2+（y﹣2）2=8，‎ ‎∴圆心C1：（2，2）．‎ 又圆C2平分圆C1的周长，‎ 则直线AB过C1：（2，2）．，‎ 代入AB的方程得：2（an﹣2）+2（a2017﹣n﹣2）=0，‎ 即an+a2017﹣n=4，‎ ‎∴{an}的所有项的和为a1+a2+…+a2017=（a1+a2016）+（a2+a2015）+…+（a1008+a1009）=1008×4=4032．‎ 故答案为：4032．‎ ‎　‎ 三、解答题：本大题共6小题，共70分.解答应写出文字说明，演算步骤或证明过程.‎ ‎17．在公差不为0的等差数列{an}中，a3+a10=15，且a2，a5，a11成等比数列．‎ ‎（1）求{an}的通项公式；‎ ‎（2）设bn=，求数列{bn}的前n项和Sn．‎ ‎【考点】数列的求和．‎ ‎【分析】（1）设等差数列的公差为d，并由条件确定d的范围，根据等差数列的通项公式及等比数列的性质、以及题意列出关于首项和公差的方程组，求出公差和首项后代入等差数列的通项公式化简即可；‎ ‎（2）把（1）求出的an代入bn，再求出bn的表达式，然后由裂项相消法来求数列{bn}的前n项和Sn．‎ ‎【解答】解：（1）设正项等差数列{an}的公差为d，则d≠0，‎ 由a3+a10=15，且a2，a5，a11成等比数列得，‎ ‎，‎ ‎②化为6d2﹣3da1=0，‎ 因为d≠0，‎ 所以a1=2d，代入①解得，‎ d=1，则a1=2，‎ 所以，an=a1+（n﹣1）•d=n+1；‎ ‎（2）由（1）知，an=n+1，则 bn===﹣，‎ 所以Sn=﹣+﹣+﹣+…+﹣=﹣=，‎ 即Sn=．‎ ‎　‎ ‎18．在△ABC中，a，b，c分别为角A，B，C所对的边，且4sin2﹣cos2A=．（参考公式：）‎ ‎（1）求角A的度数； ‎ ‎（2）若a=，b+c=3，求b和c的值．‎ ‎【考点】余弦定理；三角函数中的恒等变换应用．‎ ‎【分析】（1）已知等式利用二倍角的正弦、余弦函数公式化简，再利用诱导公式变形，求出cosA的值，即可确定出A的度数；‎ ‎（2）利用余弦定理表示出cosA，再利用完全平方公式变形，将a，b+c及cosA的值代入求出bc的值，与b+c的值联立即可求出b与c的值．‎ ‎【解答】解：（1）由题设得2[1﹣cos（B+C）]﹣（2cos2A﹣1）=，‎ ‎∵cos（B+C）=﹣cosA，‎ ‎∴2（1+cosA）﹣2cos2A+1=，‎ 整理得（2cosA﹣1）2=0，‎ ‎∴cosA=，‎ ‎∴A=60°；‎ ‎（2）∵cosA=====，‎ ‎∴bc=2，‎ 又∵b+c=3，‎ ‎∴b=1，c=2或b=2，c=1．‎ ‎　‎ ‎19．菱形ABCD的边长为3，AC与BD交于O，且∠BAD=60°．将菱形ABCD沿对角线AC折起得到三棱锥﹣ADC（如图），点M是棱C的中点，DM=．‎ ‎（1）求证：OD⊥平面ABC ‎（2）求三棱锥M﹣ABD的体积．‎ ‎【考点】棱柱、棱锥、棱台的体积；直线与平面垂直的判定．‎ ‎【分析】（1）先证明OD⊥OM，OD⊥AC，结合OM∩AC=O，由线面垂直的判定得OD⊥平面ABC；‎ ‎（2）判断OD为三棱锥D﹣ABC的高，求出△ABM，然后求解三棱锥的体积．‎ ‎【解答】（Ⅰ）证明：由题意，OM=OD=，‎ ‎∵DM=，‎ ‎∴∠DOM=90°，OD⊥OM．‎ 又∵ABCD是菱形，∴OD⊥AC．‎ ‎∵OM∩AC=O，‎ ‎∴OD⊥平面ABC；‎ ‎（2）解：三棱锥M﹣ABD的体积等于三棱锥D﹣ABM的体积．‎ 由（1）知，OD⊥平面ABC，‎ ‎∴OD=为三棱锥D﹣ABM的高．‎ ‎△ABM的面积为×3××=，‎ ‎∴所求体积等于××=．‎ ‎　‎ ‎20．根据如图所示的程序框图，将输出的x，y值依次分别记为x1，x2，…，xk，…； y1，y2，…，yk，…．‎ ‎（Ⅰ）分别求数列{xk}和{yk}的通项公式；‎ ‎（Ⅱ）令zk=xkyk，求数列{zk}的前k项和Tk，其中k∈N+，k≤2007．‎ ‎【考点】程序框图；等差数列的通项公式；等比数列的通项公式；数列的求和．‎ ‎【分析】（I）根据框图可知数列{xk}为等差数列，首项为1，公差为2，进而根据等差数列的通项公式求得数列{xk}的通项公式，对于{yk}易得yk+1=3yk+2变形得yk+1+1=3（yk+1），利用等比数列的通项公式求得yk+1=3k进一步求出yk=3k﹣1．‎ ‎（II）根据（I）中求得的{xk}和{yk}的通项公式，求得zk=（2k﹣1）3k﹣（2k﹣1），进而利用错位相减法求得答案．‎ ‎【解答】解：（I）依框图得数列{xk}为等差数列，首项为1，公差为2‎ 所以xk=1+2×（k﹣1）=2k﹣1‎ 而对于{yk}易得yk+1=3yk+2变形得yk+1+1=3（yk+1）‎ 所以{yk+1}是以y1+1=3为首项，以3为公比的等比数列，‎ 所以yk+1=3k 所以yk=3k﹣1‎ ‎（II）由题意知，zk=（2k﹣1）（3k﹣1）=（2k﹣1）3k﹣（2k﹣1）‎ 设Sk=1×3+3×32+5×33+…+（2k﹣1）•3k ‎3Sk=1×32+3×33+…+（2k﹣3）•3k+（2k﹣1）3k+1‎ 两式相减得 ‎﹣2Sk=2（1﹣k）•3k+1﹣6‎ 所以Dk=3﹣（1﹣k）•3k+1．‎ ‎∴Tk=3﹣（1﹣k）•3k+1﹣k2．‎ ‎　‎ ‎21．设等比数列{an}的前n项和为Sn．已知an+1=2Sn+2（n∈N*）．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）在an与an+1之间插入n个数，使这n+2个数组成一个公差为dn的等差数列．‎ ‎①设Tn=（n∈N*），求Tn；‎ ‎②在数列{dn}中是否存在三项dm，dk，dp（其中m，k，p成等差数列）成等比数列，若存在，求出这样的三项；若不存在，说明理由．‎ ‎【考点】数列递推式；等差数列与等比数列的综合．‎ ‎【分析】（1）设等比数列{an}的公比为q，若q=1，则an=a1，an+1=a1，Sn=na1，这与an+1=2Sn+2矛盾，故q≠1，由an+1=2Sn+2得，由此能够推导出an=2×3n﹣1．‎ ‎（2）由an=2×3n﹣1，知an+1=2×3n，因为an=an+（n+1）dn，所以．‎ ‎（i）=，由错位相减法能够得到．‎ ‎（ii）假设在数列{dn}中存在dm，dk，dp（其中m，k，p成等差数列）成等比数列，则dk2=dmdp，由m，k，p成等差数列，知m+p=2k，由此可得m=k=p这与题设矛盾，所以在数列{dn}中不存在三项dm，dk，dp（其中m，k，p成等差数列）成等比数列．‎ ‎【解答】解：（1）设等比数列{an}的公比为q，若q=1，则an=a1，an+1=a1，Sn=na1，这与an+1=2Sn+2矛盾，‎ 故q≠1，由an+1=2Sn+2得，…‎ 故取，解得，故an=2×3n﹣1…‎ ‎（2）由（1），知an=2×3n﹣1，an+1=2×3n 因为an+1=an+（n+1）dn，所以…‎ ‎（i）=，‎ 则…‎ 所以 ‎=‎ 所以…‎ ‎（ii）假设在数列{dn}中存在dm，dk，dp（其中m，k，p成等差数列）成等比数列 则dk2=dmdp，即 因为m，k，p成等差数列，所以m+p=2k①‎ 上式可以化简为k2=mp②由①②可得m=k=p这与题设矛盾 所以在数列{dn}中不存在三项dm，dk，dp（其中m，k，p成等差数列）成等比数列…‎ ‎　‎ ‎22．已知集合A={a1，a2，a3，…an}，（0≤a1＜a2＜a3＜…＜an，n∈N*，n≥3）具有性质P：对任意的i，j（1≤i≤j≤n），aj+ai，ai﹣ai至少有一个属于A．‎ ‎（1）分别判断集合M={0，2，4}与N={1，2，3}是否具有性质P ‎（2）求证：‎ ‎①a1=0‎ ‎②a1+a2+a3+…+an=an ‎（3）当n=3或4时集合A中的数列{an}是否一定成等差数列？说明理由．‎ ‎【考点】元素与集合关系的判断．‎ ‎【分析】（1）利用新定义，可以判断集合M={0，2，4}具有性质P，N={1，2，3}不具有性质P；‎ ‎（2）根据数列：a1，a2，…an（0≤a1＜a2…＜an），n≥3时具有性质P，对任意i，j（1≤i＜j≤n），aj+ai与aj﹣ai两数中至少有一个是该数列中的一项 ‎（3）确定a1=0，再利用新定义，即可判断具有性质P的集合A中的数列{an}是否一定成等差数列．‎ ‎【解答】（1）解：集合M={0，2，4}具有性质P，N={1，2，3}不具有性质P．‎ ‎∵集合M={0，2，4}中，aj+ai与aj﹣ai（1≤i≤j≤2）两数中都是该数列中的项，4﹣2是该数列中的项，‎ ‎∴集合M={0，2，4}具有性质P；‎ N={1，2，3}中，3在此集合中，则由题意得3+3和3﹣3至少一个一定在，而3+3=6不在，所以3﹣3=0一定是这个集合的元素，而此集合没有0，故不具有性质P；‎ ‎（2）①数列中的最大项an，显然an+an=2an不是数列中的项，则必有an﹣an=0属于该数列，故0∈A，所以a1=0，‎ ‎②若数列A具有该性质P，设an是最大项，则具有性质ai+an（1＜i≤n，i∈N*），不在A中，则an﹣ai是数列A中的项，则依题意：an﹣an＜an﹣an﹣1＜an﹣an﹣2＜…＜an﹣a2＜an﹣a1，则由给的数列A的性质可知；an﹣an=a1，an﹣an﹣1=a2，an﹣an﹣2=a3，…an﹣a2=an﹣1，an﹣a1=an，将前面n个式子相加得：nan﹣（a1+a2+a3+…an﹣1+an）=a1+a2+a3+…+an﹣1+an，故nan=2（a1+a2+a3+…an﹣1+an），‎ 故a1+a2+a3+…+an=an ‎（3）解：n=3时，∵数列a1，a2，a3具有性质P，0≤a1＜a2＜a3‎ ‎∴a2+a3与a3﹣a2至少有一个是该数列中的一项，‎ ‎∵a1=0，a2+a3不是该数列的项，∴a3﹣a2=a2，∴a1+a3=2a2，数列{an}一定成等差数列；‎ n=4时，∵数列a1，a2，a3，a4具有性质P，0≤a1＜a2＜a3＜a4，‎ ‎∴a3+a4与a4﹣a3至少有一个是该数列中的一项，‎ ‎∵a3+a4不是该数列的项，∴a4﹣a3=a2，或a4﹣a3=a3，‎ 若a4﹣a3=a2，则数列{an}一定成等差数列；若a4﹣a3=a3，则数列{an}不一定成等差数列；‎