2018-2019学年山东省泰安第一中学高一10月学情检测数学试题（解析版）

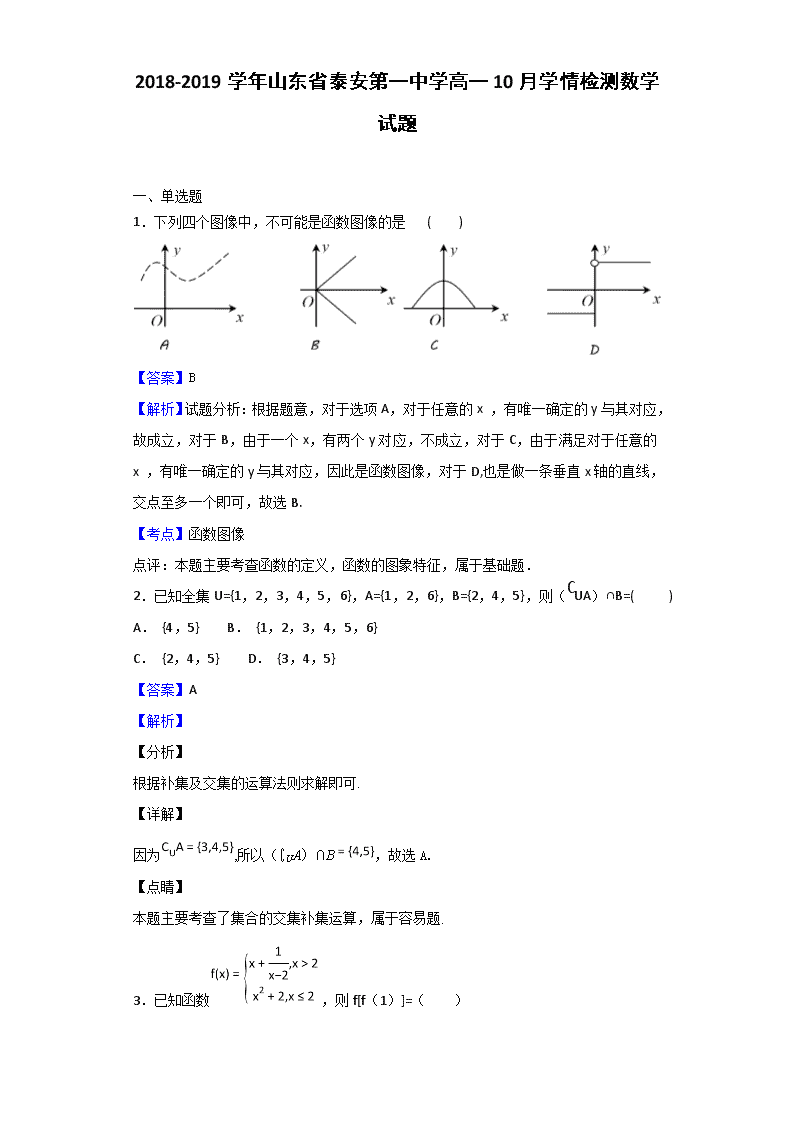
2018-2019学年山东省泰安第一中学高一10月学情检测数学试题（解析版）

‎2018-2019学年山东省泰安第一中学高一10月学情检测数学试题 一、单选题 ‎1．下列四个图像中，不可能是函数图像的是 ( )‎ ‎【答案】B ‎【解析】试题分析：根据题意，对于选项A，对于任意的x ，有唯一确定的y与其对应，故成立，对于B，由于一个x，有两个y对应，不成立，对于C，由于满足对于任意的x ，有唯一确定的y与其对应，因此是函数图像，对于D,也是做一条垂直x轴的直线，交点至多一个即可，故选B.‎ ‎【考点】函数图像 点评：本题主要考查函数的定义，函数的图象特征，属于基础题．‎ ‎2．已知全集U={1，2，3，4，5，6}，A={1，2，6}，B={2，4，5}，则（∁UA）∩B=( )‎ A． {4，5} B． {1，2，3，4，5，6}‎ C． {2，4，5} D． {3，4，5}‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据补集及交集的运算法则求解即可.‎ ‎【详解】‎ 因为,所以（∁UA）∩B，故选A.‎ ‎【点睛】‎ 本题主要考查了集合的交集补集运算，属于容易题.‎ ‎3．已知函数，则f[f（1）]=（　　）‎ A． B． 2 C． 4 D． 11‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据分段函数的解析式，先计算，再计算.‎ ‎【详解】‎ 因为，所以，又 所以，故，选C.‎ ‎【点睛】‎ 本题主要考查了分段函数求函数值 ，属于中档题.‎ ‎4．已知集合A={x∈N|x﹣3＜0}，则满足条件B⊆A的集合B的个数为（　　）‎ A． 2 B． 3 C． 4 D． 8‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据集合的描述法可知，集合A中的元素为 ，所以A的子集个数为.‎ ‎【详解】‎ 由解得，又，所以，故, 因为B⊆A，所以B是A的子集，故B可以是，故选C.‎ ‎【点睛】‎ 本题主要考查了集合的描述法表示，集合的子集，属于中档题.‎ ‎5．下列有关集合的写法正确的是（ ）‎ A． B． C． D． ‎ ‎【答案】D ‎【解析】试题分析：元素和集合是属于或不属于的关系，空集是没有元素的集合，所以D选项正确．‎ ‎【考点】元素和集合的关系．‎ ‎6．函数，当时是增函数，当时是减函数，则等于（ ）‎ A． -3 B． 13 C． 7 D． 5‎ ‎【答案】B ‎【解析】试题分析：由题意知函数的对称轴，所以，所以，故选B．‎ ‎【考点】函数的单调性．‎ ‎7．函数f（x）=的定义域为（　　）‎ A． [3，+∞） B． [3，4）∪（4，+∞） C． （3，+∞） D． [3，4）‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 要使函数有意义，只需函数各个部分都有意义，即，解得,写出定义域即可.‎ ‎【详解】‎ 要使函数有意义，则，解得，故选B.‎ ‎【点睛】‎ 本题主要考查了函数的定义域，属于中档题.‎ ‎8．若函数f（x）对于任意实数x恒有f（x）﹣2f（﹣x）=3x﹣1，则f（x）等于（　　）‎ A． x+1 B． x﹣1 C． 2x+1 D． 3x+3‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据题意，可得，与已知方程联立方程组，把视作未知数，即可求解.‎ ‎【详解】‎ 因为，所以，联立方程组，解得，故选A.‎ ‎【点睛】‎ 本题主要考查了函数解析式的求法，属于中档题.‎ ‎9．函数f（x）=|x2﹣6x+8|的单调递增区间为（　　）‎ A． [3，+∞） B． （﹣∞，2），（4，+∞）‎ C． （2，3），（4，+∞） D． （﹣∞，2]，[3，4]‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 画出的图象，将图象在x轴下方的部分对称到x轴上方，即可得到的图象，根据图象可写出函数的单调递增区间.‎ ‎【详解】‎ 画出的图象如图：‎ 由图象可知，函数的增区间为，故选C.‎ ‎【点睛】‎ 本题主要考查了函数的调性，函数的图象，属于中档题.‎ ‎10．已知函数f（x）=在R上单调递增，则实数a的取值范围是（　　）‎ A． [﹣1，+∞） B． （﹣1，+∞） C． [﹣1，0） D． （﹣1，0）‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据分段函数的单调性，函数在R上单调递增，需要每段都单调递增且左段的右端点函数值不大于右段的左端点的函数值，即可求出a的取值范围.‎ ‎【详解】‎ 因为函数在R上是递增函数，所以，解得，故选C.‎ ‎【点睛】‎ 本题主要考查了分段函数的单调性，属于中档题.‎ ‎11．设＝{1，2，3，4，5} ，若＝{2}，，，则下列结论正确的是（ ）‎ A． 且 B． 且 C． 且 D． 且 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据题意画出韦恩图，确定出A与B,即可作出判断.‎ ‎【详解】‎ 因为＝{1，2，3，4，5} ，若＝{2}，，，所以画出韦恩图：‎ ‎ ，，则且，故选B.‎ ‎【点睛】‎ 本题主要考查了集合的交、并、补集的混合运算，集合的韦恩图，属于中档题.‎ ‎12．已知不等式ax2+5x+b＞0的解集是{x|2＜x＜3}，则不等式bx2﹣5x+a＞0的解集是（　　）‎ A． {x|x＜﹣3或x＞﹣2} B． {x|x＜﹣或x＞﹣}‎ C． {x|﹣＜x＜﹣} D． {x|﹣3＜x＜﹣2}‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由题意可知，的根为，利用根与系数的关系可求出，即可解出不等式的解.‎ ‎【详解】‎ 由题意可知，的根为, ,解得，，不等式bx2﹣5x+a＞0可化为，即，解得，故选C.‎ ‎【点睛】‎ 本题主要考查了一元二次不等式的解法，一元二次不等式与一元二次函数的关系，属于中档题.‎ 二、填空题 ‎13．若集合A={x|ax2+ax+1=0，x∈R}不含有任何元素，则实数a的取值范围是_____．‎ ‎【答案】0≤a＜4‎ ‎【解析】‎ ‎【分析】‎ 当时，显然方程无解，当时，利用判别式小于0即可求解.‎ ‎【详解】‎ 当时,原方程可化为，显然无解，当时，一元二次方程无解则需，即，解得，综上.‎ ‎【点睛】‎ 本题主要考查了集合，一元二次方程，分类讨论，属于中档题.‎ ‎14．设函数，若，则实数a的取值范围是________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据题意，当时，解，当时，解，即可求出.‎ ‎【详解】‎ 当时,由得，解得，又，所以无解，当时，由得，解得，故填.‎ ‎【点睛】‎ 本题主要考查了分段函数，解不等式及分类讨论的思想，属于中档题.‎ ‎15．.若集合，，则集合_________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由 ，化简集合B ,然后求交集即可.‎ ‎【详解】‎ 因为，所以，即，所以，故填.‎ ‎【点睛】‎ 本题主要考查了集合的化简，集合的交集运算，属于中档题.‎ ‎16．关于x的不等式mx2﹣2x+1≥0，对任意的x∈（0，3]恒成立，则m的取值范围是________．‎ ‎【答案】[1，+∞）‎ ‎【解析】‎ ‎【分析】‎ 当时，不等式可化为，对任意的x∈（0，3]不恒成立，当时，分离参数可得对任意的x∈（0，3]恒成立，令 ，求其最大值即可求解.‎ ‎【详解】‎ ‎(1) 当时，不等式可化为，对任意的x∈（0，3]不恒成立,‎ ‎(2) 当时,原不等式可化为对任意的x∈（0，3]恒成立，令 ，当，即时，，所以，综上.‎ ‎【点睛】‎ 本题主要考查了不等式的恒成立，二次函数的最值，属于中档题.‎ 三、解答题 ‎17．（10分）若集合A={x|x2+5x﹣6=0}，B={x|x2+2（m+1）x+m2﹣3=0}．‎ ‎（1）若m=0，写出A∪B的子集；‎ ‎（2）若A∩B=B，求实数m的取值范围．‎ ‎【答案】（1）A∪B的子集：Φ，{﹣6}，{﹣3}，{1}，{﹣6，﹣3}，{﹣6，1}，{﹣3，1}，{﹣6，﹣3，1}‎ ‎（2）m的取值范围是（﹣∞，﹣2]．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由x2+5x﹣6=0得,所以，当时，化简,求出A∪B，写出子集即可（2）由知,分类讨论即可.‎ ‎【详解】‎ ‎（1）根据题意，‎ m=0时，B={1，﹣3}，A∪B={﹣6，﹣3，1}；‎ ‎∴A∪B的子集：Φ，{﹣6}，{﹣3}，{1}，{﹣6，﹣3}，{﹣6，1}，{﹣3，1}，{﹣6，﹣3，1}，‎ ‎（2）由已知B⊆A，‎ ‎m＜﹣2时，B=Φ，成立 ‎‚m=﹣2时，B={1}⊆A，成立 ‎ƒm＞﹣2时，若B⊆A，则B={﹣6，1}；‎ ‎∴⇒m无解，‎ 综上所述：m的取值范围是（﹣∞，﹣2]．‎ ‎【点睛】‎ 本题主要考查了集合的并集运算，子集的概念，分类讨论的思想，属于中档题.‎ ‎18．（12分）已知函数．‎ ‎（1）判断函数在区间上的单调性，并用定义证明你的结论；‎ ‎（2）求该函数在区间上的最大值与最小值．‎ ‎【答案】（1）见解析 （2）函数的最大值为，最小值为 ‎【解析】‎ ‎【分析】‎ ‎（1）函数是增函数，利用定义证明即可（2）根据函数是增函数，当x取最小值时，函数有最小值，x取最大值时，函数有最大值.‎ ‎【详解】‎ ‎（1）函数在上是增函数．‎ 证明：任取，且，‎ 则．‎ 易知，，所以，即，‎ 所以函数在上是增函数．‎ ‎（2）由（1）知函数在上是增函数，‎ 则函数的最大值为，最小值为 ‎【点睛】‎ 本题主要考查了函数单调性的定义法证明以及函数单调性的运用，属于中档题.‎ ‎19．已知函数.‎ ‎（1）做出函数图象；‎ ‎（2）说明函数的单调区间（不需要证明）；‎ ‎（3）若函数的图象与函数的图象有四个交点，求实数的取值范围.‎ ‎【答案】（1）见解析；（2）见解析；（3）‎ ‎【解析】‎ ‎【分析】‎ ‎(1)分段画出函数图像即可；（2）根据图像直接由定义得到函数的单调区间；（3）根据图象易得：使得y=m和有4个交点即可.‎ ‎【详解】‎ ‎（1）如图： ‎ ‎（2）函数的单调递增区间为；单调递减区间为. ‎ ‎（3）根据图象易得：使得y=m和有4个交点即可.故 ‎【点睛】‎ 这个题目考查了分段函数的奇偶性，和分段函数单调区间的求法，以及函数有几个交点求参的问题；分段函数的单调区间是指各段的单调区间，值域需要将各段并到一起，定义域将各段的定义域并到一起.‎ ‎20．（12分）设集合A={x|x+1≤0或x﹣4≥0}，B={x|2a≤x≤a+2}‎ ‎（1）若A∩B=B，求实数a的取值范围．‎ ‎（2）若A∩B≠∅，求实数a的取值范围．‎ ‎【答案】（1）a≥2或a≤﹣3；（2）a=2或a≤﹣．‎ ‎【解析】试题分析：（1）若，共包含两种情况，一是为空集，—是不为空集，但与无公共元素，由此我们可以构造关于的不等式组，解不等式组即可得到实数的取值范围；（2）若，则可分为三种情况，一是为空集，二是满足中，三是满足中；构造关于的不等式组，解不等式组即可到实数的取值范围.‎ 试题解析：（1）或或，综上所述：结论为或.‎ ‎（2），有三种情况：①；②；③，综上，的取值范围为或，故答案为（1）或；（2）或.‎ ‎【方法点睛】本题主要考查集合的基本运算、分类讨论思想.属于难题.分类讨论思想解决高中数学问题的一种重要思想方法，是中学数学四种重要的数学思想之一，尤其在解决含参数问题发挥着奇特功效，大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透，这样才能快速找准突破点. 充分利用分类讨论思想方法能够使问题条理清晰，进而顺利解答，希望同学们能够熟练掌握并应用与解题当中.‎ ‎21．已知二次函数f（x）的图象过点（0，4），对任意x满足f（3﹣x）=f（x），且f（1）=2．‎ ‎（1）若f（x）在（a，2a﹣1）上单调递减，求实数a的取值范围．‎ ‎（2）设函数h（x）=f（x）﹣（2t﹣3）x，其中t∈R，求h（x）在区间[0，1]上的最小值g （t）．‎ ‎【答案】（1）a∈（1，]；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由知，函数的对称轴为 ，函数在 上单调，只需即可求解 （2）化简函数，根据二次函数的对称轴，分 三种情况讨论，即可求出最小值.‎ ‎【详解】‎ ‎（1）设f（x）=ax2+bx+c（a＞0），由于过点（0，4），‎ ‎∴c=4．‎ 由f（3﹣x）=f（x）得，a（3﹣x）2+b（3﹣x）+4=ax2+bx+4，即3a+b=0①‎ 又f（1）=a+b+4=2‎ ‎∴a=1，b=﹣3，‎ 故f（x）=x2﹣3x+4，‎ 则函数的单调递减区间为：（﹣∞，]‎ 若f（x）在（a，2a﹣1）上单调递减，‎ 则a＜2a﹣1≤‎ 解得：a∈（1，]；‎ ‎（2）函数h（x）=f（x）﹣（2t﹣3）x=x2﹣2tx+4的图象是开口朝上，且以直线x=t为对称轴的抛物线，‎ 当t≤0时，h（x）在区间[0，1]上为增函数，当x=0时，h（x）取最小值，即g （t）=h（0）=4．‎ 当0＜t＜1时，h（x）在区间[0，t]上为减函数，区间[t，1]上为增函数，当x=t时，h（x）取最小值，即g （t）=h（t）=4﹣t2．‎ 当t≥1时，h（x）在区间[0，1]上为减函数，当x=1时，h（x）取最小值，即g （t）=h（1）=5﹣2t．‎ ‎【点睛】‎ 本题主要考查了二次函数的单调性，二次函数在给定区间上的最值，分类讨论的思想，属于难题.‎ ‎22．（12分）已知函数f(x)对任意的实数m，n都有：f(m＋n)＝f(m)＋f(n)－1，‎ 且当x＞0时，有f(x)＞1.‎ ‎(1)求f(0)．‎ ‎(2)求证：f(x)在R上为增函数．‎ ‎(3)若f(1)＝2，且关于x的不等式f(ax－2)＋f(x－x2)＜3对任意的x∈[1，＋∞)恒成立，求实数a的取值范围．‎ ‎【答案】(1) f(0)＝1 (2)见解析 (3) (－∞，2－1)‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用赋值法，令，可得．（2）根据函数单调性的定义并结合所给的函数的性质可证明结论成立．（3）根据题意可将不等式化为，再由函数f(x)在R上为增函数可得x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立，然后根据二次函数在所给区间上的最值的求法求出函数的最小值后可得所求．‎ ‎【详解】‎ ‎(1)解令m=n=0,则f(0)=2f(0)-1,‎ ‎∴f(0)=1.‎ ‎(2)证明：设x1,x2∈R,且x1f(x1)．‎ 故f(x)在R上为增函数．‎ ‎(3)解∵，‎ 即，‎ ‎∴，‎ ‎∵f(1)=2,‎ ‎∴.‎ 又f(x)在R上为增函数,‎ ‎∴．‎ ‎∴对任意的x∈[1,+∞)恒成立.‎ 令，‎ ‎①当≤1,即a≤1时,函数在[1,+∞)上单调递增，‎ 由,得a<3,‎ ‎∴a≤1；‎ ‎②当>1,即a>1时,由,得，‎ ‎∴‎ 综上可得实数a的取值范围为．‎ ‎【点睛】‎ ‎（1）解决抽象函数问题的两个原则：一是要合理运用赋值法解题，合理选取变量的取值达到求解的目的；二是要灵活运用所给的函数的性质．‎ ‎（2）解决函数中的恒成立问题时，可转化为求函数的最值的问题处理．在本题中求二次函数的最值时要注意抛物线的开口方向和对称轴与区间的关系，对于含有字母的问题要注意分类讨论．‎