2014宁德1月份质检理数试卷

2014宁德1月份质检理数试卷

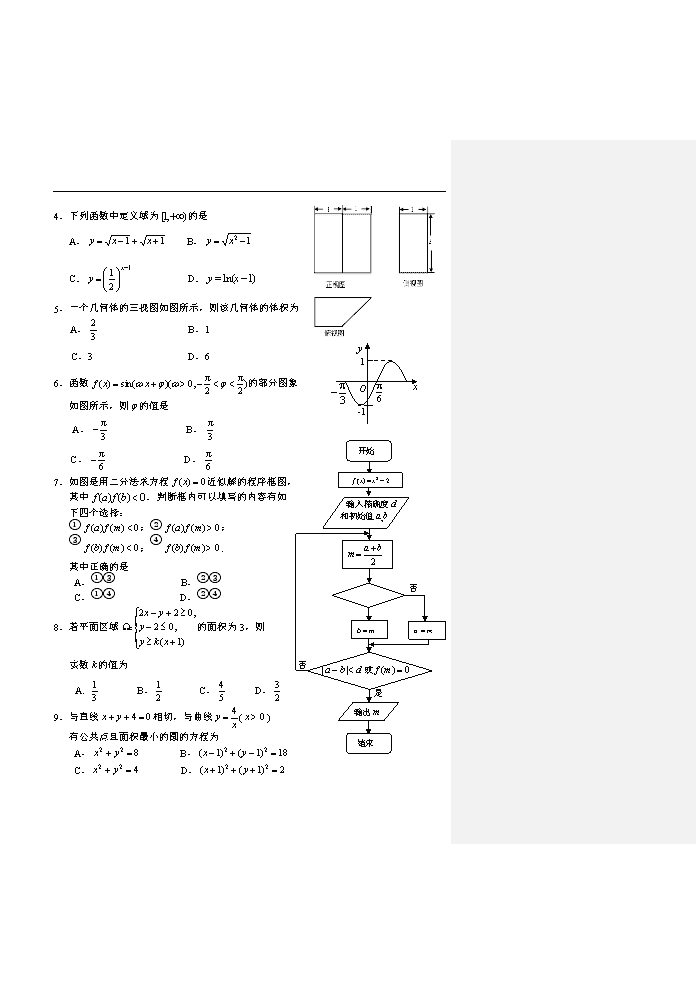
‎2014年宁德市普通高中毕业班单科质量检查 数学（理科）试卷 本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分．本卷满分150分，考试时间120分钟．‎ 注意事项:‎ ‎1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．‎ ‎2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．‎ ‎3．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚．‎ ‎4．保持答题卡卡面清楚，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．‎ 参考公式：‎ ‎ ‎锥体体积公式 柱体体积公式 其中为底面面积，为高 球的表面积公式 体积公式 其中为球的半径 第I卷（选择题 共50分）‎ 一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．集合,,若,则的值为 A. 0 B. ‎1 C. D. 0或1‎ ‎2. 命题：“，”，则为 A. ， B．，‎ C．， D．，‎ ‎3. 直线在平面内，直线在平面内，下列命题正确的是 A． B．‎ C． D．‎ 4． 下列函数中定义域为的是 ‎ A． B．‎ ‎ C． D．‎ ‎5．一个几何体的三视图如图所示，则该几何体的体积为 A． B．1 ‎ ‎1‎ C．3 D．6‎ O 6． 函数的部分图象 ‎-1‎ ‎ 如图所示，则的值是 开始 ‎ 输入精确度 和初始值a,b 否 或 是 否 输出m 结束 ‎ A． B． ‎ C． D．‎ 7． 如图是用二分法求方程近似解的程序框图，‎ ‎ 其中．判断框内可以填写的内容有如 ‎ 下四个选择：‎ ‎ ①；②；‎ ‎ ③；④.‎ ‎ 其中正确的是 A． ‎①③ B．②③‎ ‎ C．①④ D．②④‎ ‎8．若平面区域的面积为3，则 ‎ 实数的值为 A. B． C． D．‎ ‎9．与直线相切，与曲线()‎ ‎ 有公共点且面积最小的圆的方程为 A． ‎ B．‎ C． D．‎ ‎10. 给定有限单调递增数列（至少有两项），其中，定义集合 ‎．若对任意的点，存在点使得（O为坐标原点），则称数列具有性质P．例如数列：具有性质P．以下对于数列的判断：‎ ‎ ①数列：，，1，3具有性质P；‎ ‎ ②若数列满足 则该数列具有性质P；‎ ‎ ③若数列具有性质P，则数列中一定存在两项，使得；‎ ‎ 其中正确的是 ‎ A.①②③ B.②③ C. ①② D.③‎ 第II卷 （非选择题共100分）‎ 二、填空题：本大题共5小题，每小题4分，共20分．把答案填在答题卡相应位置．‎ ‎11. 已知向量，，若，共线，则实数的值为 . ‎ ‎12. 已知复数，为虚数单位为实数，则 .‎ ‎13．锐角三角形中，分别为角所对的边．若，， ‎ ‎ ，则= .‎ 14. 若函数且，且的图象关于轴对称，则 ‎ ‎ 的最小值为__________.‎ ‎15. 已知，过点作一直线与双曲线相交且仅有一个公共点，则该直线的倾斜角恰好等于此双曲线渐近线的倾斜角或；类比此思想，已知，过点作一直线与函数的图象相交且仅有一个公共点，则该直线的倾斜角为 . ‎ ‎（背面还有试题）‎ 三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．‎ ‎16．(本小题满分13分)‎ ‎ 已知数列的前项和为，且满足．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）记，求数列的前项和．‎ ‎17．(本小题满分13分)‎ ‎ 已知是定义在上的奇函数，且当时, .‎ ‎ (Ⅰ)求当时，的表达式；‎ ‎ (Ⅱ)求满足不等式的的取值范围.‎ ‎18．(本小题满分13分)‎ 已知函数)．‎ ‎（Ⅰ）求函数的单调递增区间及对称轴方程；‎ ‎（Ⅱ）当时，的最大值为9，求实数的值．‎ A B 北 ‎19． (本小题满分13分)‎ 为了监测某海域的船舶航行情况，海事部门在该海域设立了如图所示东西走向，相距海里的，两个观测站，观测范围是到，两观测站距离之和不超过海里的区域.‎ ‎（Ⅰ）建立适当的平面直角坐标系，求观测区域边界曲线的方程； ‎ ‎（Ⅱ）某日上午7时，观测站B发现在其正东‎10海里的C处，有一艘轮船正以每小时8海里的速度向北偏西45°方向航行，问该轮船大约在什么时间离开观测区域？‎ ‎(参考数据：)‎ ‎20． (本小题满分14分)‎ ‎ 如图已知圆锥的底面半径为4，母线长为8，三角形是圆锥的一个轴截面, ‎ B O S A P θ B1‎ D 是上的一点，且．动点从点出发沿着圆锥的侧面运动到达点，当其运动路程最短时在侧面留下的曲线如图所示．将轴截面绕着轴逆时针旋转后，母线与曲线相交于点． ‎ ‎ （Ⅰ）若，证明：平面平面；‎ ‎ （Ⅱ）若，求二面角的余弦值．‎ ‎21．(本小题满分14分)‎ 已知函数，若曲线在点处的切线平行于轴．‎ ‎ (Ⅰ) 求实数的值；‎ ‎（Ⅱ）函数恰有两个零点．‎ ‎ （i）求函数的单调区间及实数的取值范围；‎ ‎ （ii）求证：．‎ ‎2014年宁德市普通高中毕业班单科质量检查 数学（理科）试题参考答案及评分标准 说明：‎ ‎ 一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解法不同，可根据试题的主要考查内容比照评分标准指定相应的评分细则．‎ ‎ 二、对计算题，当考生的解答在某一部分解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．‎ ‎ 三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．‎ ‎ 四、只给整数分数，选择题和填空题不给中间分．‎ 一、选择题：本题考查基础知识和基本运算，每小题5分，满分50分．‎ ‎1．B 2．D 3．D 4．A 5．C 6．A 7．C 8．B 9．A 10．D 二、填空题：本题考查基础知识和基本运算，每小题4分，满分20分．‎ ‎11．3 12． 13． 14．8 15．或 ‎（附题10解答：对于①，取时，若存在满足，得，即，数列中不存在这样的项，因此不具有性质P．‎ 对于②，取时，不存在，使得，故②不具有性质P．‎ 对于③，取，若数列具有性质P，则存在点使得，‎ 即，又，所以，故③正确）‎ 三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程和演算步骤．‎ ‎16．本题考查数列等基本知识，考查推理论证能力和运算求解能力，考查函数与方程的思想、化归与转化的思想，满分13分．‎ 解：（Ⅰ）因为令，解得．…………………………………2分 因为 所以[来…………………………3分 两式相减得，…………………………………………………5分 所以是首项为1，公比为2的等比数列，……………………………6分 所以．…………………………………………………7分 ‎（Ⅱ）解：，[来,科，网ZXXK] …………………………8分 ‎ ‎ ‎ …………………10分 ‎…………………………………………………13分 ‎（说明：等比求和正确得2分，等差求和正确得1分）‎ ‎17．本小题主要考查函数、不等式等基础知识，考查推理论证能力、运算求解能力，考查函数与方程的思想、化归与转化的思想，满分13分．‎ 解：(Ⅰ)当时，，，…………………………………2分 又为奇函数,‎ ‎，…………………………………4分 即．…………………………5分 又，即，……………6分 故当时，．……………7分 ‎(Ⅱ)由(Ⅰ)知，在上是增函数，…………………………9分 ‎，………………10分 即………………11分 解得.………………………13分 ‎18．本小题主要考查三角函数的图象与性质、三角恒等变换等基础知识，考查推理论证能力和运算求解能力，考查函数与方程的思想、化归与转化的思想和数形结合的思想，满分13分．‎ 解（Ⅰ）‎ ‎ ………………………3分每使用一个公式，正确得1分，不同解法相应给分.‎ ‎ ‎ ‎ ………………………5分 由，………………………6分 得．‎ ‎∴函数的单调增区间为．………………………7分 由得，‎ ‎∴函数的对称轴方程是.………………………8分 ‎（Ⅱ）∵当时，，………………………9分 ‎ ∴ ，………………………11分 ‎ ∴，……………………12分 ‎ ∴，解得．‎ ‎∴实数的值为5.…………………………………………13分 ‎（由得出的最大值为1，得2分；正确推出的最大值为，再得1分；正确求出m的值得1分）‎ ‎19．本题主要考查直线、椭圆、直线与椭圆的位置关系等基础知识，考查运算求解能力、‎ 推理论证能力，考查函数与方程思想、化归与转化思想，考查应用意识，满分13分．‎ 解：以所在直线为轴，线段的垂直平分线为轴建立平面直角坐标系．……1分 ‎（Ⅰ）依题意可知：考察区域边界曲线是以A,B为焦点的椭圆，…………2分 B 北 O y C D 设椭圆方程为：，‎ 则，……………………5分每个等式各1分 解得，……………………6分 ‎∴考察区域边界曲线的方程为：.………………………………7分 ‎（不同的建系方式，对照上面的给分点相应评分）‎ ‎（Ⅱ）设轮船在观测区域内航行的时间为小时，航线与区域边界的交点为、，‎ ‎∵，，‎ ‎∴直线方程：…………………………………………………8分 ‎ 联立方程，整理得：，…………………9分 ‎ 解得………………………………………………………………10分 ‎ ∴……………………………………………11分 ‎∴ （小时）. ……………………………………………12分 ‎∴轮船大约在当日上午10时离开观测区域. . ……………………………13分 ‎（其他解法相应给分）‎ ‎20．本小题主要考查直线与平面的位置关系，二面角的大小等基础知识，考查空间想象能力、推理论证能力和运算求解能力，考查化归与转化思想、数形结合思想，满分14分．‎ 解法一：（Ⅰ）证明：∵，‎ A1‎ O A 是 θ B1‎ D ‎ ∴．…………………………………1分 ‎∵,∴ ……………2分 又∵，∴平面，…4分 又∵平面，‎ ‎∴平面平面，……………………6分 又∵平面，‎ A z A1‎ B O θ B1‎ A1‎ D S x y Q 图（1）‎ ‎∴平面平面．………………………………7分 ‎（Ⅱ）以为原点，AB所在直线为x轴，线段AB的中垂线为y轴，‎ OS所在直线为z轴建立如图（1）所示的空间直角坐标系，…………8分 则，，‎ 将圆锥半侧面图展开，如图（2）所示，‎ 由已知可求． ……………………9分 又，．‎ A S B D P B1‎ 图（2）‎ ‎，．‎ ‎，在中，．‎ ‎∴点为的中点．……………………10分 如图（1）面，面面 过作交于，则面，‎ ‎．……………………11分 ‎，． ‎ 设平面的法向量为，则 解得：……………………12分 取平面的法向量为……………………13分 所求的二面角的余弦值为.……………………14分 S x A D B Q S B P C A A1‎ 解法二：（I）同解法一；‎ ‎（Ⅱ）与解法一同,得：，．…………11分 过作交于，连结，‎ ‎∵, , 又∵‎ ‎，.‎ 则为二面角的平面角. ……………13分 中，，‎ 所求的二面角的余弦值为．…………………………………………14分 ‎（其它解法相应给分）‎ ‎21．本小题主要考查函数、函数与导数等基础知识，考查推理论证能力，运算求解能力，考查函数与方程的思想，数形结合的思想，化归与转化思想，满分14分．‎ 解法一：（Ⅰ）由，且，………………………………2分 ‎ 解得．…………………………………………3分 ‎（Ⅱ）（i），.‎ ‎ 令 ,…………………………………………4分 当即时，，‎ 所以在上单调递减，‎ 此时只存在一个零点，不合题意；………………………………………5分 当时，令，解得.‎ 当变化时，和变化情况如下表：‎ 极小值 ‎…………………………………………6分 由题意可知，.‎ 设，‎ 当时，即，此时恰有一个零点，不合题意；…………… 7分 当且时，，………………………………8分 当时，，当时，‎ 所以在上单调递增，在上单调递减，‎ 所以，此时恰有两个零点．‎ 综上，的取值范围是.…………………………………………9分 ‎（ii）证明：函数有两个零点，‎ ‎，‎ 两式相减得，‎ ‎．…………………………………………10分 要证，‎ 只要证，只要证，‎ 只要证，……………………………11分 只要证．…………………………………………12分 设，则，‎ 在（1，+∞）上单调递增，………………………………13分 ‎，‎ ‎ ．…………………………………………14分 解法二：（I），（II）（i）同解法一．‎ ‎（ii）显然，故是函数的一个零点，不妨设．…………………10分 由是函数的另一个零点，‎ 所以，即.……………………………11分 又，…………………12分 设，且，‎ ‎，，‎ 所以在上单调递减，在上单调递增，‎ 故，…………………………………………13分 所以的单调递增区间为和．‎ 又，‎ 当时，，当时，,‎ 所以，即.…………………14分 ‎（其它解法相应给分）‎ y 图（2）‎ D Q