湖北省钟祥一中2012届高三五月适应性考试（三）

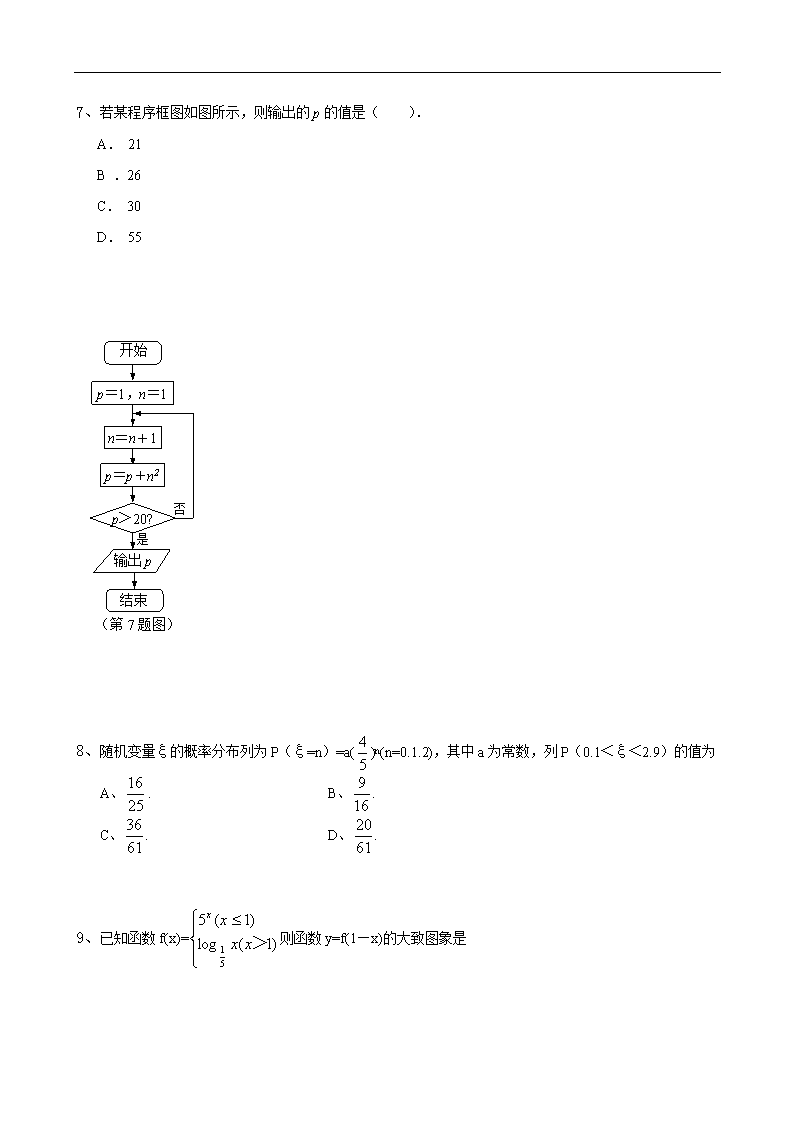
湖北省钟祥一中2012届高三五月适应性考试（三）

湖北省钟祥一中2012届高三五月适应性考试（三）‎ 一、选择题 ‎1、在直三棱柱A1 B‎1 ‎C1—ABC中，BAC=，｜AB｜=｜AC｜=｜CC1｜=1.已知G、E分别为A1 B1和CC1的中点，D与F分别为线段AC和AB上的动点（不含端点），若GD⊥EF，则线段DF的长度的取值范围是 ‎ A、. B、 C、 D.、‎ ‎2、设（2x+）4=ao+a1x+a2x2+a3x3+a4x4.则（ao+a2+a4）2—（a1+a3）2=‎ ‎ A、2. B、—2. C、1. D、—1‎ ‎3、将直线x+y+1=0绕点（—1，0）逆时针旋转90°后，再沿y轴正方向向上平移1个单位，此时直线恰与圆x2+(y—1)2=r2相切，则圆的半径r的值为 ‎ A、. B、. C、 D、1.‎ ‎4、在数列｛an｝中，an+1=，若a1=，则a2012的值为 ‎ A、. B、. C、 D、‎ ‎5、关于x的函数f(x)=sin(φx+φ)有以下命题：‎ ‎ ①、φ，f(x+2π)=f(x)； ②、，f(x+1)=f(x)‎ ‎ ③、φ，f(x)都不是偶函数 ④、，使f(x)为奇函数 ‎ 其中假命题的序号是：‎ ‎ A、①③. B、①④. C、②④. D、②③.‎ ‎6、若向量与的夹角为120°，且｜｜=1，｜｜=2， =+，则有 ‎ A、. B、. C、∥. D、∥ ‎ ‎7、若某程序框图如图所示，则输出的p的值是（ ）．‎ ‎ A． 21 ‎ ‎ B ．‎26 ‎‎ ‎ 　‎ ‎ C． 30 ‎ ‎ D． 55‎ 开始 p＝1，n＝1‎ n＝n＋1‎ p＞20?‎ 输出p 结束 ‎（第7题图）‎ 是 否 p＝p＋n2‎ ‎8、随机变量ξ的概率分布列为P（ξ=n）=a()n(n=‎0.1.2‎)，其中a为常数，列P（0.1＜ξ＜2.9）的值为 ‎ A、. B、 ‎ ‎ C、 D、‎ ‎9、已知函数f(x)=则函数y=f(1—x)的大致图象是 ‎10、集合M=函数y=有意义，N=x｜｜x+1｜＞2则MN ‎ A、（—1，3）. B、（1，2） C、（—1，2） D、R 二、填空题 ‎11、已知xi＞0(i=1，2，3，…10.)，且xi=1. 则T=的最小值为 　 ‎ ‎12、已知函数f(x)=log2x,正项等比数列｛bn｝的公比为2，若f(b12.b14….b20)=4.则2=　　　　　‎ ‎13、已知椭圆（a＞b＞0）的左右焦点分别为F1,F2，P是椭圆上一点。PF‎1F2为以F2P为底边的等腰三角形，当60°＜PF‎1F2120°，则该椭圆的离心率的取值范围是　　　　‎ ‎（二）选考题（请考生在第15、16两题中任选一题作答，请先在答题卡指定位置将你所选的题目序号后的方框用2B铅笔涂黑. 如果全选，则按第15题作答结果计分.）‎ ‎14、 如图，是圆的切线，是切点，直线交圆于、两点，是的中点，连结并延长交圆于点，若，∠，则________．‎ ‎15、 在直角坐标系xoy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为cos (θ－)=1，曲线C2的方程为.（θ为参数，θ[o,2π））,a,b为实常数，当点（a,b）与曲线C1上点间的最小距离为时，则C1与C2交点间的距离为 ‎ ‎16、设复数z满足（其中i为虚数单位）则｜z｜= ‎ 三、解答题 ‎17、已知数列｛an｝是以d为公差的等差数列，数列｛bn｝是以q为公比的等比数列 ‎（Ⅰ）若数列｛bn｝的前n项和为Sn，且a1＝b1＝d＝2，S3＜5b2＋a88－180，求整数q的值 ‎（Ⅱ）在（Ⅰ）的条件下，试问数列｛bn｝中是否存在一项bk，使得b,k恰好可以表示为该数列中连续P（P∈N，P≥2）项和？请说明理由。‎ ‎（Ⅲ）若b1＝ar，b2＝as≠ar， b3=at（其中t＞s＞r，且（s—r）是（t—r）的约数）求证：数列｛bn｝中每一项都是数列｛an｝中的项.‎ ‎18、‎ 设ABC的内角A、B、C的对边分别为a、b、c，cos(A—C)+cos B=，b2=ac，求B.‎ ‎19、‎ 盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球. 规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得－1分 . 现从盒内任取3个球 ‎（Ⅰ）求取出的3个球中至少有一个红球的概率；‎ ‎（Ⅱ）求取出的3个球得分之和恰为1分的概率；‎ ‎（Ⅲ）设为取出的3个球中白色球的个数，求的分布列和数学期望.‎ ‎20、‎ 如图所示， 四棱锥P－ABCD的底面是边长为1的正方形，PA^CD，PA = 1， PD＝，E为PD上一点，PE = 2ED．‎ ‎（Ⅰ）求证：PA ^平面ABCD；‎ ‎（Ⅱ）求二面角D－AC－E的余弦值；‎ ‎（Ⅲ）在侧棱PC上是否存在一点F，使得BF // 平面AEC？若存在，指出F点的位置，并证明；若不存在，说明理由．‎ ‎21、 已知函数y=f(x)在定义域（—1+∞）内满足f(o)=0，且f／(x)=，(f／(x))是f(x)的导数）‎ ‎（Ⅰ）求f(x)的表达式.‎ ‎（Ⅱ）当a=1时，讨论f(x)的单调性 ‎（Ⅲ）设h(x)=（ex—P）2＋（x－P）2，证明：h(x)≥‎ ‎22、 已知圆G：x2+y2—2x—，经过椭圆（a＞b＞0）的右焦点F及上顶点B，过椭圆外一点M（m,0）(m＞0)的倾斜角为的直线l交椭圆于C、D两点.‎ ‎（Ⅰ）求椭圆方程 ‎（Ⅱ）当右焦点在以线段CD为直径的圆E的内部，求实数m的范围 以下是答案 一、选择题 ‎1、 A ‎ ‎2、 C ‎3、 A ‎4、 C ‎5、 A ‎6、 A ‎7、 C ‎8、 C ‎9、 D ‎10、 B 二、填空题 ‎11、100 ‎ ‎12、8 ‎ ‎13、（） ‎ ‎14、 ‎ ‎15、4‎ ‎16、 ‎ 三、解答题 ‎17、（Ⅰ）由题意知an=2n，bn=2·n—1 由S3＜5b2＋a88－180得.‎ ‎ b1+b2+b3＜a88＋5b2－180 b1—4b2+b3＜176—180q2—4q+3＜0‎ ‎ 解得1＜q＜3,q为值数.q=2. ‎ ‎（Ⅱ）假设数列｛bn｝中存在一项bk满足bk=bm+bm+1+……bm+p—1‎ ‎ bn=2n bk＞bm+p—12k＞‎2m+p—1k＞m+p—1k≥m+p.]‎ ‎ 又bk=2k=bm+bm+1=‎2m+‎2m+1+‎2m+p—1==‎2m+p—‎‎2m ‎ 2k＜‎2m+pk＜m+p与k≥m+p矛盾，不存在 ‎（Ⅲ）由b1=ar得b2=b1q=arq=as=ar+(s—r)d，则d=‎ ‎ 又b3=b1q2=ar.q2=at=ar+(t—r)darq2—ar=(t—r)‎ ‎ ar(q+1)(q—1)=ar(q—1).‎ ‎ as≠arb1≠b2 q≠1.又ar≠0‎ ‎ 故q=—1又t＞s＞r且（s—r）是(t—r)的约数 q是正整数且q≥2‎ 对于数列｛bn｝中任一项bi(这里只讨论i＞3的情形)，‎ 有bi=arqi—1= ar+ar(qi—1—1)= ar+ ar（q—1）（1+q+…+qi—2）‎ ‎= ar+d(s—r)(1+q+…+qi—2)=ar＋[((s—r)(1+q+…+qi+2)+1)—1]d 由于（s—r）(1+q+…+qi—2)+1为正整数 bi一定是数列｛an｝中的项 ‎ ‎ ‎18、由cos(A－C)＋cosB＝及B＝π－（A＋C）得 cos(A－C)－cos(A＋C)＝‎ cosAcosC＋sinAsinC－cosAcosC＋sinAsinC＝‎ sinAsinC＝‎ 又由b2＝ac及止弦定理得sin2B＝sinAsinC 故sin2B＝‎ ‎∴sinB＝或sinB＝－（舍去）‎ 于是B＝或B＝‎ 又由b2＝ac知b≤a或b≤c ∴B＝‎ ‎19、‎ ‎（Ⅰ） ‎ ‎（Ⅱ）记 “取出1个红色球，2个白色球”为事件，“取出2个红色球， 1个黑色球”为事件，则 . ‎ ‎（Ⅲ）可能的取值为. ‎ ‎， ，‎ ‎， . ‎ 的分布列为:‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ 的数学期望 ‎ ‎20、‎ 解：（Ⅰ） PA = PD = 1 ,PD = 2 , ‎ ‎ PA2 + AD2 = PD2, 即：PA ^ AD ‎ ‎ 又PA ^ CD , AD , CD 相交于点D, ‎ ‎ PA ^ 平面ABCD ‎ ‎（Ⅱ）过E作EG//PA 交AD于G，‎ 从而EG ^ 平面ABCD，‎ 且AG = 2GD , EG = PA = , ‎ 连接BD交AC于O, 过G作GH//OD ，交AC于H，‎ 连接EH．GH ^ AC , EH ^ AC , ‎ Ð EHG为二面角D—AC―E的平面角． ‎ tanÐEHG = = ．二面角D—AC―E的平面角的余弦值为 ‎（Ⅲ）以AB , AD , PA为x轴、y轴、z轴建立空间直角坐标系．‎ 则A（0 ，0， 0），B（1，0，0） ，C（1，1，0），P（0，0，1），E（0 , ,）, = （1,1,0）, ‎ ‎ = （0 , , ） ‎ 设平面AEC的法向量= （x, y,z） , 则 ‎ ，即：， 令y = 1 , ‎ 则 = （- 1,1, - 2 ） ‎ 假设侧棱PC上存在一点F, 且＝ ， ‎ ‎（0 £ £ 1）, 使得：BF//平面AEC, 则× ＝ 0．‎ 又因为：＝ + ＝ （0 ，1，0）+ （-,-,）= （-,1-,）,‎ × ＝+ 1- - 2 = 0 , = ,‎ 所以存在PC的中点F, 使得BF//平面AEC． ‎ ‎21、（Ⅰ）由f／(x)＝.可得f(x)=ln(1+x)—ax+b，b为实常数.又f(0)＝0b＝0.‎ f(x)＝ln(1+x)—ax.‎ ‎（Ⅱ）当a=1时，f(x)= ln(1+x)—x. (x＞－1)‎ f／(x)＝　　　∵x＞－1‎ ‎ 由f／(x)＝0x＝0 ∴当x∈（－1，0]时f／(x)≥0，此时f(x)递增 当x∈（0，＋∞）时，f／(x)＜０，此时f(x)递减 即f(x)在（－1，0）上单调增，在（0，＋∞）上单调减 ‎（Ⅲ）由（Ⅱ）知f(x)≤f(0)＝0在（－1，＋∞）内恒成立 ‎∴ln (1＋x) ≤x ‎∴ex≥1＋x ex－x≥1 ∴（ex－x）2≥1‎ ‎∴≤≤（ex－P）2＋（P－x）2‎ 即h(x)＝（ex－P）2＋（P－x）2≥‎ ‎22、（Ⅰ）∵圆G经过点F、B　　∴F（2，0），B（0，）‎ ‎∴椭圆的焦半径c＝2，短半轴长b＝　　　∴a2＝b2＋o2＝6‎ 故椭圆方程为 ‎（Ⅱ）设直线l的方程为y＝－　（m＞）‎ 由 2x2－2mx＋(m2－6)＝0‎ 由△＝4m2－8（m2－6）＞0　　m2＜12 ‎ ‎∴－2＜m＜2‎ 又m＞ ∴＜m＜2‎ 设C(x1，y1)，D(x2，y2)，则x1＋x2＝m，x1x2＝‎ ‎∴y1·y2＝［－］［－］＝‎ ‎∵　　‎ ‎＝（x1－2）（x2－2）＋y1y2‎ ‎＝x1x2－＋＋4‎ ‎＝‎ ‎∵点F在圆E内部 ∴＜0‎ 即＜0 0＜m＜3‎ 又∵＜m＜2‎ ‎∴实数m的取值范围为（，3）‎