2019年高考数学练习题汇总附加题满分练3

2019年高考数学练习题汇总附加题满分练3

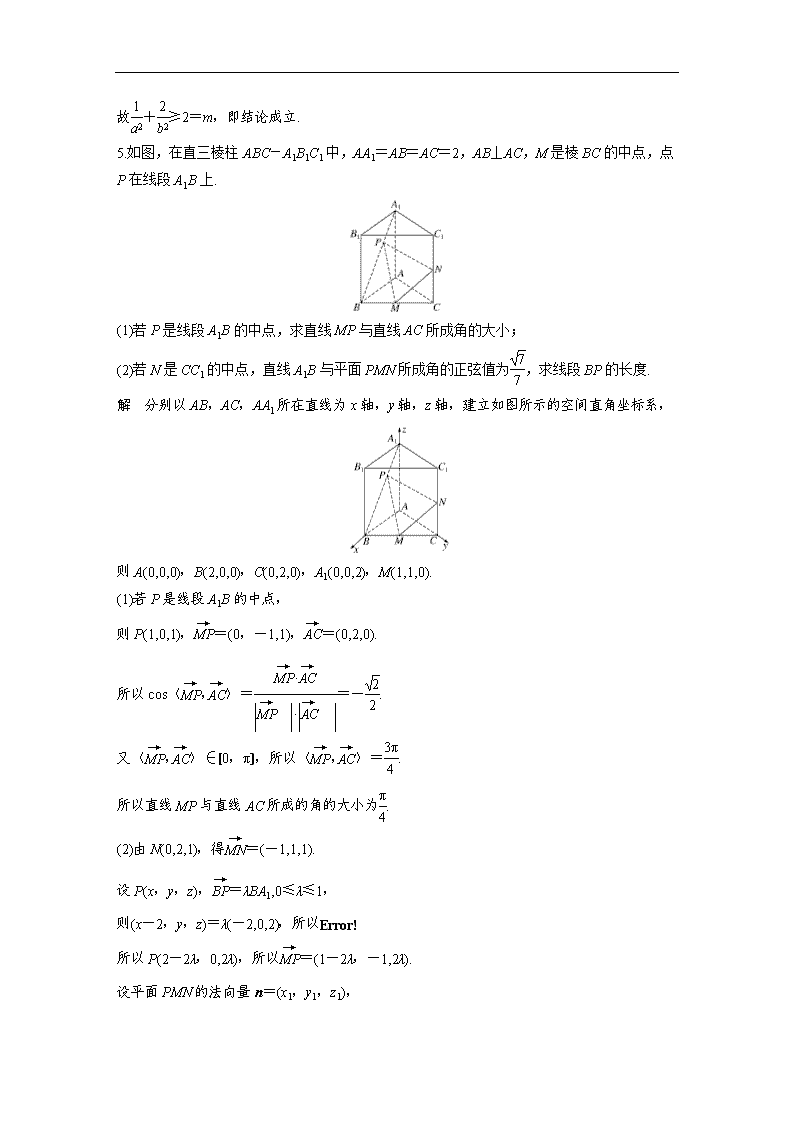
附加题满分练3‎ ‎1.如图，△ABC内接于⊙O，AB为⊙O的直径，BF是⊙O的切线，连结CF交⊙O于D，交AB于E.若BC＝BF＝4，CE∶ED＝6∶5，求⊙O的半径.‎ 解　如图，连结BD，‎ 因为BF是⊙O的切线，所以∠DBF＝∠BCF，‎ 因为BC＝BF，所以∠BCF＝∠BFC，‎ 所以∠DBF＝∠BFC，‎ 所以BD＝DF，又∠BEF＋∠BFC＝90°，∠EBD＋∠DBF＝90°，‎ 所以∠BEF＝∠EBD，所以BD＝ED，所以ED＝DF.‎ 设CE＝6x，ED＝5x(x>0)，则DF＝5x，‎ 因为BF＝4，根据切割线定理知BF2＝DF·CF，‎ 所以16＝5x×16x，解得x＝，‎ 所以EF＝ED＋DF＝2，‎ 因为BF为⊙O的切线，所以AB⊥BF，‎ 所以BE2＋BF2＝EF2，所以BE＝2，‎ 根据相交弦定理知AE·BE＝CE·ED，得AE＝3，‎ 所以AB＝5，‎ 因为AB为⊙O的直径，所以⊙O的半径为.‎ ‎2.若二阶矩阵M满足M＝，求曲线4x2＋4xy＋y2－12x＋12y＝0在矩阵M所对应的变换作用下得到的曲线的方程.‎ 解　记矩阵A＝，det(A)＝(－2)×(－1)－2×＝1≠0，‎ 故A－1＝，所以M＝A－1＝ ＝，‎ 即矩阵M＝.‎ 设曲线4x2＋4xy＋y2－12x＋12y＝0上任意一点P(x，y)在矩阵M对应的变换作用下得到点P′(x′，y′).‎ 所以＝ ＝，‎ 所以所以 又点P(x，y)在曲线4x2＋4xy＋y2－12x＋12y＝0上，代入整理得2x′2＋3y′＝0，‎ 由点P(x，y)的任意性可知，所求曲线的方程为2x2＋3y＝0.‎ ‎3.已知直线的极坐标方程为ρsin＝，圆M的参数方程为(其中θ为参数).‎ ‎(1)将直线的极坐标方程化为直角坐标方程；‎ ‎(2)求圆M上的点到直线的距离的最小值.‎ 解　(1)极点为直角坐标原点O，‎ ρsin＝ρ＝，‎ ‎∴ρsin θ＋ρcos θ＝1，其直角坐标方程为x＋y－1＝0.‎ ‎(2)将圆的参数方程化为普通方程为x2＋(y＋2)2＝4，圆心为M(0，－2)，‎ ‎∴点M到直线的距离为d＝＝＝，‎ ‎∴圆上的点到直线距离的最小值为.‎ ‎4.已知函数f(x)＝|x＋m|＋|x－2|(m>0)的最小值为4，正实数a，b满足＋＝.‎ 求证：＋≥m.‎ 证明　易知|x＋m|＋|x－2|≥|(x＋m)－(x－2)|＝|m＋2|，‎ 故由f(x)的最小值为4得|m＋2|＝4，又m>0，所以m＝2.‎ 又≥2＝3，当且仅当a＝，b＝时等号成立，‎ 故＋≥2＝m，即结论成立.‎ ‎5.如图，在直三棱柱ABC－A1B1C1中，AA1＝AB＝AC＝2，AB⊥AC，M是棱BC的中点，点P在线段A1B上.‎ ‎(1)若P是线段A1B的中点，求直线MP与直线AC所成角的大小；‎ ‎(2)若N是CC1的中点，直线A1B与平面PMN所成角的正弦值为，求线段BP的长度.‎ 解　分别以AB，AC，AA1所在直线为x轴，y轴，z轴，建立如图所示的空间直角坐标系，‎ 则A(0,0,0)，B(2,0,0)，C(0,2,0)，A1(0,0,2)，M(1,1,0).‎ ‎(1)若P是线段A1B的中点，‎ 则P(1,0,1)，＝(0，－1,1)，＝(0,2,0).‎ 所以cos〈，〉＝＝－.‎ 又〈，〉∈[0，π]，所以〈，〉＝.‎ 所以直线MP与直线AC所成的角的大小为.‎ ‎(2)由N(0,2,1)，得＝(－1,1,1). ‎ 设P(x，y，z)，＝λBA1,0≤λ≤1，‎ 则(x－2，y，z)＝λ(－2,0,2)，所以 所以P(2－2λ，0,2λ)，所以＝(1－2λ，－1,2λ).‎ 设平面PMN的法向量n＝(x1，y1，z1)，‎ 则n⊥，n⊥， ‎ 所以取n＝.‎ 因为BA1＝(－2,0,2)，设直线A1B与平面PMN所成的角为θ.‎ 由sin θ＝＝＝＝，得λ＝(舍负).‎ 所以＝BA1，所以BP＝BA1＝.‎ ‎6.已知n展开式的各项依次记为a1(x)，a2(x)，a3(x)，…，an(x)，an＋1(x).设F(x)＝a1(x)＋2a2(x)＋3a3(x)＋…＋nan(x)＋(n＋1)·an＋1(x).‎ ‎(1)若a1(x)，a2(x)，a3(x)的系数依次成等差数列，求n的值；‎ ‎(2)求证：对任意x1，x2∈[0,2]，恒有|F(x1)－F(x2)|≤2n－1(n＋2)－1.‎ ‎(1)解　依题意ak(x)＝Ck－1，k＝1,2,3，…，n＋1，‎ a1(x)，a2(x)，a3(x)的系数依次为C·0＝1，C·＝，C·2＝，‎ 所以2×＝1＋，解得n＝8或n＝1(舍去).‎ ‎(2)证明　F(x)＝a1(x)＋2a2(x)＋3a3(x)＋…＋nan(x)＋(n＋1)an＋1(x)＝C＋2C＋3C2＋…＋nCn－1＋(n＋1)Cn，‎ F(2)＝C＋2C＋3C＋…＋nC＋(n＋1)C，‎ 设Sn＝C＋2C＋3C＋…＋nC＋(n＋1)C，‎ 则Sn＝(n＋1)C＋nC＋…＋3C＋2C＋C，‎ 考虑到C＝C，将以上两式相加得 ‎2Sn＝(n＋2)(C＋C＋C＋…＋C＋C)，‎ 所以Sn＝2n－1(n＋2)，‎ 又当x∈[0,2]时，F′(x)>0恒成立，从而F(x)是[0,2]上的单调递增函数，‎ 所以对任意x1，x2∈[0,2]，|F(x1)－F(x2)|≤F(2)－F(0)＝2n－1(n＋2)－1.‎