数学理卷·2018届河南省南阳一中高三第六次考试试题

数学理卷·2018届河南省南阳一中高三第六次考试试题

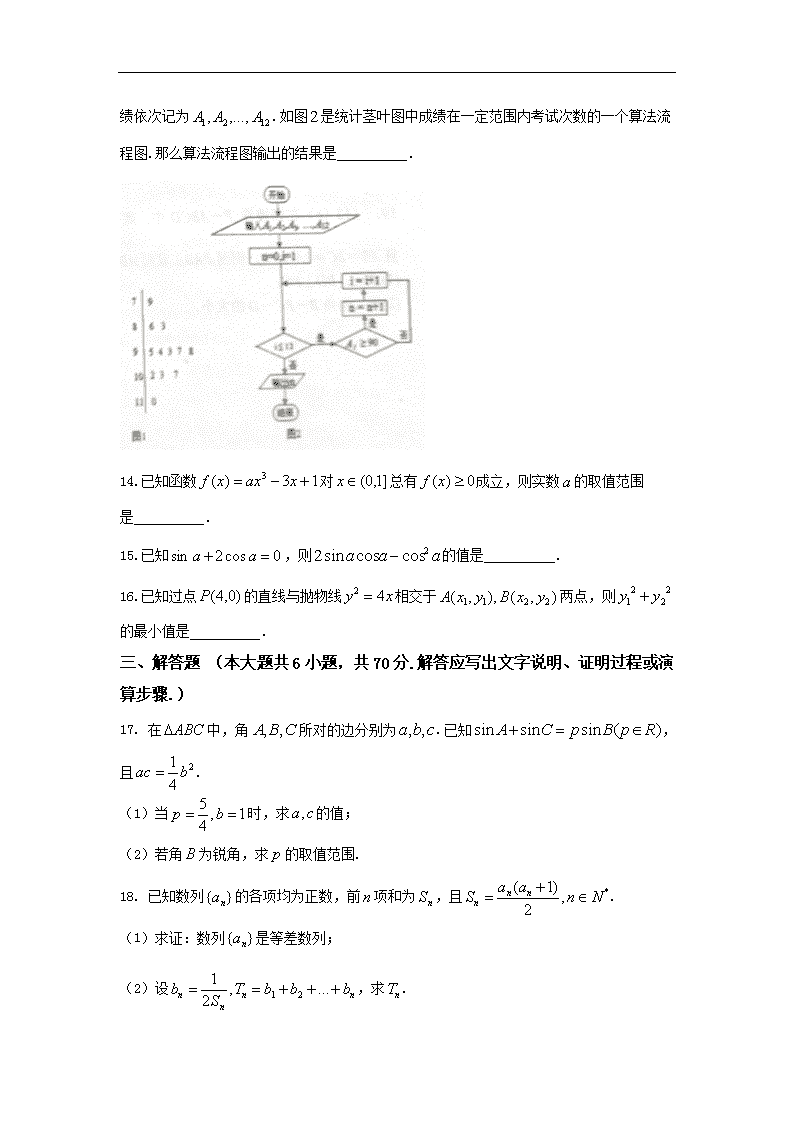
南阳一中2018级高三第六次考试 理数试题 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合，则（ ）‎ A． B． C． D．‎ ‎2.下面是关于复数的四个命题：的共轭复数为的虚部为，其中的真命题为（ ）‎ A． B． C． D．‎ ‎3.设，则“”是“直线与直线平行”的（ ）‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充分必要条件 D．既不充分也不必要条件 ‎ ‎4.在如图，所示的空间直角坐标系中，一个四面体的顶点坐标分别是 ‎.给出编号为①、②、③、④的四个图，则该四面体的正视图和俯视图分别为（ ）‎ A．①和② B．③和① C. ④和③ D．④和②‎ ‎5.设等差数列的前项和为，则（ ）‎ A． B． C. D．‎ ‎6.已知数列满足，则数列的前 项的和为（ ）‎ A． B． C. D．‎ ‎7.设双曲线的一个焦点为，虚轴的一个端点为，如果直线与该双曲线的一条渐近线垂直，那么此双曲线的离心率为（ ）‎ A． B． C. D．‎ ‎8.曲线在点处的切线与坐标轴所围三角形的面积为（ ）‎ A． B． C. D．‎ ‎9.已知函数为的零点，为图象的对称轴，且在上单调，则的最大值为（ ）‎ A． B． C. D．‎ ‎10.椭圆的左、右顶点分别为，点在上且直线斜率的取值范围是，那么直线斜率的取值范围是（ ）‎ A． B． C. D．‎ ‎11.样本的平均数为，样本的平均数为，若样本的平均数，则的大小关系为（ ）‎ A． B． C. D．不能确定 ‎12.函数的定义域是，对任意，则不等式的解集为（ ）‎ A． B． C. 或 D．或 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.如图是某高三学生进入高中三年来的数学考试成绩茎叶图，第次到第 次的数学成绩依次记为.如图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是 ．‎ ‎14.已知函数对总有成立，则实数的取值范围是 ．‎ ‎15.已知，则的值是 ．‎ ‎16.已知过点的直线与抛物线相交于两点，则的最小值是 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. 在中，角所对的边分别为.已知，且.‎ ‎（1）当时，求的值；‎ ‎（2）若角为锐角，求的取值范围.‎ ‎18. 已知数列的各项均为正数，前项和为，且.‎ ‎（1）求证：数列是等差数列；‎ ‎（2）设，求.‎ ‎19. 在四棱锥中，底面是直角梯形，，且，侧面底面是等边三角形.‎ ‎（1）求证：；‎ ‎（2）求二面角的大小.‎ ‎20. 已知椭圆过点，且离心率.‎ ‎（1）求椭圆的方程；‎ ‎（2）设直交椭圆于两点，判断点与以线段为直径的圆的位置关系，并说明理由.‎ ‎21. 已知函数.‎ ‎（1）若在上的最小值为，求的值；‎ ‎（2）若在上恒成立，求的取值范围.‎ ‎22. 已知关于的不等式（其中）.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若不等式在内有解，求实数的取值范围.‎ 南阳一中2015级高三第六次考试理数参考答案 一、选择题(共12小题,每小题5.0分,共60分) ‎ ‎1. B【解析】由得Q＝{x|x≥2或x≤－2}．∴∁RQ＝(－2,2)．又P＝[1,3]，∴P∪∁RQ＝[1,3]∪(－2,2)＝(－2,3]．‎ ‎2.C.z＝＝＝－1－i，所以|z|＝，p1为假命题；z2＝(－1－i)2＝(1＋i)2＝2i，p2为真命题；＝－1＋i，p3为假命题；p4为真命题．‎ ‎ ‎3A当a＝1时，直线l1：x＋2y－1＝0与l2：x＋(a＋1)y＋4＝0平行；反之由l1∥l2可得a＝1或a＝－2，‎ ‎4D由三视图可知，该几何体的正视图显然是一个直角三角形(三个顶点坐标分别是(0，0，2)，(0，2，0)，(0，2，2))且内有一虚线(一锐角顶点与一直角边中点的连线)，故正视图是④；俯视图是一个斜三角形，三个顶点坐标分别是(0，0，0)，(2，2，0)，(1，2，0)，故俯视图是②.‎ ‎5. C【解析】由Sm－1＝－2，Sm＝0，Sm＋1＝3，得am＝Sm－Sm－1＝2，am＋1＝Sm＋1－Sm＝3，所以等差数列的公差为d＝am＋1－am＝3－2＝1，‎ 由得解得 ‎6D【解析】由题意可得，所以数列{an}是等差数列，且公差是2，{bn}是等比数列，且公比是2．又a1=1，所以an=a1+（n﹣1）d=2n﹣1．所以=b1•22n﹣2=22n﹣2．‎ 设cn=，所以cn=22n﹣2，所以，所以数列{cn}是等比数列，且公比为4，首项为1．‎ 由等比数列的前n项和的公式得：其前10 项的和为．故选D．‎ ‎7. D【解析】设双曲线方程为－＝1(a>0，b>0)，如图所示，双曲线的一条渐近线方程为y＝x，‎ 而kBF＝－，∴·(－)＝－1，整理得b2＝ac.∴c2－a2－ac＝0，两边同除以a2，得e2－e－1＝0，解得e＝或e＝(舍去)，故选D.‎ ‎8.D ‎9. B因为x＝－为f(x)的零点，x＝为f(x)的图象的对称轴，所以－＝＋kT，即＝T＝·，所以ω＝4k＋1(k∈N)，又因为f(x)在上单调，所以－＝≤＝，即ω≤12，由此得ω的最大值为9，故选B.‎ ‎10.B椭圆的左、右顶点分别为(－2，0)，(2，0)，设P(x0，y0)，则＝·＝，而，即＝ (4－)，所以＝－，所以kPA1∈‎ ‎11. A依题意得x1＋x2＋…＋xn＝n，y1＋y2＋…＋ym＝m，x1＋x2＋…＋xn＋y1＋y2＋…＋ym＝(m＋n)＝(m＋n)α＋(m＋n)(1－α)，所以n＋m＝(m＋n)α＋(m＋n)(1－α)，‎ 所以于是有n－m＝(m＋n)[α－(1－α)]＝(m＋n)(2α－1)．‎ 因为0＜α＜，所以2α－1＜0.所以n－m＜0，即n＜m.‎ ‎12. A【解析】构造函数g(x)＝ex·f(x)－ex，因为g′(x)＝ex·f(x)＋ex·f′(x)－ex＝ex[f(x)＋f′(x)]－ex>ex－ex＝0，所以g(x)＝ex·f(x)－ex为R上的增函数，又因为g(0)＝e0·f(0)－e0＝1，所以原不等式转化为g(x)>g(0)，解得x>0.‎ 二、填空题(共4小题,每小题5.0分,共20分) ‎ ‎13【答案】9【解析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加12次考试成绩超过90分的人数；根据茎叶图的含义可得超过90分的人数为9个 ‎ 14.【答案】[4，＋∞)【解析】当x∈(0,1]时不等式ax3－3x＋1≥0可化为 a≥，设g (x)＝，x∈(0,1]，g′(x)＝＝－，‎ 因此g(x)的最大值为4，则实数a的取值范围是[4，＋∞)．‎ ‎ 15.【答案】－1【解析】sinα＋2cosα＝0，∴sinα＝－2cosα，∴tanα＝－2，‎ 又∵2sinαcosα－cos2α＝＝，∴原式＝＝－1.‎ ‎16【答案】32【解析】当直线的斜率不存在时，直线方程为x＝4，代入y2＝4x，得交点为(4,4)，(4，－4)，∴＋＝16＋16＝32.当直线斜率存在时，设直线方程为y＝k(x－4)，与y2＝4x联立，消去x得ky2－4y－16k＝0.由题意知k≠0，则y1＋y2＝，y1y2＝－16.∴＋＝(y1＋y2)2－2y1y2＝＋32>32.‎ 三、解答题：共6小题 ，70分。应写出必要的文字说明或推理，验算过程 ‎ ‎17【答案】（Ⅰ）或；（Ⅱ）‎ ‎【解析】（Ⅰ）由题设并利用正弦定理，得…………3分解得或…………6分 ‎（Ⅱ）由余弦定理，b2=a2+c2‎-2ac cosB=(a+c)2‎-2ac cosB…=p2b2-即……9分，因为，得，…………11分 由题设知，所以…………12分 ‎18【答案】（1）证明见解析；(2)Tn＝【解析】(1)证明　∵Sn＝，n∈N，‎ ‎∴当n＝1时，a1＝S1＝(an>0)，∴a1＝1.当n≥2时，由 得2an＝a＋an－a－an－1，即(an＋an－1)(an－an－1－1)＝0，∵an＋an－1>0，∴an－an－1＝1(n≥2)．‎ 所以数列{an}是以1为首项，1为公差的等差数列．‎ ‎(2)解　由(1)可得an＝n，Sn＝，∴bn＝＝＝－.‎ ‎∴Tn＝b1＋b2＋b3＋…＋bn＝1－＋－＋…＋－＝1－＝.‎ ‎19 【答案】(2).【解析】方法一：(1)证明：取AB中点为O，连结PO，OC，∵△PAB是等边三角形，∴PO⊥AB，又∵侧面PAB⊥底面ABCD，∴PO⊥底面ABCD，∴OC为PC在底面ABCD上的射影．又∵AB＝BC＝2AD＝2，∠ABC＝∠DAB＝，∴△DAB≌△OBC，∴∠BCO＝∠DBA，又∵∠ABD＋∠CBD＝90°，∴∠CBD＋∠BCO＝90°.∴BD⊥OC，∴BD⊥PC.‎ ‎(2)取PC中点E，连结BE，DE，∵PB＝BC，∴BE⊥PC.又∵BD⊥PC，BE∩BD＝B，∴PC⊥平面BDE，∴PC⊥DE，∴∠BED是二面角B－PC－D的平面角．∵AB＝BC＝2AD＝2，∠ABC＝，∴BE＝PE＝PC＝，PD＝BD＝.∴DE＝，∴BE2＋DE2＝BD2，∴∠BED＝，∴二面角B－PC－D的大小为.‎ 方法二：(1)证明：取AB中点为O，CD中点为M，连结OM，PO，‎ ‎∵△PAB是等边三角形，∴PO⊥AB，又∵侧面PAB⊥底面ABCD，‎ ‎∴PO⊥底面ABCD，∴以O为坐标原点，建立空间直角坐标系．如图，‎ ‎∵AB＝BC＝2AD＝2，△PAB是等边三角形，∴OP＝，‎ ‎∴O(0，0，0)，B(1，0，0)，C(1，2，0)，D(－1，1，0)，P(0，0，)．‎ ‎∴＝(－2，1，0)，＝(1，2，－)．∵·＝－2＋2＝0，∴BD⊥PC.‎ ‎(2)设平面PBC的法向量为＝(x1，y1，z1)．∵＝(1，0，－)，＝(0，2，0)，∴令z1＝1，则x1＝，y1＝0，∴＝(，0，1)．设平面PCD 的法向量为＝(x2，y2，z2)，∵＝(2，1，0)，＝(1，－1，)，∴令x2＝1，则y2＝－2，z2＝－，∴＝(1，－2，－)．∴cos〈，〉＝＝＝0，∴〈 ，〉＝，∴二面角B－PC－D的大小为.‎ ‎20. 【答案】法一　(1)由已知得，‎ 解得所以椭圆E的方程为＋＝1.‎ ‎(2)设A(x1，y1)，B(x2，y2)，AB的中点为H(x0，y0)．由得(m2＋2)y2－2my－3＝0.‎ 所以y1＋y2＝，y1y2＝－，从而y0＝.‎ 所以|GH|2＝2＋y＝2＋y＝(m2＋1)y＋my0＋.‎ ‎＝＝＝‎ ‎＝(1＋m2)(y－y1y2)，故|GH|2－＝my0＋(1＋m2)y1y2＋＝－＋＝＞0，所以|GH|＞.故点G在以AB为直径的圆外．‎ 法二　(1)同法一．(2)设点A(x1，y1)，B(x2，y2)，则＝，＝.‎ 由得(m2＋2)y2－2my－3＝0，所以y1＋y2＝，y1y2＝－，‎ 从而·＝＋y1y2＝＋y1y2‎ ‎＝(m2＋1)y1y2＋m(y1＋y2)＋＝＋＋＝＞0，‎ 所以cos〈，〉＞0.又，不共线，所以∠AGB为锐角．故点G在以AB为直径的圆外．‎ ‎21.(1) f′(x)＝.‎ ‎①若a≥－1，则x＋a≥0，即f′(x)≥0在[1，e]上恒成立，‎ 此时f(x)在[1，e]上为增函数，∴f(x)min＝f(1)＝－a＝，∴a＝－(舍去)．‎ ‎②若a≤－e，则x＋a≤0，即f′(x)≤0在[1，e]上恒成立，‎ 此时f(x)在[1，e]上为减函数，∴f(x)min＝f(e)＝1－＝，∴a＝－(舍去)．‎ ‎③若－e0，∴f(x)在(－a，e)上为增函数，‎ ‎∴f(x)min＝f(－a)＝ln(－a)＋1＝，∴a＝－.综上所述，a＝－.‎ ‎(3)∵f(x)0，∴a>xln x－x3.令g(x)＝xln x－x3，h(x)＝g′(x)＝1＋ln x－3x2，‎ h′(x)＝－6x＝.∵x∈(1，＋∞)时，h′(x)<0，∴h(x)在(1，＋∞)上是减函数．‎ ‎∴h(x)1时，x≤0，此时x不存在．∴不等式的解集为{x|－4≤x≤}．‎ ‎(2)∵设f(x)＝|2x＋1|－|x－1|＝‎ ‎∴f(x)∈[－，＋∞)，即f(x)的最小值为－.若f(x)≤log‎2a有解，则log‎2a≥－，‎ 解得即a的取值范围是