2020届高考理科数学二轮专题复习课件：专题6 统计与概率2-6-解答题 3

2020届高考理科数学二轮专题复习课件：专题6 统计与概率2-6-解答题 3

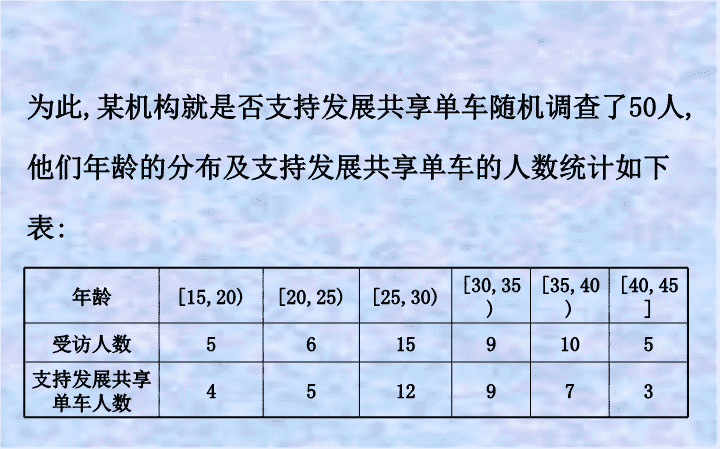
第 3 课时　　 概率与统计案例的综合应用 考向一　概率与独立性检验 【例 1 】 共享单车为很多市民解决了出行难题 . 然而 , 这种模式也遇到了一些让人尴尬的问题 , 比如乱停乱放 , 或将共享单车占为“私有”等 . 为此 , 某机构就是否支持发展共享单车随机调查了 50 人 , 他们年龄的分布及支持发展共享单车的人数统计如下表 : 年龄 [15,20) [20,25) [25,30) [30,35) [35,40) [40,45] 受访人数 5 6 15 9 10 5 支持发展共享单车人数 4 5 12 9 7 3 (1) 由以上统计数据填写下面的 2×2 列联表 , 并判断能 否在犯错误的概率不超过 0.1 的前提下 , 认为 年龄与是 否支持发展共享单车有关系 ① . 年龄低于 35 岁 年龄不低于 35 岁 总计 支持 不支持 总计 (2) 若对年龄在 [15,20),[20,25) 的被调查人中各随机 选取 2 人进行调查 , 记选中的 4 人中支持发展共享单车的 人数为 X, 求 随机变量 X 的分布列及数学期望 ② . 参考数据 : P(K 2 ≥k 0 ) 0.15 0.10 0.05 k 0 2.072 2.706 3.841 参考公式 : K 2 = , 其中 n=a+b+c+d. 【题眼直击】 题眼 思维导引 ① 想到利用 K 2 公式求解 ② 想到利用数学期望公式求解 【解析】 (1) 根据所给数据得到如下 2×2 列联表 : 年龄低于 35 岁 年龄不低于 35 岁 总计 支持 30 10 40 不支持 5 5 10 总计 35 15 50 根据 2×2 列联表中的数据 , 得到 K 2 的观测值 k= ≈2.38<2.706. 所以不能在犯错误的概率不超过 0.1 的前提下 , 认为年 龄与是否支持发展共享单车有关系 . (2) 由题意 , 年龄在 [15,20) 的 5 个受访人中 , 有 4 人支持发展共享单车 ; 年龄在 [20,25) 的 6 个受访人中 , 有 5 人支持发展共享单车 . 所以随机变量 X 的所有可能取值为 2,3,4. 因为 P(X=2)= ,P(X=3)= , P(X=4)= , 所以随机变量 X 的分布列为 X 2 3 4 P 所以随机变量 X 的数学期望 E(X)=2× +3× +4× = . 【拓展提升】 　独立性检验的步骤 (1) 根据样本数据制成 2×2 列联表 . (2) 计算 K 2 的观测值 k. (3) 比较临界值的大小关系作统计判断 . 【变式训练】　 当今信息时代 , 众多高中生也配上了手机 , 某校为研究经常使用手机是否对学习成绩有影响 , 随机抽取高三年级 50 名理科生的一次数学周练成绩 , 用茎叶图表示如图所示 ( 记 60 分为及格 ): (1) 根据茎叶图中数据完成下面的 2×2 列联表 , 并判断是否有 95% 的把握认为经常使用手机对学习成绩有影响 ? 及格 不及格 总计 很少使用手机 经常使用手机 总计 (2) 从 50 人中 , 选取一名很少使用手机的同学记为甲和 一名经常使用手机的同学记为乙 , 解一道数列题 , 甲、 乙独立解决此题的概率分别为 p 1 ,p 2 , 且 p 2 =0.4, 若 p 1 - p 2 ≥0.3, 则此二人适合结为学习上互帮互助的“师 徒” , 记 X 为两人中解决此题的人数 , 若 E(X)=1.12, 问两 人是否适合结为“师徒” ? 参考公式及数据 :K 2 = , 其中 n=a+b+c+d, P(K 2 ≥k 0 ) 0.10 0.05 0.025 k 0 2.706 3.841 5.024 【解析】 (1) 由茎叶图数据 , 得 2×2 列联表 : 及格 不及格 总计 很少使用手机 20 7 27 经常使用手机 10 13 23 总计 30 20 50 由列联表可得 :K 2 的观测值 k= ≈4.844 >3.841, 所以有 95% 的把握认为经常使用手机对学习成绩有影响 . (2) 依题意 , 随机变量 X 的可能取值为 0,1,2. 则 P(X=0)=(1-p 1 )(1-p 2 ),P(X=2)=p 1 p 2 , P(X=1)=(1-p 1 )p 2 +p 1 (1-p 2 ), 所以随机变量 X 的分布列为 X 0 1 2 P (1-p 1 )(1-p 2 ) (1-p 1 )p 2 +p 1 (1-p 2 ) p 1 p 2 所以 E(X)=(1-p 1 )p 2 +p 1 (1-p 2 )+2p 1 p 2 =p 1 +p 2 =1.12, 所以 p 1 =1.12-p 2 =0.72, 因此 p 1 -p 2 =0.72-0.4=0.32>0.3, 两人适合结为“师徒” . 考向二　概率与回归分析 【例 2 】 某市房地产相关数据显示 ,2016 年该市新建住宅销售均价走势如图所示 ,3 月至 7 月房价上涨过快 , 政府从 8 月份开始采取宏观调控措施 ,10 月份开始房价得到很好控制 . 世纪金榜导学号 (1) 根据房地产数据发现 ,3 月份至 7 月份的各月均价 y( 万元 / 平方米 ) 与月份 x 之间具有较强的线性相关关系 , 试建立 y 关于 x 的回归方程 ① ; 若政府不调控 , 依此相关 关系预测 12 月份该市新建住宅的销售均价 . (2) 房地产数据研究所在 2016 年的 12 个月份中 , 随机抽取 3 个月的数据进行样本分析 , 若关注所抽 3 个月份的所属季度 , 记不同季度的个数为 X, 求 X 的分布列和数学期望 ② . 参考数据 : , , =0.64. 参考公式 : 回归直线 x+ 的斜率和截距的最小 二乘估计分别为 = , = . 【题眼直击】 题眼 思维导引 ① 想到利用最小二乘法求回归直线方程 ② 想到利用数学期望公式求解 【解析】 (1) 月份 x 3 4 5 6 7 均价 y ( 万元 / 平方米 ) 0.95 0.98 1.11 1.12 1.20 计算可得 , , 所以 = =0.064, = - =1.072-0.064× 5=0.752. 所以 y 关于 x 的回归方程为 =0.064x+0.752. 将 x=12 代入回归方程 , 得 =0.064×12+0.752=1.52, 所以预测 12 月份该市新建住宅的销售均价约为 1.52 万元 / 平方米 . (2) 根据题意 ,X 的可能取值为 1,2,3. P(X=1)= , P(X=2)=1-P(X=1)-P(X=3)= , 所以 X 的分布列为 X 1 2 3 P 因此 ,X 的数学期望 E(X)=1× +2× +3× = . 【拓展提升】 　求回归直线方程的步骤 (1) 依据样本数据画出散点图 , 确定两个变量具有线性 相关关系 ( 有时可省略 ). (2) 计算出 的值 . (3) 计算回归系数 . (4) 写出回归直线方程 . 【变式训练】 假设关于某设备的使用年限 x( 年 ) 和所支出的维修费用 y( 万元 ) 有如下表的统计资料 : 使用年限 x/ 年 2 3 4 5 6 维修费用 y/ 万元 2.2 3.8 5.5 6.5 7.0 若由资料可知 y 对 x 呈线性相关关系 , 试求 : (1) 线性回归方程 . (2) 根据线性回归方程 , 估计使用年限为 12 年时 , 维修费用是多少 ? 【解析】 (1) 列表 i 1 2 3 4 5 总计 x i 2 3 4 5 6 20 y i 2.2 3.8 5.5 6.5 7.0 25 x i y i 4.4 11.4 22.0 32.5 42.0 112.3 4 9 16 25 36 90 = 于是 = - =5-1.23×4=0.08. 所以线性回归方程为 =1.23x+0.08. (2) 当 x=12 时 , =1.23×12+0.08=14.84( 万元 ), 即估计使用 12 年时 , 维修费用是 14.84 万元 .