四川省遂宁市2020届高三第三次诊断考试 数学（理）

四川省遂宁市2020届高三第三次诊断考试 数学（理）

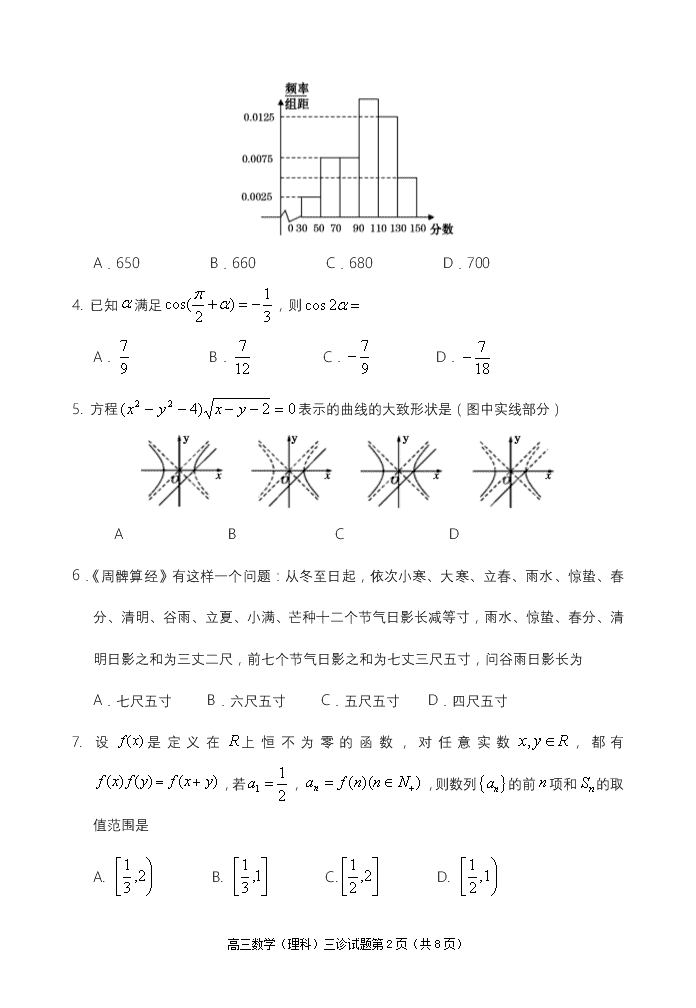
‎ 遂宁市高中2020届三诊考试 ‎ 数学（理科）试题 本试卷分第I卷（选择题）和第II卷（非选择题）两部分。总分150分。考试时间120分钟。‎ 第Ⅰ卷（选择题，满分60分）‎ 注意事项：‎ ‎1．答题前，考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。并检查条形码粘贴是否正确。‎ ‎2．选择题使用2B铅笔填涂在答题卡对应题目标号的位置上，非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。‎ ‎3．考试结束后，将答题卡收回。‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每个小题给出的四个选项中，只有一个是符合题目要求的。‎ ‎1．设，则“”是“”的 A．充分而不必要条件 B．必要而不充分条件 ‎ C．充要条件 D．既不充分也不必要条件 ‎2．若复数为纯虚数（为虚数单位,为实数），则的值为 A． B． C． D．1‎ ‎3．某人口大县举行“《只争朝夕，决战决胜脱贫攻坚》扶贫知识政策答题比赛”，分初赛和复赛两个阶段进行，规定：初赛成绩大于90分的具有复赛资格，某校有1000名学生参加了初赛，所有学生的成绩均在区间（30，150]内，其频率分布直方图如图所示，则获得复赛资格的人数为 高三数学（理科）三诊试题第8页（共8页）‎ A．650 B．660 C．680 D．700‎ ‎4. 已知满足，则 A． B． C． D．‎ ‎5. 方程表示的曲线的大致形状是（图中实线部分）‎ A B C D ‎6．《周髀算经》有这样一个问题：从冬至日起，依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸，雨水、惊蛰、春分、清明日影之和为三丈二尺，前七个节气日影之和为七丈三尺五寸，问谷雨日影长为 A．七尺五寸 B．六尺五寸 C．五尺五寸 D．四尺五寸 ‎7. 设是定义在上恒不为零的函数，对任意实数，都有，若，，则数列的前项和的取值范围是 A. B. C. D. ‎ 高三数学（理科）三诊试题第8页（共8页）‎ ‎8. 2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最，编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”，见证着人民军队迈向世界一流军队的坚定步伐，其中空中梯队编有12个梯队，在领队机梯队、预警指挥机梯队、轰炸机梯队、舰载机梯队、歼击机梯队、陆航突击梯队这6个梯队中，某学校为宣传的需要，要求甲同学需从中选3个梯队了解其组成情况，其中舰载机梯队、歼击机梯队两个梯队中至少选择一个，则不同的选法种数为．‎ A．12种 B．16种 C．18种 D．20种 ‎9. 设函数，若，，，则的大小关系为 A． B．‎ C． D．‎ ‎10. 已知正三棱柱的底面边长为，且该三棱柱外接球的表面积为，若为底面的中心，则与平面所成角的大小为 A． B． C． D．‎ ‎11. 已知，是双曲线的左、右焦点，若双曲线上存在点满足，则双曲线离心率的最小值为 A． B． C． D． ‎ ‎12. 已知函数若存在使得 高三数学（理科）三诊试题第8页（共8页）‎ ‎，则实数的最大值为 A． B． C． D．‎ 第Ⅱ卷（非选择题，满分90分）‎ 注意事项：‎ ‎1．请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答，不能答在此试卷上。‎ ‎2．试卷中横线及框内注有“▲”的地方，是需要你在第Ⅱ卷答题卡上作答。‎ 本卷包括必考题和选考题两部分。第13题至第21题为必考题，每个试题考生都作答；第22、23题为选考题，考生根据要求作答。‎ 二、填空题：本大题共4个小题，每小题5分，共20分。‎ ‎13. 曲线在点处的切线的倾斜角为 ▲ 。‎ ‎14．已知两个单位向量、的夹角为，向量，则 ▲ 。‎ ‎15．已知点，过抛物线的焦点的直线交抛物线于，两点，若，则点的纵坐标为 ▲ 。‎ ‎16. 如图，平行六面体中，，，，，，则的长为 ‎ ▲ 。‎ 三、解答题：本大题共70分。解答应写出文字说明、证明过程或演算步骤。‎ ‎17．（本小题满分12分）‎ 高三数学（理科）三诊试题第8页（共8页）‎ 函数的部分图象如图所示，又函数 ‎（1）求函数的单调增区间；‎ ‎（2）设的内角，，的对边分别为，，，又，且锐角满足，若，为边的中点，求的周长。‎ ‎▲‎ ‎18.（本小题满分12分）‎ 如图，在长方体中，底面是边长为的正方形，对角线与相交于点，‎ 点在线段上，且，‎ 与底面所成角为。‎ ‎（1）求证：；‎ ‎（2）求二面角的余弦值；‎ ‎（3）设点在线段上，且∥平面，求的长。‎ ‎▲‎ 高三数学（理科）三诊试题第8页（共8页）‎ ‎19. （本小题满分12分）‎ 某中学举行“新冠肺炎”防控知识闭卷考试比赛，总分获得一等奖、二等奖、三等奖的代表队人数情况如下表，其中一等奖代表队比三等奖代表队多10人。该校政教处为使颁奖仪式有序进行，气氛活跃，在颁奖过程中穿插抽奖活动。并用分层抽样的方法从三个代表队中共抽取16人在前排就坐，其中二等奖代表队有5人（同队内男女生仍采用分层抽样）‎ 名次 性别 一等奖 代表队 二等奖 代表队 三等奖 代表队 男生 ‎？‎ ‎30‎ ‎◎‎ 女生 ‎30‎ ‎20‎ ‎30‎ ‎（1）从前排就坐的一等奖代表队中随机抽取人上台领奖，用表示女生上台领奖的人数，求的分布列和数学期望。‎ ‎（2）抽奖活动中，代表队员通过操作按键，使电脑自动产生内的两个均匀随机数，，随后电脑自动运行如图所示的程序框图的相应程序。若电脑显示“中奖”，则代表队员获相应奖品；若电脑显示“谢谢”，则不中奖。求代表队队员获得奖品的概率。‎ ‎▲‎ ‎20.（本小题满分12分）‎ 已知函数.‎ ‎（1）判断函数在区间上零点的个数，并说明理由。‎ ‎（2）当时，‎ 高三数学（理科）三诊试题第8页（共8页）‎ ①比较与的大小关系，并说明理由；‎ ②证明：。‎ ‎▲‎ ‎21.（本小题满分12分）‎ 如图，定义：以椭圆中心为圆心，长轴为直径的圆叫做椭圆的“辅助圆”。过椭圆第四象限内一点作轴的垂线交其“辅助圆”于点，当点在点的下方时，称点为点的“下辅助点”。已知椭圆上的点的下辅助点为。‎ ‎（1）求椭圆的方程；‎ ‎（2）若的面积等于，求下辅助点的坐标；‎ ‎（3）已知直线：与椭圆交于不同的，两点，若椭圆上存在点，使得四边形是对边平行且相等的四边形。求直线与坐标轴围成的三角形面积最小时的的值。‎ ‎▲‎ 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题计分。‎ ‎22．（本小题满分10分）选修4—4：坐标系与参数方程 高三数学（理科）三诊试题第8页（共8页）‎ 在平面直角坐标系中，将曲线方程，先向左平移个单位，再向上平移个单位，得到曲线。‎ ‎（1）点为曲线上任意一点，写出曲线的参数方程，并求出的最大值；‎ ‎（2）设直线l的参数方程为，（为参数），又直线与曲线的交点为，，以坐标原点为极点，轴正半轴为极轴建立极坐标系，求过线段的中点且与垂直的直线的极坐标方程。‎ ‎▲‎ ‎23．（本小题满分10分）选修4—5：不等式选讲 已知函数， ‎ ‎（1）解不等式；‎ ‎（2）当，时，若的值域为，求证：。‎ ‎▲‎ 高三数学（理科）三诊试题第8页（共8页）‎