山西省太原市2020年高三年级模拟试题（一）文科数学

山西省太原市2020年高三年级模拟试题（一）文科数学

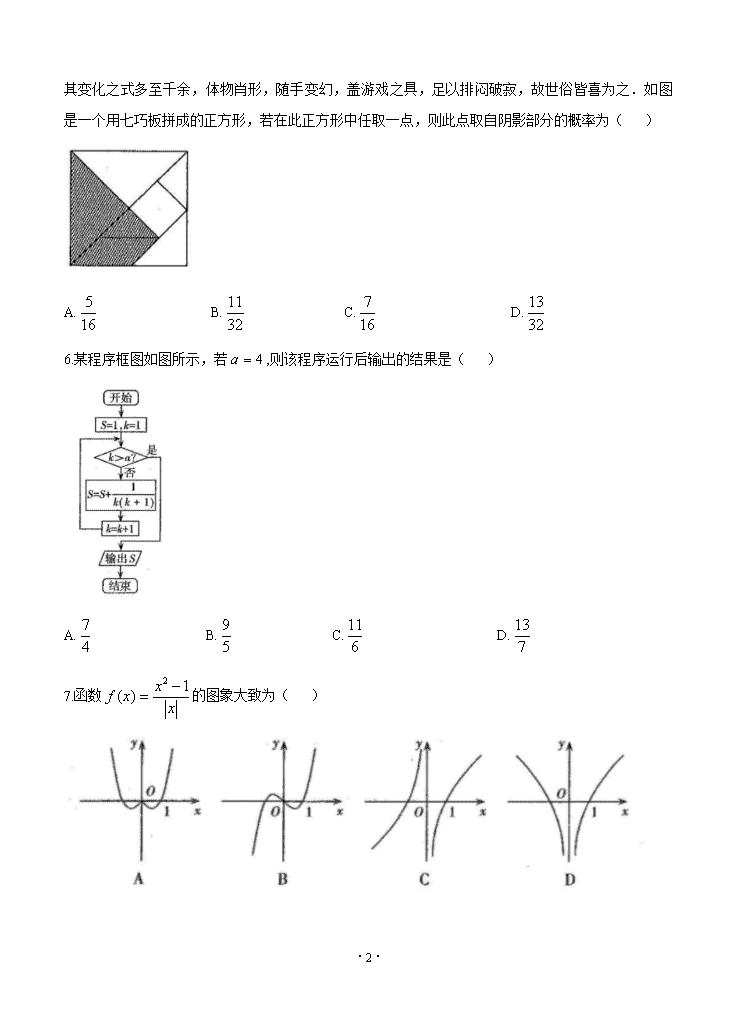
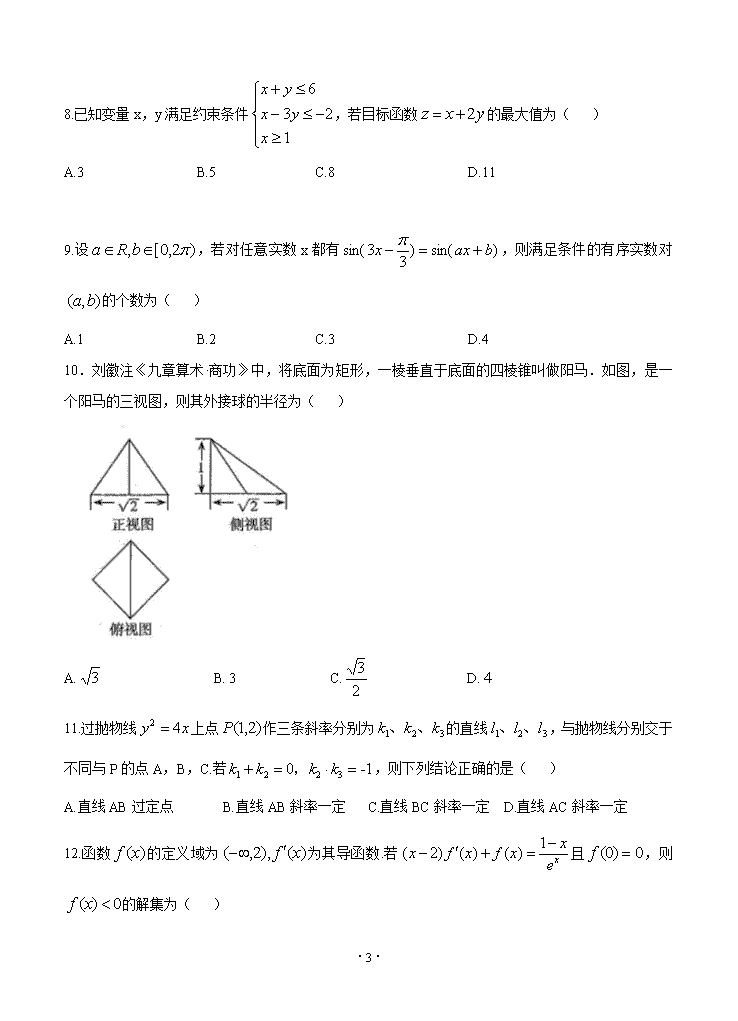
太原市2020年高三年级模拟试题（一）‎ 数学试卷（文科）‎ ‎（考试时间：下午3：00——5：00）‎ 注意事项：‎ ‎1．本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，第I卷1至4页，第Ⅱ卷5至8页。‎ ‎2．回答第I卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎3．回答第I卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，写在本试卷上无效。‎ ‎4．回答第Ⅱ卷时，将答案写在答题卡相应位置上，写在本试卷上无效。‎ ‎5．考试结束后，将本试卷和答题卡一并交回。‎ 第Ⅰ卷 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.若全集，集合，，则=（ ）‎ A. B. C. D.‎ ‎2.已知i是虚数单位，复数在复平面内对应的点在第二象限，则实数m的取值范围是（ ）‎ A. B. C. D.‎ ‎3.已知等差数列中，前5项和，则（ ）‎ A.16 B‎.17 C.18 D.19‎ ‎4.已知平面向量，若与垂直，则（ ）‎ A. B‎.2 C. D.1‎ ‎5.七巧板是中国古代劳动人民发明的一种传统智力玩具，它由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成．（清）陆以湉《冷庐杂识》卷中写道：近又有七巧图，其式五，其数七，‎ ‎·12·‎ 其变化之式多至千余，体物肖形，随手变幻，盖游戏之具，足以排闷破寂，故世俗皆喜为之．如图是一个用七巧板拼成的正方形，若在此正方形中任取一点，则此点取自阴影部分的概率为（ ）‎ A. B. C. D.‎ ‎6.某程序框图如图所示，若,则该程序运行后输出的结果是（ ）‎ A. B. C. D.‎ ‎7.函数的图象大致为（ ）‎ ‎·12·‎ ‎8.已知变量x，y满足约束条件，若目标函数的最大值为（ ）‎ A.3 B‎.5 C.8 D.11‎ ‎9.设，若对任意实数x都有，则满足条件的有序实数对的个数为（ ）‎ A.1 B‎.2 C.3 D.4‎ ‎10．刘徽注《九章算术·商功》中，将底面为矩形，一棱垂直于底面的四棱锥叫做阳马．如图，是一个阳马的三视图，则其外接球的半径为（ ）‎ A. B. C. D.‎ ‎11.过抛物线上点作三条斜率分别为的直线，与抛物线分别交于不同与P的点A，B，C.若，则下列结论正确的是（ ）‎ A.直线AB过定点 B.直线AB斜率一定 C.直线BC斜率一定 D.直线AC斜率一定 ‎12.函数的定义域为为其导函数.若且，则的解集为（ ）‎ ‎·12·‎ A. B. C. D.‎ 第Ⅱ卷（非选择题共90分）‎ 本卷包括必考题和选考题两部分，第13题～第21题为必考题，每个试题考生都必须作答，第22题、第23题为选考题，考生根据要求作答．‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13.双曲线的实轴长是 .‎ ‎14.已知函数是偶函数，则= ‎ ‎15.在如图所示装置中，正方形框架的边长都是1，且平面ABCD与平面ABEF互相垂直，活动弹子M，N分别在正方形对角线AC，BF上移动，则MN长度的最小值是 .‎ ‎16.我们知道，裴波那契数列是数学史上一个著名数列，在裴波那契数列中，.用表示它的前n项和，若已知，那么 ‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．‎ ‎（一）必考题；共60分．‎ ‎17．（本小题满分12分）‎ ‎ 手机运动计步已成为一种时尚，某中学统计了该校教职工一天走步数（单位：百步），绘制出如下频率分布直方图：‎ ‎（Ⅰ）求直方图中a的值，并由频率分布直方图估计该校教职工一天步行数的中位数；‎ ‎（Ⅱ）若该校有教职工175人，试估计一天行走步数不大于130百步的人数；‎ ‎·12·‎ ‎（Ⅲ）在（Ⅱ）的条件下，该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动，再从6人中选取2人担任领队，求着两人均来自区间的概率.‎ ‎18.（本小题满分12分）‎ ‎ 已知△ABC中，a，b，c分别是内角A，B，C的对边，.‎ ‎（Ⅰ）求C；‎ ‎（Ⅱ）若的面积为，求的值.‎ ‎19.（本小题满分12分）‎ ‎ 如图（1），在等腰直角△ABC中，，点D为AB中点，将△ADC沿DC折叠得到三棱锥，如图（2），其中，点M，N，G分别为的中点.‎ ‎（Ⅰ）求证：MN⊥平面DCG；‎ ‎（Ⅱ）求三棱锥的体积.‎ ‎·12·‎ ‎20.（本小题满分12分）‎ ‎ 已知函数 ‎（Ⅰ）求曲线在点处的切线方程；‎ ‎（Ⅱ）证明：在上有且仅有2个零点.‎ ‎21.（本小题满分12分）‎ ‎ 椭圆E的焦点为和，过的直线交E于A，B两点，过A作与y轴垂直的直线，又知点，直线BH记为，与交于点C.设，已知当时，.‎ ‎（Ⅰ）求椭圆E的方程；‎ ‎（Ⅱ）求证：无论如何变化，点C的横坐标是定值，并求出这个定值.‎ ‎（二）选考题：共10分，请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑．‎ ‎·12·‎ ‎22．（本小题满分10分）[选修4-4:坐标系与参数方程]‎ 在平面直角坐标系xOy中，曲线的参数方程为（为参数），已知点Q（6，0），点P是曲线上任意一点，点M满足，以坐标原点为极点，x轴正半轴为极轴建立极坐标系．‎ ‎（I）求点M的轨迹的极坐标方程；‎ ‎（Ⅱ）已知直线与曲线交于A，B两点，若，求k的值 ‎23．（本小题满分10分）[选修4-5:不等式选讲]‎ 已知函数.‎ ‎（I）若的最小值为1，求实数a的值；‎ ‎（Ⅱ）若关于x的不等式f（x）+g（x）<1的解集包含，求实数a的取值范围.‎ ‎·12·‎ ‎·12·‎ ‎·12·‎ ‎·12·‎ ‎·12·‎ ‎·12·‎