- 2021-06-19 发布 |
- 37.5 KB |
- 7页

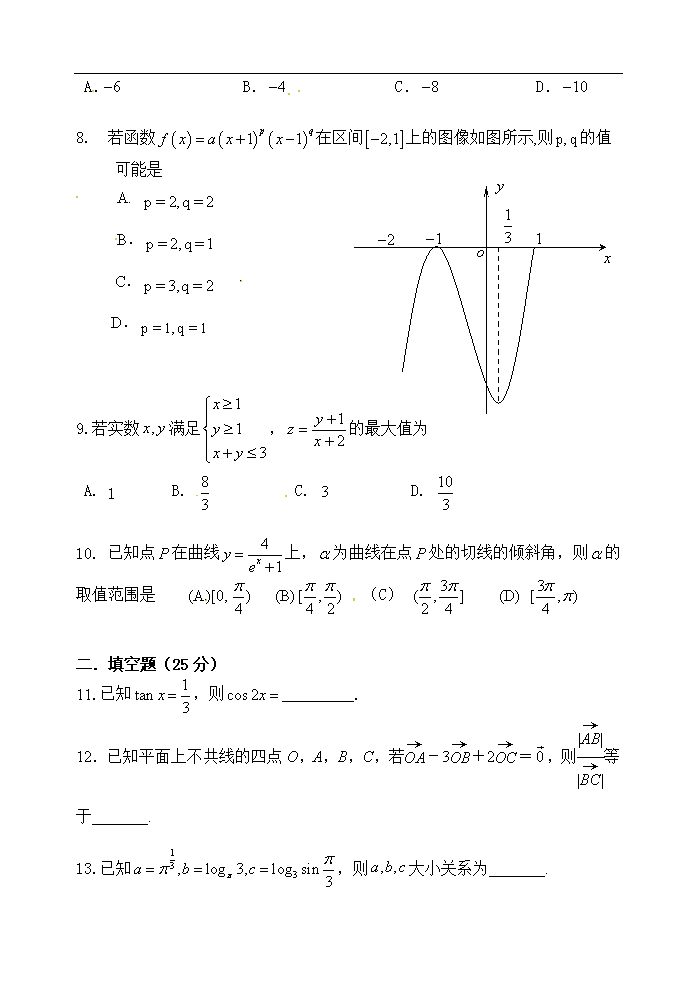

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
安徽省东至县2013届高三12月“一模”数学(文)试题
安徽省东至县2013届高三“一模”文科数学试卷 一.选择题(50分) 1.已知:集合P= {x| x≤3},则 A.-2P B.{-2}∈P C.{-2}P D.∈P 2.已知,则“”是“”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 3.已知向量,,,若∥,则= A.-5 B.5 C.-1 D.1 5 y y= -x+8 P x 0 4.如图,函数y=的图象在点P处的切线方程是y=-x+8, 则= A. B.1 C.2 D.0 5.函数对任意x∈R恒有f(x)≥0,则f(1)= A.3 B.4 C.5 D.6 6.将函数的图象向左平移个单位,再向上平移个单位,所得图象的解析式是 A. B. C. D. 7.已知等差数列的公差为,若成等比数列, 则 A. B. C. D. 8. 若函数在区间上的图像如图所示,则的值 可能是 A. B. C. D. 9.若实数满足,的最大值为 A. 1 B. C. D. 10. 已知点在曲线上,为曲线在点处的切线的倾斜角,则的取值范围是 (A)[0,) (B) (C) (D) 二.填空题(25分) 11.已知,则_________. 12.已知平面上不共线的四点O,A,B,C,若-3+2=,则等于_______. 13.已知,则大小关系为_______. 14.已知时, 则= . 15.如果对于函数f(x)定义域内任意的x,都有f(x)≥M(M为常数),称M为f(x)的下界,下界M中的最大值叫做f(x)的下确界,下列函数中,有下确界的所有函数是________. ①f(x)=sinx;②f(x)=lgx;③f(x)=ex;④f(x)=[来源:学_科_网] 三、解答题(75分) 16. (本小题满分12分)已知分别为三个内角的对边, (1)求; (2)若.的面积为,求[来源:学|科|网Z|X|X|K] 17. (本小题满分12分)设命题:函数是上的减函数,命题:函数在上的值域为,若“且”为假命题,“或”为真命题,求的取值范围. 18.(本小题满分12分) . [来源:学科网ZXXK] 19. (本小题满分13分)设函数f(x)=·b,其中向量=(2cosx,1),b=(cosx,sin2x+m). (1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间; (2)当x∈[0,] 时,f(x)的最大值为4,求m的值. 20.(本小题满分13分)某工厂生产一种产品的原材料费为每件40元,若用表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件元,又该厂职工工资固定支出12500元。 (1)把每件产品的成本费(元)表示成产品件数的函数,并求每件产品的最低成本费; (2)如果该厂生产的这种产品的数量不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价与产品件数有如下关系:,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本) 21.(本小题满分13分). 设函数 (1)将函数图象向右平移一个单位即可得到函数的图象,写出的解析式及值域; (2)关于x的不等式的解集中的整数恰有3个,求实数a的取值范围; [来源:学科网] 文科数学试卷答案 阅卷老师请注意:阅卷前请对答案进行审核 一.选择题(50分) 1 2 3 4 5 6 7 8 9 10 二.填空题(25分) 11. 12. 2 13. 14. 15. ①③④ 三、解答题(75分) 16. 解:(1)由及正弦定理得 . …………………………3分 由于,所以. 又,故. …………………………6分 (2) 的面积 而. …………………………10分 解得. …………………………12分 17. 解:由得, …………………3分 ∵在上的值域为,则…………6分 ∵“且”为假命题,“或”为真命题, ∴、为一真一假, 若真假,得, 若假真,得, 综上可知:的取值范围是或. ………………12分 . …………………………3分 …………………………6分 …………………………7分 ……10分 . …………………12分 19.解:(1)∵f(x)=a·b=2cos2x+sin2x+m=2sin(2x+)+m+1, ∴函数f(x)的最小正周期T==π. …………………………3分 在[0,π]上的单调递增区间为[0,],[,π]. ……………………8分 (2)当x∈[0,]时,∵f(x)单调递增, ……………………10分 ∴当x=时,f(x)取得最大值为m+3,即m+3=4.,解之得m=1 ∴m的值为1. …………13分 20.解:(Ⅰ) …………………………3分 由基本不等式得 ………………………5分 当且仅当,即时,等号成立.……………………6分 ∴,成本的最小值为90元.…………………7分 (Ⅱ)设总利润为元,则 …………………………11分 当时, 答:生产650件产品时,总利润最高,最高总利润为29750元.…………13分 21.解:(1)…………………………3分 值域为………………………5分 (2)解法一:不等式的解集中的整数恰有3个, 恰有三个整数解,故即………………8分 令 ………10分 所以函数 则另一个零点在区间 故解之得< …………13分 解法二:不等式的解集中的整数恰有3个,故即 ……………………8分[来源:学*科*网Z*X*X*K] 所以 …10分 所以—3解之得< …………13分查看更多