2020届广东省佛山市高三上学期第一次模拟考试数学理试题

2020届广东省佛山市高三上学期第一次模拟考试数学理试题

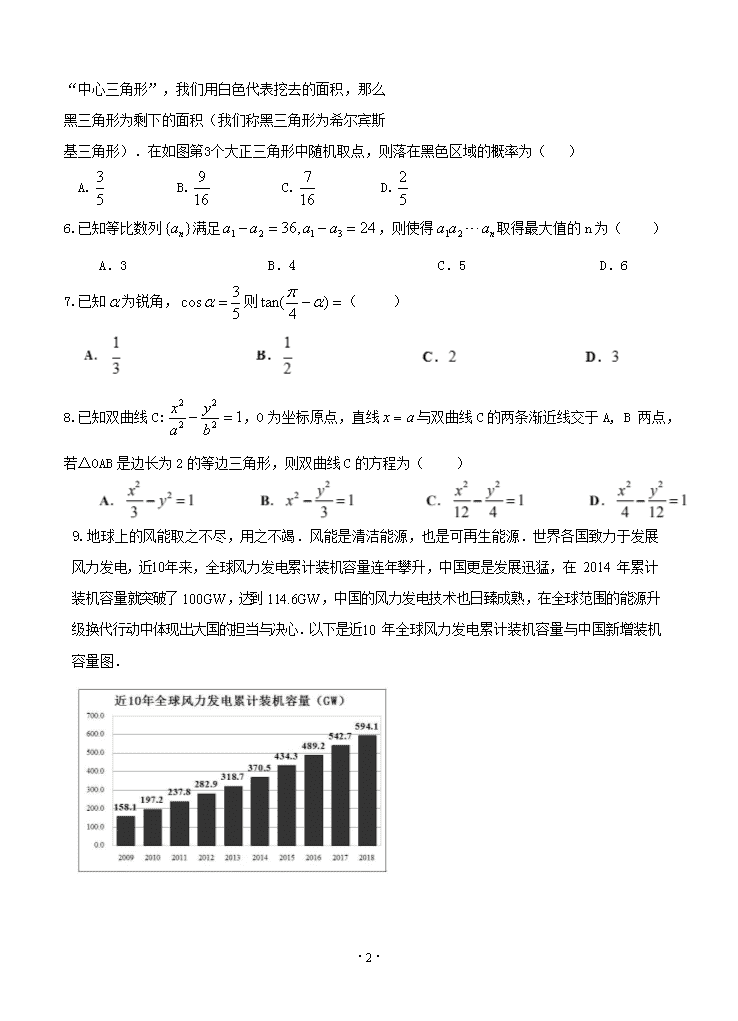
·1· 2019～2020 学年佛山市普通高中高三教学质量检测(一) 数 学(理科) 2020 年 1 月 7 日 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分 150 分．考试时间 120 分钟． 注意事项： 1. 答卷前，考生要务必填写答题卷上的有关项目． 2. 选择题每小题选出答案后，用 2B 铅笔把答案涂在答题卷相应的位置上． 3. 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内； 如需改动， 先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液，不按以上要求作答的 答案无效． 4. 请考生保持答题卷的整洁．考试结束后，将答题卷交回． 第Ⅰ卷(选择题 共 60 分) 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中， 只有一项是符合题目要求的． 1.在复平面内，复数 i i 21 5  对应的点位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 2.已知集合A x| x2  x 2 0 ，B x| | x |1，则A∩B  （ ） A．(2, 1) B．(1,1) C．(0,1) D．(1,2) 3.已知x, y R ，且x  y  0 ，则（ ） A. cos x cos y  0 B. cos x cos y  0 C．ln x  ln y  0 D．ln x  ln y  0 4.函数 f (x)的图像向左平移一个单位长度，所得图像与y  ex 关于y 轴对称，则 f (x)  （ ） A. 1xe B. 1xe C. 1xe D. 1xe 5.希尔宾斯基三角形是一种分形，由波兰数学家希尔宾斯基在 1915 年提出，先作一个正三角形， 挖去一个“中心三角形”（即以原三角形各边的中点为顶 ·2· 点的三角形），然后在剩下的小三角形中又挖去一个 “中心三角形”，我们用白色代表挖去的面积，那么 黑三角形为剩下的面积（我们称黑三角形为希尔宾斯 基三角形）．在如图第3个大正三角形中随机取点，则落在黑色区域的概率为（ ） A. 5 3 B. 16 9 C. 16 7 D. 5 2 6.已知等比数列 }{ na 满足 24,36 3121  aaaa ，则使得 naaa 21 取得最大值的 n 为（ ） A．3 B．4 C．5 D．6 7.已知 为锐角， 5 3cos  则  )4tan(  （ ） 8.已知双曲线 C: 12 2 2 2  b y a x ，O 为坐标原点，直线 ax  与双曲线 C 的两条渐近线交于 A, B 两点， 若△OAB 是边长为 2 的等边三角形，则双曲线 C 的方程为（ ） 9.地球上的风能取之不尽，用之不竭．风能是清洁能源，也是可再生能源．世界各国致力于发展 风力发电，近10年来，全球风力发电累计装机容量连年攀升，中国更是发展迅猛，在 2014 年累计 装机容量就突破了 100GW，达到 114.6GW，中国的风力发电技术也日臻成熟，在全球范围的能源升 级换代行动中体现出大国的担当与决心．以下是近 10 年全球风力发电累计装机容量与中国新增装 机容量图． ·3· 根据以上信息，正确的统计结论是（ ） A．截止到 2015 年中国累计装机容量达到峰值 B．10 年来全球新增装机容量连年攀升 C．10 年来中国新增装机容量平均超过 20GW D．截止到 2015 年中国累计装机容量在全球累计装机容量中占比超过 3 1 10.已知函数 1212 1)(  xxf x ，且 3)2()( 2  afaf ，则 a 的取值范围是（ ） 11.已知函数 f (x)  sin x  sin(πx)，现给出如下结论： ① f (x)是奇函数 ② f (x)是周期函数 ③ f (x)在区间(0, π) 上有三个零点 ④f (x) 的最大值为 2 其中正确结论的个数为（ ） A．1 B．2 C．3 D．4 12.已知正三棱柱 ABC  A1B1C1 的侧棱长为4 ，底面边长为 2 ，用一个平面截此棱柱，与侧棱 AA1 , BB1 ,CC1分别交于点 M , N , Q ，若△ MNQ 为直角三角形，则△ MNQ 面积的最大值为 （ ） 第Ⅱ卷(非选择题 共 90 分) 本卷包括必考题和选考题两部分．第 13～21 题为必考题，每个试题考生都必须作答．第 ·4· 22～23 为选考题，考生根据要求作答． 二、填空题：本大题共4小题，每小题5分，满分20分． 13.从进入决赛的6名选手中决出1名一等奖，2名二等奖，3名三等奖，则可能的决赛结果共有 种．（用数字作答） 14.在△ ABC 中， AB  2 ， AC  3 ， P 是边 BC 的垂直平分线上一点，则 AP  BC 。 函数 f (x)  ln x 和 g(x)  a 2x  x 的图象有公共点 P，且在点 P 处的切线相同，则这条切线 方程 为 . 16.在平面直角坐标系 xOy 中，对曲线 C 上任意一点 P ，P 到直线 x 1  0 的距离与该点到点 O 的距 离之和等于 2，则曲线 C 与 y 轴的交点坐标是 ；设点 A )0,4 5( ，则|PO|+|PA|的 最小值为 . 三、解答题：本大题共7小题，共70分，解答须写出必要的文字说明、证明过程或演算 步骤． 17.（本小题满分 12 分） 绿水青山就是金山银山．近年来，祖国各地依托本地自然资源，打造旅游产业，旅游业正蓬勃 发展。景区与游客都应树立尊重自然、顺应自然、保护自然的生态文明理念，合力使旅游市场走上 规范有序且可持续的发展轨道．某景区有一个自愿消费的项目：在参观某特色景点入口处会为每位 游客拍一张与景点的合影，参观后，在景点出口处会将刚拍下的照片打印出来，游客可自由选择是 否带走照片，若带走照片则需支付 20 元，没有被带走的照片会收集起来统一销毁。该项目运营一 段时间后，统计出平均只有三成的游客会选择带走照片．为改善运营状况，该项目组就照片收费与 游客消费意愿关系作了市场调研，发现收费与消费意愿有较强的线性相关性，并统计出在原有的基 础上，价格每下调 1 元，游客选择带走照片的可能性平均增加 0.05，假设平均每天约有 5000 人参 观该特色景点，每张照片的综合成本为 5 元，假设每个游客是否购买照片相互独立。 （1）若调整为支付 10 元就可带走照片，该项目每天的平均利润比调整前多还是少？ （2）要使每天的平均利润达到最大值，应如何定价？ 18.（本小题满分 12 分） ·5· 在△ABC 中，内角 A，B，C 的对边分别为 a，b，c，已知 a sin B  b sin )3( A . （1）求 A; （2）D 是线段 BC 上的点，若 AD  BD  2 ，CD  3 ，求△ADC 的面积. 19.（本小题满分 12 分） 已知椭圆 C : )0(12 2 2 2  bab y a x 的离心率为 2 1 ，点 A )2 3,1( 在椭圆 C 上，直线 1l 过椭 圆 C 的有交点与上顶点，动直线 kxyl :2 与椭圆 C 交于 M、N 两点，交 1l 于 P 点. （1）求椭圆 C 的方程； （2）已知 O 为坐标原点，若点 P 满足|OP|= 4 1 |MN|，求此时|MN|的长度. 20.（本小题满分 12 分） 如图，三棱锥 P  ABC 中，平面 PAB  平面 ABC ，PA  PB ，APB  ACB  90 ， 点 E, F 分别是棱 AB, PB 的中点，点 G 是△ BCE 的重心． （1）证明： GF / / 平面 PAC ； （2）若 GF 与平面 ABC 所成的角为60 ，求二面角BAPC的余弦值. 21.（本小题满分 12 分） 已知函数 f (x)  1  x  2 sin x, x  0 （1）求 f (x) 的最小值； ·6· （2）证明： xexf 2)(  . 请考生在第 22，23 题中任选一题做答，如果多做，则按所做的第一题计分，做答时请写清楚题号． 22．(本小题满分 10 分)[选修 4  4 :坐标系与参数方程选讲] 在直角坐标系 xOy 中，曲线 C 的参数方程为 m my mx ( 4 4 2      为参数） （1）写出曲线C的普通方程，并说明它表示什么曲线； （2）已知倾斜角互补的两条直线 21,ll ，其中 1l 与曲线C交于A，B两点， 2l 与C交于M，N两点， 1l 与 2l 交于点 ),( 00 yxP ，求证： |||||||| PNPMPBPA  . 23.（本小题满分 10 分）[选修 4-5：不等式选讲] 已知函数 |1|||)(  xaxxf . （1）若 2)( af ，求 a 的取值范围； （2）当 ],[ kaax  时，函数 )(xf 的值域为[1,3]，求k的值. ·7· ·8· ·9· ·10·