- 2021-06-16 发布 |
- 37.5 KB |
- 3页

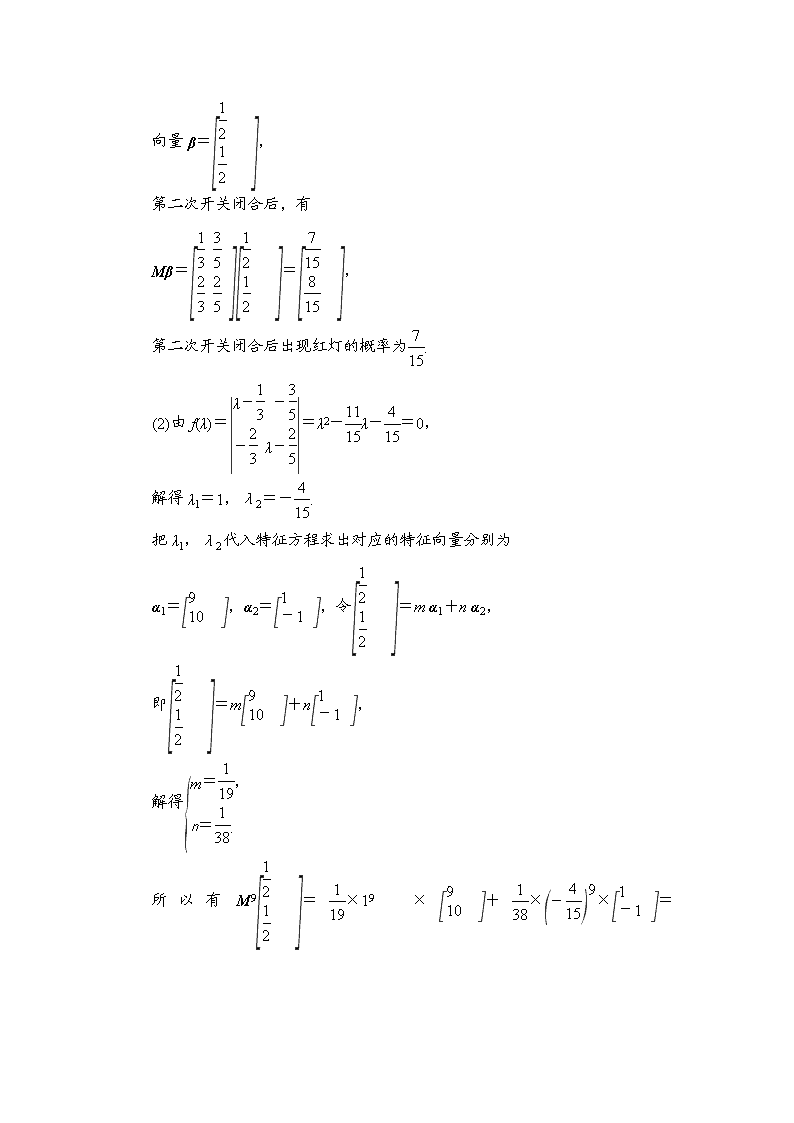

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习苏教版矩阵的应用章末分层突破学案
2019届一轮复习苏教版 矩阵的应用 章末分层突破 学案 转化与化归的思想 一个矩阵是一张由数据(或字母)排列成的表,它能把原本纷繁复杂的事物或数学对象的数学规律简单明了地表示出来,使人一目了然.同时,对矩阵施行某些运算,可以使我们看清事物之间或对象之间蕴涵的数学规律. 本章中广泛应用转化与化归思想,把实际问题转化为矩阵问题,然后通过矩阵变换加以解决. 某种电路开关闭合后,会出现红灯或绿灯闪动,已知开关第一次闭合后,出现红灯和出现绿灯的概率都是.从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是,出现绿灯的概率是;若前次出现绿灯,则下一次出现红灯的概率是,出现绿灯的概率是.问: (1)第二次闭合后出现红灯的概率是多少? (2)开关闭合10次时,出现绿灯的概率是多少? 【导学号:30650061】 【解】 (1)从第二次开关闭合后,红绿灯变化的概率情况如图所示: 根据图写出红绿灯变化的转移矩阵, 即M=. 第一次闭合开关后出现红灯和绿灯的概率可表示为 向量β=, 第二次开关闭合后,有 Mβ==, 第二次开关闭合后出现红灯的概率为. (2)由f(λ)==λ2-λ-=0, 解得λ1=1,λ2=-. 把λ1,λ2代入特征方程求出对应的特征向量分别为 α1=,α2=,令=m α1+n α2, 即=m+n, 解得 所以有M9=×19×+××=≈ . 所以开关闭合10次时, 出现绿灯的概率约为.查看更多