数学卷·2018届四川省成都市温江区高二上学期期末数学试卷（理科） （解析版）

数学卷·2018届四川省成都市温江区高二上学期期末数学试卷（理科） （解析版）

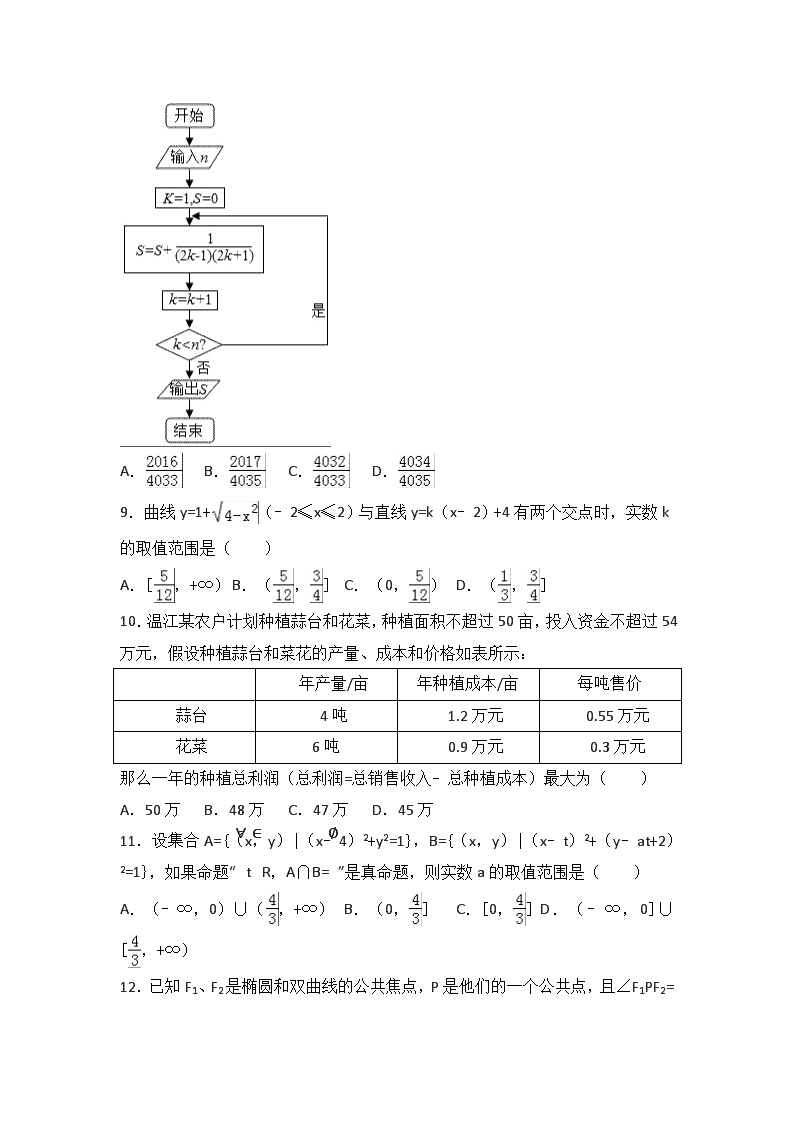
‎2016-2017学年四川省成都市温江区高二（上）期末数学试卷（理科）‎ ‎　‎ 一、选择题 ‎1．过点M（﹣3，2），N（﹣2，3）的直线倾斜角是（　　）‎ A． B． C． D．‎ ‎2．如图是2016年某学生进行舞蹈比赛环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分，所剩数据的平均数和众数依次是（　　）‎ A．85.84 B．84.85 C．85.87 D．84.86‎ ‎3．抛物线x2=4y的准线方程是（　　）‎ A．y=﹣1 B．y=﹣2 C．x=﹣1 D．x=﹣2‎ ‎4．已知命题p：∀x＞0，x3＞0，那么￢p是（　　）‎ A．∀x＞0，x3≤0 B．‎ C．∀x＜0，x3≤0 D．‎ ‎5．实验测得五组（x，y）的值是（1，2）（2，4）（3，4）（4，7）（5，8），若线性回归方程为=0.7x+，则的值是（　　）‎ A．1.4 B．1.9 C．2.2 D．2.9‎ ‎6．“a≤2”是“方程x2+y2﹣2x+2y+a=0表示圆”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎7．两直线3x+y﹣3=0与3x+my+=0平行，则它们之间的距离是（　　）‎ A．4 B． C． D． ‎ ‎8．阅读如图所示的程序框图，若输入n=2017，则输出的S值是（　　）‎ A． B． C． D．‎ ‎9．曲线y=1+（﹣2≤x≤2）与直线y=k（x﹣2）+4有两个交点时，实数k的取值范围是（　　）‎ A．[，+∞） B．（，] C．（0，） D．（，]‎ ‎10．温江某农户计划种植蒜台和花菜，种植面积不超过50亩，投入资金不超过54万元，假设种植蒜台和菜花的产量、成本和价格如表所示：‎ ‎　年产量/亩 年种植成本/亩　‎ 每吨售价　‎ ‎　蒜台 ‎　4吨 ‎　1.2万元 ‎　0.55万元 ‎　花菜 ‎6吨　‎ ‎　0.9万元 ‎　0.3万元 那么一年的种植总利润（总利润=总销售收入﹣总种植成本）最大为（　　）‎ A．50万 B．48万 C．47万 D．45万 ‎11．设集合A={（x，y）|（x﹣4）2+y2=1}，B={（x，y）|（x﹣t）2+（y﹣at+2）2=1}，如果命题“∀t∈R，A∩B=∅”是真命题，则实数a的取值范围是（　　）‎ A．（﹣∞，0）∪（，+∞） B．（0，] C．[0，] D．（﹣∞，0]∪[，+∞）‎ ‎12．已知F1、F2是椭圆和双曲线的公共焦点，P是他们的一个公共点，且∠F1PF2=‎ ‎，则椭圆和双曲线的离心率之积的最小值为（　　）‎ A． B． C． D．1‎ ‎　‎ 二、填空题 ‎13．空间中点A（2，3，5）与B（3，1，4），则|AB|=　　．‎ ‎14．某单位在岗职工624人，为了调查工人用于上班途中的时间，决定采用系统抽样方法抽取10%的工人进行调查，首先在总体中随机剔除4人，将剩下的620名职工编号（分别为000，001，002，…，619），若样本中的最小编号是007，则样本中的最大编号是　　．‎ ‎15．已知抛物线y2=2px（p＞0）上一点M（1，m）（m＞0）到其焦点的距离为5，双曲线﹣y2=1的左顶点为A．若双曲线的一条渐近线与直线AM平行，则实数a等于　　．‎ ‎16．给出下列结论：‎ 动点M（x，y）分别到两定点（﹣4，0），（4，0）连线的斜率之乘积为﹣，设M（x，y）的轨迹为曲线C，F1、F2分别为曲线C的左右焦点，则下列命题中：‎ ‎（1）曲线C的焦点坐标为F1（﹣5，0），F2（5，0）；‎ ‎（2）曲线C上存在一点M，使得S△F1MF2=9；‎ ‎（3）P为曲线C上一点，P，F1，F2是直角三角形的三个顶点，且|PF1|＞|PF2|，的值为；‎ ‎（4）设A（1，1），动点P在曲线C上，则|PA|+|PF1|的最大值为8+；‎ 其中正确命题的序号是　　．‎ ‎　‎ 三、解答题 ‎17．（10分）已知△ABC的三个顶点坐标分别为A（8，5），B（4，﹣2），C（﹣6，3）．‎ ‎（1）求AC边上的中线所在直线方程；‎ ‎（2）求AB边上的高所在直线方程．‎ ‎18．（10分）从参加高二年级期中考试的学生中随机抽取60名学生，将其英语成绩分成六段[40，50），[50，60），…，[90，100）后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：‎ ‎（1）求分数在[70，80）内的频率，并补全这个频率分布直方图；‎ ‎（2）根据补充完整频率分布直方图估计出本次考试的平均分数、中位数；（小数点后保留一位有效数字）‎ ‎（3）用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本，则各分数段抽取的人数分别是多少？‎ ‎19．（12分）p：实数x满足x2﹣4ax+3a2＜0，其中a＞0，q：实数x满足 ‎（1）若a=1，且p∧q为真，求实数x的取值范围；‎ ‎（2）¬p是¬q的充分不必要条件，求实数a的取值范围．‎ ‎20．（12分）某公司2017年元旦晚会现场，为了活跃气氛，将在晚会节目表演过程中进行抽奖活动．‎ ‎（1）现需要从第一排就座的6位嘉宾A、B、C、D、E、F中随机抽取2人上台抽奖，求嘉宾A和嘉宾B至少有一人上台抽奖的概率；‎ ‎（2）抽奖活动的规则是：嘉宾通过操作按键使电脑自动产生两个[0，1]之间的随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该嘉宾中奖；若电脑显示“谢谢”，则不中奖．求该嘉宾中奖的概率．‎ ‎21．（12分）已知圆F的圆心坐标为（1，0），且被直线x+y﹣2=0截得的弦长为．‎ ‎（1）求圆F的方程；‎ ‎（2）若动圆M与圆F相外切，又与y轴相切，求动圆圆心M的轨迹方程；‎ ‎（3）直线l与圆心M轨迹位于y轴右侧的部分相交于A、B两点，且•=﹣4，证明直线l必过一定点，并求出该定点．‎ ‎22．（14分）以椭圆C： +=1（a＞b＞0）的中心O为圆心，以为半径的圆称为该椭圆的“伴随”．‎ ‎（1）若椭圆C的离心率为，其“伴随”与直线x+y﹣2=0相切，求椭圆C的方程．‎ ‎（2）设椭圆E： +=1，P为椭圆C上任意一点，过点P的直线y=kx+m交椭圆E于AB两点，射线PO交椭圆E于点Q．‎ ‎（i）求的值；‎ ‎（ii）求△ABQ面积的最大值．‎ ‎　‎ ‎2016-2017学年四川省成都市温江区高二（上）期末数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．过点M（﹣3，2），N（﹣2，3）的直线倾斜角是（　　）‎ A． B． C． D．‎ ‎【考点】直线的倾斜角．‎ ‎【分析】设直线倾斜角为θ，θ∈[0，π）．利用斜率计算公式可得tanθ=1，即可得出．‎ ‎【解答】解：设直线倾斜角为θ，θ∈[0，π）．‎ 则tanθ==1，∴θ=．‎ 故选：B．‎ ‎【点评】本题考查了直线倾斜角与斜率的计算公式，考查了推理能力与计算能力，属于基础题．‎ ‎　‎ ‎2．如图是2016年某学生进行舞蹈比赛环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分，所剩数据的平均数和众数依次是（　　）‎ A．85.84 B．84.85 C．85.87 D．84.86‎ ‎【考点】众数、中位数、平均数．‎ ‎【分析】去掉一个最高分和一个最低分，所剩数据为84，84，86，84，87，由此能求出所剩数据的平均数和众数．‎ ‎【解答】解：去掉一个最高分和一个最低分，‎ 所剩数据为84，84，86，84，87，‎ ‎∴所剩数据的平均数为：‎ ‎=（84+84+86+84+87）=85，‎ 所剩数据众数为：84．‎ 故选：A．‎ ‎【点评】本题考查所剩数据的平均数和众数的求法，是基础题，解题时要认真审题，注意茎叶力图的合理运用．‎ ‎　‎ ‎3．抛物线x2=4y的准线方程是（　　）‎ A．y=﹣1 B．y=﹣2 C．x=﹣1 D．x=﹣2‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】由x2=2py（p＞0）的准线方程为y=﹣，则抛物线x2=4y的准线方程即可得到．‎ ‎【解答】解：由x2=2py（p＞0）的准线方程为y=﹣，‎ 则抛物线x2=4y的准线方程是y=﹣1，‎ 故选A．‎ ‎【点评】本题考查抛物线的方程和性质，主要考查抛物线的准线方程的求法，属于基础题．‎ ‎　‎ ‎4．已知命题p：∀x＞0，x3＞0，那么￢p是（　　）‎ A．∀x＞0，x3≤0 B．‎ C．∀x＜0，x3≤0 D．‎ ‎【考点】命题的否定．‎ ‎【分析】利用全称命题的否定是特称命题，写出结果即可．‎ ‎【解答】解：因为全称命题的否定是特称命题，所以，命题p：∀x＞0，x3＞0，那么￢p是．‎ 故选：D．‎ ‎【点评】本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．‎ ‎　‎ ‎5．实验测得五组（x，y）的值是（1，2）（2，4）（3，4）（4，7）（5，8），若线性回归方程为=0.7x+，则的值是（　　）‎ A．1.4 B．1.9 C．2.2 D．2.9‎ ‎【考点】线性回归方程．‎ ‎【分析】根据五组（x，y）的值计算、，利用线性回归方程过样本中心点求出的值．‎ ‎【解答】解：根据五组（x，y）的值，计算 ‎=×（1+2+3+4+5）=3，‎ ‎=×（2+4+4+7+8）=5，‎ 且线性回归方程=0.7x+过样本中心点，‎ 则=﹣0.7=5﹣0.7×3=2.9．‎ 故选：D．‎ ‎【点评】本题考查了平均数与线性回归方程过样本中心点的应用问题，是基础题目．‎ ‎　‎ ‎6．“a≤2”是“方程x2+y2﹣2x+2y+a=0表示圆”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【考点】圆的一般方程．‎ ‎【分析】方程x2+y2﹣2x+2y+a=0表示圆，则4+4﹣4a＞0，可得a＜2，即可得出结论．‎ ‎【解答】解：方程x2+y2﹣2x+2y+a=0表示圆，则4+4﹣4a＞0，∴a＜2，‎ ‎∵“a≤2”是a＜2的必要不充分条件，‎ ‎∴“a≤2”是“方程x2+y2﹣2x+2y+a=0表示圆”的必要不充分条件，‎ 故选B．‎ ‎【点评】本题考查圆的方程，考查充要条件的判断，比较基础．‎ ‎　‎ ‎7．两直线3x+y﹣3=0与3x+my+=0平行，则它们之间的距离是（　　）‎ A．4 B． C． D． ‎ ‎【考点】两条平行直线间的距离．‎ ‎【分析】根据两条直线平行的条件，解出m=1，利用两条平行直线间的距离公式加以计算，可得答案．‎ ‎【解答】解：∵直线3x+y﹣3=0与3x+my+=0平行，‎ ‎∴m=1．‎ 因此，直线3x+y﹣3=0与3x+y+=0之间的距离为d==，‎ 故选：D．‎ ‎【点评】本题已知两条直线互相平行，求参数m的值并求两条直线的距离．着重考查了直线的位置关系、平行线之间的距离公式等知识，属于基础题．‎ ‎　‎ ‎8．阅读如图所示的程序框图，若输入n=2017，则输出的S值是（　　）‎ A． B． C． D．‎ ‎【考点】程序框图．‎ ‎【分析】根据程序框图的流程，依次写出每次循环得到的S，k的值，当k=2017时，不满足条件k＜2017，退出循环，输出S的值，用裂项相消法求和即可得解．‎ ‎【解答】解：模拟程序的运行，可得：‎ n=2017，k=1，S=0‎ 执行循环体，S=0+，k=2；‎ 满足条件k＜2017，执行循环体，S=0++，k=3；‎ ‎…‎ 满足条件k＜2017，执行循环体，S=0+++…+，k=2017；‎ 此时，不满足条件k＜2017，退出循环，输出S的值．‎ 由于：S=0+++…+=×[（1﹣）+（）+…+（﹣）]=（1﹣）=．‎ 故选：A．‎ ‎【点评】本题考查了直到型循环结构的程序框图，由程序框图判断程序运行的功能，用裂项相消法求和是解答本题的关键，属于基础题．‎ ‎　‎ ‎9．曲线y=1+（﹣2≤x≤2）与直线y=k（x﹣2）+4有两个交点时，实数k的取值范围是（　　）‎ A．[，+∞） B．（，] C．（0，） D．（，]‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】先确定曲线的性质，然后结合图形确定临界状态，结合直线与圆相交的性质，可解得k的取值范围．‎ ‎【解答】解：y=1+可化为x2+（y﹣1）2=4，y≥1，所以曲线为以（0，1）为圆心，2为半径的圆y≥1的部分．‎ 直线y=k（x﹣2）+4过定点p（2，4），由图知，当直线经过A（﹣2，1）点时恰与曲线有两个交点，顺时针旋转到与曲线相切时交点边为一个．‎ 且kAP==，由直线与圆相切得d==2，解得k=，‎ 则实数k的取值范围为，‎ 故选B．‎ ‎【点评】本题考查直线与圆相交的性质，同时考查了学生数形结合的能力，注意函数的定义域，以及斜率范围的确定，可以采用估计法解答．‎ ‎　‎ ‎10．温江某农户计划种植蒜台和花菜，种植面积不超过50亩，投入资金不超过54万元，假设种植蒜台和菜花的产量、成本和价格如表所示：‎ ‎　年产量/亩 年种植成本/亩　‎ 每吨售价　‎ ‎　蒜台 ‎　4吨 ‎　1.2万元 ‎　0.55万元 ‎　花菜 ‎6吨　‎ ‎　0.9万元 ‎　0.3万元 那么一年的种植总利润（总利润=总销售收入﹣总种植成本）最大为（　　）‎ A．50万 B．48万 C．47万 D．45万 ‎【考点】简单线性规划．‎ ‎【分析】由题意，设农户计划种植蒜台和花菜分别x亩，y亩；从而可得约束条件以及目标函数总利润z=0.55×4x+0.3×6y﹣（1.2x+0.9y）=x+0.9y；从而由线性规划求最优解即可 ‎【解答】解：设农户计划种植蒜台和花菜各x亩，y亩；‎ 则由题意可得，；‎ 一年的种植总利润z=0.55×4x+0.3×6y﹣（1.2x+0.9y）=x+0.9y；‎ 作平面区域如下，‎ 结合图象可知，‎ ‎；‎ 解得x=30，y=20；此时一年的种植总利润最大为30+0.9×20=48；‎ 故选：B．‎ ‎【点评】本题考查了线性规划在实际问题中的应用及学生的作图能力，关键是正确列出约束条件以及目标函数，利用简单线性规划解决最优解问题；属于中档题．‎ ‎　‎ ‎11．设集合A={（x，y）|（x﹣4）2+y2=1}，B={（x，y）|（x﹣t）2+（y﹣at+2）2=1}，如果命题“∀t∈R，A∩B=∅”是真命题，则实数a的取值范围是（　　）‎ A．（﹣∞，0）∪（，+∞） B．（0，] C．[0，] D．（﹣∞，0]∪[，+∞）‎ ‎【考点】交集及其运算．‎ ‎【分析】集合A、B分别表示两个圆：圆心M（4，0），r1=1和圆心N（t，at﹣2），r2=1，且两圆一定有公共点，从而得到（a2+1）t2﹣（8+4a）t+16≤0．由此能求出实数a的取值范围．‎ ‎【解答】解：∵集合A、B分别表示两个圆，‎ 圆心M（4，0），r1=1，‎ N（t，at﹣2），r2=1，‎ ‎∃t∈R，A∩B≠∅，则两圆一定有公共点，‎ ‎|MN|=，0≤|MN|≤2，‎ 即|MN|2≤4，化简得，（a2+1）t2﹣（8+4a）t+16≤0．‎ ‎∵a2+1＞0，‎ ‎∴△=（8+4a）2﹣4（a2+1）×16≥0，‎ 即3a2﹣4a≤0，‎ ‎∴0≤a≤．‎ 故选：C．‎ ‎【点评】本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意圆的性质的合理运用．‎ ‎　‎ ‎12．已知F1、F2是椭圆和双曲线的公共焦点，P是他们的一个公共点，且∠F1PF2=，则椭圆和双曲线的离心率之积的最小值为（　　）‎ A． B． C． D．1‎ ‎【考点】椭圆的简单性质；双曲线的简单性质．‎ ‎【分析】先设椭圆的长半轴长为a1，双曲线的半实轴长a2，焦距2c．因为涉及椭圆及双曲线离心率的问题，所以需要找a1，a2，c之间的关系，而根据椭圆及双曲线的定义可以用a1，a2表示出|PF1|，|PF2|，在△F1PF2中根据余弦定理可得到，利用基本不等式可得结论．‎ ‎【解答】解：如图，设椭圆的长半轴长为a1，双曲线的半实轴长为a2，则根据椭圆及双曲线的定义：‎ ‎|PF1|+|PF2|=2a1，|PF1|﹣|PF2|=2a2，‎ ‎∴|PF1|=a1+a2，|PF2|=a1﹣a2，‎ 设|F1F2|=2c，∠F1PF2=，则：‎ 在△PF1F2中由余弦定理得，‎ ‎4c2=（a1+a2）2+（a1﹣a2）2﹣2（a1+a2）（a1﹣a2）cos ‎∴化简得：a12+3a22=4c2‎ ‎，又因为，∴e1e2≥，‎ 故选：C ‎【点评】本题考查圆锥曲线的共同特征，考查通过椭圆与双曲线的定义求焦点三角形三边长，解决本题的关键是根据所得出的条件灵活变形，求出焦点三角形的边长来，属于难题．‎ ‎　‎ 二、填空题 ‎13．空间中点A（2，3，5）与B（3，1，4），则|AB|=　　．‎ ‎【考点】空间两点间的距离公式．‎ ‎【分析】直接利用空间两点间的距离公式求解即可．‎ ‎【解答】解：∵A（2，3，5），B（3，1，4），‎ ‎∴|AB|==，‎ 故答案为．‎ ‎【点评】本题考查空间两点间的距离公式的运用，考查学生的计算能力，比较基础．‎ ‎　‎ ‎14．某单位在岗职工624人，为了调查工人用于上班途中的时间，决定采用系统抽样方法抽取10%的工人进行调查，首先在总体中随机剔除4人，将剩下的620名职工编号（分别为000，001，002，…，619），若样本中的最小编号是007，则样本中的最大编号是　617　．‎ ‎【考点】系统抽样方法．‎ ‎【分析】根据系统抽样的定义，求出组距和组数即可得到结论 ‎【解答】解：第一步：将624名职工用随机方式进行编号，‎ 第二步：从总体中剔除4人（剔除方法可用随机数法），将剩下的620名职工重新编号，分别为000，001，002，…，619，并分成62段，‎ 第三步：在第一段000，001，002，…，009这十个编号中用简单随机抽样确定起始号码007，‎ 第四步：将编号为7，7+10，7+20，i 0+20，…，7+610=617的个体抽出，组成样本．‎ 故样本中的最大编号是617，‎ 故答案为：617．‎ ‎【点评】本题主要考查系统抽样的应用，根据条件求出组距是解决本题的关键，比较基础．‎ ‎　‎ ‎15．已知抛物线y2=2px（p＞0）上一点M（1，m）（m＞0）到其焦点的距离为5，双曲线﹣y2=1的左顶点为A．若双曲线的一条渐近线与直线AM平行，则实数a等于　　．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】设M点到抛物线准线的距离为d，由已知可得p值，由双曲线的一条渐近线与直线AM平行，可得，解得实数a的值．‎ ‎【解答】解：设M点到抛物线准线的距离为d，‎ 则⇒p=8，‎ 所以抛物线方程为y2=16x，M的坐标为（1，4）；‎ 又双曲线的左顶点为，‎ 渐近线为，‎ 所以，由题设可得，‎ 解得．‎ 故答案为：‎ ‎【点评】本题考查的知识点是抛物线的简单性质，双曲线的简单性质，是抛物线与双曲线的综合应用，难度中档．‎ ‎　‎ ‎16．给出下列结论：‎ 动点M（x，y）分别到两定点（﹣4，0），（4，0）连线的斜率之乘积为﹣，设M（x，y）的轨迹为曲线C，F1、F2分别为曲线C的左右焦点，则下列命题中：‎ ‎（1）曲线C的焦点坐标为F1（﹣5，0），F2（5，0）；‎ ‎（2）曲线C上存在一点M，使得S△F1MF2=9；‎ ‎（3）P为曲线C上一点，P，F1，F2是直角三角形的三个顶点，且|PF1|＞|PF2|，的值为；‎ ‎（4）设A（1，1），动点P在曲线C上，则|PA|+|PF1|的最大值为8+；‎ 其中正确命题的序号是　③④　．‎ ‎【考点】直线与椭圆的位置关系．‎ ‎【分析】设M（x，y），由题意可得kMA•kMB=﹣，运用直线的斜率公式，化简即可得到点P的轨迹为曲线C是以F1（﹣，0），F2（，0）为焦点的椭圆，根据椭圆的性质可逐一判定．‎ ‎【解答】解：设M（x，y），则kMA•kMB=，化简得 曲线C是以F1（﹣，0），F2（，0）为焦点的椭圆，‎ 对于（1），曲线C的焦点坐标为F1（﹣5，0），F2（5，0）错；‎ 对于（2），因为b2=9，要使S△F1MF2=9，必须要存在点M，使∠F1MF2=900‎ ‎∵c==3，∴不存在M，使得S△F1MF2=9，故错；‎ 对于（3），由（2）得，P为曲线C上一点，P，F1，F2是直角三角形的三个顶点，‎ 且|PF1|＞|PF2|，则必有PF1⊥F1F2‎ ‎|PF1|=，|PF2|=2a﹣|PF1|=，∴的值为，正确；‎ 对于（4），则|PA|+|PF1|=2a+|PA|﹣|PF2|≤2a+|PA|=8+，故正确；‎ 故答案为：③④‎ ‎【点评】本题考查了椭圆的方程及性质，结合平面几何的知识是关键，属于难题．‎ ‎　‎ 三、解答题 ‎17．（10分）（2016秋•温江区期末）已知△ABC的三个顶点坐标分别为A（8，5），B（4，﹣2），C（﹣6，3）．‎ ‎（1）求AC边上的中线所在直线方程；‎ ‎（2）求AB边上的高所在直线方程．‎ ‎【考点】待定系数法求直线方程．‎ ‎【分析】（1）线段AC的中点D坐标为（1，4），利用两点式方程能求出AC边上的中线所在的直线方程；‎ ‎（2），AB边上高的斜率是﹣，且过点C（﹣6，3），由此能求出AB边上的高所在的直线方程．‎ ‎【解答】解：（1）线段AC的中点D坐标为（1，4）‎ AC边上的中线BD所在直线的方程是：，即2x+y﹣6=0；‎ ‎（2），AB边上高的斜率是﹣，‎ AB边上的高所在直线方程是y﹣3=（x+6），即4x+7y+3=0．‎ ‎【点评】本题主要考查直线的斜率公式、用点斜式求直线的方程，属于基础题．‎ ‎　‎ ‎18．（10分）（2016秋•温江区期末）从参加高二年级期中考试的学生中随机抽取60名学生，将其英语成绩分成六段[40，50），[50，60），…，[90，100）后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：‎ ‎（1）求分数在[70，80）内的频率，并补全这个频率分布直方图；‎ ‎（2）根据补充完整频率分布直方图估计出本次考试的平均分数、中位数；（小数点后保留一位有效数字）‎ ‎（3）用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本，则各分数段抽取的人数分别是多少？‎ ‎【考点】频率分布直方图；分层抽样方法．‎ ‎【分析】（1）计算分数在[70，80）内的频率，利用求出小矩形的高，补出图形即可；‎ ‎（2）根据频率分布直方图，计算平均分与中位数即可；‎ ‎（3）根据分层抽样原理，计算各分数段内应抽取的人数即可．‎ ‎【解答】解：（1）分数在[70，80）内的频率为 ‎1﹣（0.010+0.015+0.015+0.025+0.005）×10=1﹣0.7=0.3．‎ 又=0.03，补出的图形如下图所示；‎ ‎（2）根据频率分布直方图，计算平均分为：‎ ‎=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71，‎ 估计这次考试的平均分是71；‎ 又0.01×10+0.015×10+0.015×10=0.4＜0.5，‎ ‎0.4+0.03×10=0.7＞0.5，‎ ‎∴中位数在[70，80）内，‎ 计算中位数为70+≈73.3；‎ ‎（3）根据分层抽样原理，[40，50）分数段应抽取人数为0.10×20=2人；‎ ‎[50，60）分数段应抽取人数为0.15×20=3人；‎ ‎[60，70）分数段应抽取人数为0.15×20=3人；‎ ‎[70，80）分数段应抽取人数为0.3×20=6人；‎ ‎[80，90）分数段应抽取人数为0.25×20=5人；‎ ‎[90，100]分数段应抽取人数为0.05×20=1人．‎ ‎【点评】本题主要考查了频率分布直方图以及平均数、中位数的计算问题，也考查了分层抽样原理的运用问题，是基础题目．‎ ‎　‎ ‎19．（12分）（2016秋•温江区期末）p：实数x满足x2﹣4ax+3a2＜0，其中a＞0，q：实数x满足 ‎（1）若a=1，且p∧q为真，求实数x的取值范围；‎ ‎（2）¬p是¬q的充分不必要条件，求实数a的取值范围．‎ ‎【考点】必要条件、充分条件与充要条件的判断；复合命题的真假．‎ ‎【分析】（1）若a=1，分别求出p，q成立的等价条件，利用且p∧q为真，求实数x的取值范围；‎ ‎（2）利用￢p是￢q的充分不必要条件，即q是p的充分不必要条件，求实数a的取值范围．‎ ‎【解答】解：（1）由x2﹣4ax+3a2＜0，得（x﹣3a）（x﹣a）＜0．又a＞0，‎ 所以a＜x＜3a．‎ 当a=1时，1＜x＜3，即p为真时实数x的取值范围是1＜x＜3．‎ 由得 得2＜x≤3，‎ 即q为真时实数x的取值范围是2＜x≤3．‎ 若p∧q为真，则p真且q真，‎ 所以实数x的取值范围是2＜x＜3．‎ ‎（2）￢p是￢q的充分不必要条件，即￢p⇒￢q，且￢q推不出￢p．‎ 即q是p的充分不必要条件，‎ 则，解得1＜a≤2，‎ 所以实数a的取值范围是1＜a≤2．‎ ‎【点评】本题主要考查复合命题与简单命题之间的关系，利用逆否命题的等价性将￢p是￢q的充分不必要条件，转化为q是p的充分不必要条件是解决本题的关键，‎ ‎　‎ ‎20．（12分）（2016秋•温江区期末）某公司2017年元旦晚会现场，为了活跃气氛，将在晚会节目表演过程中进行抽奖活动．‎ ‎（1）现需要从第一排就座的6位嘉宾A、B、C、D、E、F中随机抽取2人上台抽奖，求嘉宾A和嘉宾B至少有一人上台抽奖的概率；‎ ‎（2）抽奖活动的规则是：嘉宾通过操作按键使电脑自动产生两个[0，1]之间的随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该嘉宾中奖；若电脑显示“谢谢”，则不中奖．求该嘉宾中奖的概率．‎ ‎【考点】程序框图；列举法计算基本事件数及事件发生的概率．‎ ‎【分析】（1）根据古典概型的概率公式，可得A和B至少有一人上台抽奖的概率；‎ ‎（2）确定满足0≤x≤1，0≤y≤1点的区域，由条件，到的区域为图中的阴影部分，计算面积，可求该代表中奖的概率．‎ ‎【解答】‎ 解：（1）6位嘉宾，从中抽取2人上台抽奖的基本事件有（a，b），（a，c），（a，d），（a，e），（a，f），（b，c），（b，d），（b，e），（b．f），（c，d），（c，e），（c，f），（d，e），（d，f），（e，f）共15种，其中a和b至少有一人上台抽奖的基本事件有9种，‎ ‎∴a和b至少有一人上台抽奖的概率为=；‎ ‎（2）由已知0≤x≤1，0≤y≤1，点（x，y）在如图所示的正方形OABC内，‎ 由条件，得到的区域为图中的阴影部分，‎ 由2x﹣y﹣1=0，令y=0，可得x=，令y=1，可得x=1，‎ ‎∴在x，y∈[0，1]时满足2x﹣y﹣1≤0的区域的面积为S阴=（1+）×1=．‎ ‎∴该代表中奖的概率为=．‎ ‎【点评】本题考查概率与统计知识，考查分层抽样，考查概率的计算，确定概率的类型是关键，属于基础题．‎ ‎　‎ ‎21．（12分）（2016秋•温江区期末）已知圆F的圆心坐标为（1，0），且被直线x+y﹣2=0截得的弦长为．‎ ‎（1）求圆F的方程；‎ ‎（2）若动圆M与圆F相外切，又与y轴相切，求动圆圆心M的轨迹方程；‎ ‎（3）直线l与圆心M轨迹位于y轴右侧的部分相交于A、B两点，且•=﹣4，证明直线l必过一定点，并求出该定点．‎ ‎【考点】直线和圆的方程的应用．‎ ‎【分析】（1）设圆F的方程为（x﹣1）2+y2=r2，r＞0，运用弦长公式和点到直线的距离公式，即可得到半径r，可得圆F的方程；‎ ‎（2）由题意可得M到点F的距离比它到y轴的距离大1，即为M到点F的距离比它到直线x=﹣1的距离相等，由抛物线的定义可得抛物线的方程；‎ ‎（3）设出直线的方程，同抛物线方程联立，得到关于y的一元二次方程，根据根与系数的关系表示出数量积，根据数量积等于﹣4，做出数量积表示式中的b的值，即得到定点的坐标．‎ ‎【解答】解：（1）设圆F的方程为（x﹣1）2+y2=r2，r＞0，‎ 由圆心到直线x+y﹣2=0的距离为d==，‎ 由弦长公式可得=2，解得r=1，‎ 可得圆F的方程为（x﹣1）2+y2=1；‎ ‎（2）设M的坐标为（x，y），由动圆M与圆F相外切，又与y轴相切，‎ 可得M到点F的距离比它到y轴的距离大1，‎ 即为M到点F的距离比它到直线x=﹣1的距离相等，‎ 由抛物线的定义，可得动圆圆心M的轨迹方程为y2=4x；‎ ‎（3）证明：设l：x=ty+b代入抛物线y2=4x，消去x得 y2﹣4ty﹣4b=0设A（x1，y1），B（x2，y2）‎ 则y1+y2=4t，y1y2=﹣4b，‎ ‎∴•=x1x2+y1y2=（ty1+b）（ty2+b）+y1y2‎ ‎=t2y1y2+bt（y1+y2）+b2+y1y2‎ ‎=﹣4bt2+4bt2+b2﹣4b=b2﹣4b 令b2﹣4b=﹣4，∴b2﹣4b+4=0∴b=2．‎ ‎∴直线l过定点（2，0）．‎ ‎【点评】本题考查圆的方程的求法，注意运用待定系数法和定义法，考查直线方程和抛物线方程联立，运用韦达定理，考查方程思想和向量数量积的坐标表示，考查运算能力，属于中档题．‎ ‎　‎ ‎22．（14分）（2016秋•温江区期末）以椭圆C： +=1（a＞b＞0）的中心O为圆心，以为半径的圆称为该椭圆的“伴随”．‎ ‎（1）若椭圆C的离心率为，其“伴随”与直线x+y﹣2=0相切，求椭圆C的方程．‎ ‎（2）设椭圆E： +=1，P为椭圆C上任意一点，过点P的直线y=kx+m交椭圆E于AB两点，射线PO交椭圆E于点Q．‎ ‎（i）求的值；‎ ‎（ii）求△ABQ面积的最大值．‎ ‎【考点】直线与椭圆的位置关系．‎ ‎【分析】（Ⅰ）运用椭圆的离心率公式和椭圆的“伴随”定义及a，b，c的关系，计算即可得到a，b，进而得到椭圆C的方程；‎ ‎（Ⅱ）求得椭圆E的方程，（i）设P（x0，y0），=λ，求得Q的坐标，分别代入椭圆C，E的方程，化简整理，即可得到所求值；‎ ‎（ii）设A（x1，y1），B（x2，y2），将直线y=kx+m代入椭圆E的方程，运用韦达定理，三角形的面积公式，将直线y=kx+m代入椭圆C的方程，由判别式大于0，可得t的范围，结合二次函数的最值，又△ABQ的面积为3S，即可得到所求的最大值．‎ ‎【解答】解：（1）∵椭圆C： +=1（a＞b＞0）的离心率为，其“伴随”与直线x+y﹣2=0相切，‎ ‎∴，解得a=2，b=1，‎ ‎∴椭圆C的方程为=1．‎ ‎（2）由（1）知椭圆E的方程为+=1，‎ ‎（i）设P（x0，y0），|=λ，由题意可知，‎ Q（﹣λx0，﹣λy0），由于+y02=1，‎ 又+=1，即（+y02）=1，‎ 所以λ=2，即|=2；‎ ‎（ii）设A（x1，y1），B（x2，y2），将直线y=kx+m代入椭圆E的方程，可得 ‎（1+4k2）x2+8kmx+4m2﹣16=0，由△＞0，可得m2＜4+16k2，①‎ 则有x1+x2=﹣，x1x2=，‎ 所以|x1﹣x2|=，‎ 由直线y=kx+m与y轴交于（0，m），‎ 则△AOB的面积为S=|m|•|x1﹣x2|=|m|•=2，‎ 设=t，则S=2，‎ 将直线y=kx+m代入椭圆C的方程，可得（1+4k2）x2+8kmx+4m2﹣4=0，‎ 由△＞0可得m2＜1+4k2，②‎ 由①②可得0＜t＜1，则S=2在（0，1）递增，即有t=1取得最大值，‎ 即有S，即m2=1+4k2，取得最大值2，‎ 由（i）知，△ABQ的面积为3S，‎ 即△ABQ面积的最大值为6．‎ ‎【点评】本题考查椭圆的方程和性质，主要考查直线方程和椭圆方程联立，运用韦达定理，同时考查三角形的面积公式和二次函数的最值，属于中档题．‎ ‎　‎