2020_2021学年新教材高中数学第十章概率10

2020_2021学年新教材高中数学第十章概率10

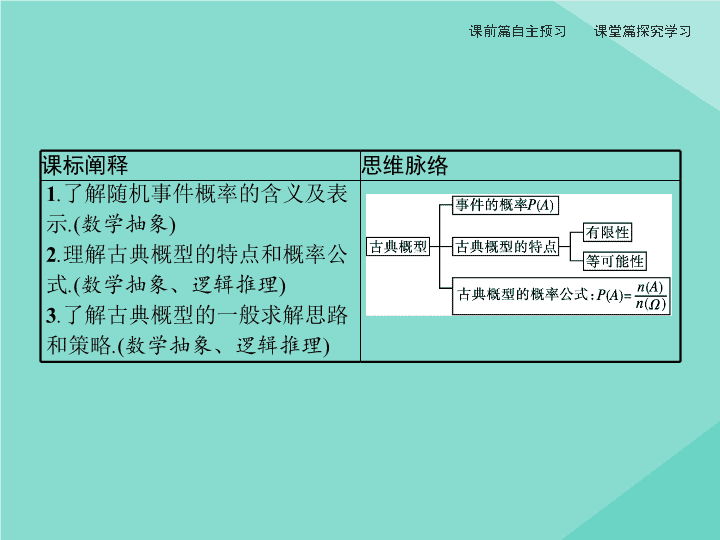
10 . 1 . 3 　 古典概型 课标阐释 思维脉络 1 . 了解随机事件概率的含义及表示 . ( 数学抽象 ) 2 . 理解古典概型的特点和概率公式 . ( 数学抽象、逻辑推理 ) 3 . 了解古典概型的一般求解思路和策略 . ( 数学抽象、逻辑推理 ) 激趣诱思 知识点拨 古典概型也叫传统概率 , 其定义是由法国数学家拉普拉斯 (Laplace) 提出的 . 如果一个随机试验所包含的样本点是有限的 , 且每个样本点发生的可能性均相等 , 则这个随机试验叫做拉普拉斯试验 , 这种条件下的概率模型就叫古典概型 . 古典概型是概率论中最直观和最简单的模型 , 概率的许多运算规则 , 也是在这种模型下得到的 . 激趣诱思 知识点拨 知识点一、随机事件的概率 对随机事件 发生可能性大小 的度量 ( 数值 ) 称为事件的概率 , 事件 A 的概率用 P ( A ) 表示 . 激趣诱思 知识点拨 知识 点二、古典概型 1 . 有限性 : 样本空间的样本点只有有限个 ; 2 . 等可能性 : 每个样本点发生的可能性相等 . 我们将具有以上两个特征的试验称为古典概型试验 , 其数学模型称为古典概率模型 , 简称古典概型 . 名师点析 (1) 由古典概型的定义可得古典概型满足基本事件的有限性和等可能性这两个重要特征 , 所以求事件的概率就可以不用通过大量的重复试验 , 而只要对一次试验中可能出现的结果进行分析和计算即可 . (2) 在古典概型中 , 每个基本事件发生的可能性都相等 , 称这些基本事件为等可能基本事件 . 激趣诱思 知识点拨 微思考 请根据试验一、试验二的要求完成下列问题 . (1) 试验一 : 抛掷一枚质地均匀的硬币 , 分别记录 “ 正面朝上 ” 和 “ 反面朝上 ” 的次数 , 要求每个数学小组至少完成 60 次 . (2) 试验二 : 抛掷一枚质地均匀的骰子 , 分别记录朝上一面出现 “1 点 ” 、 “2 点 ” 、 “3 点 ” 、 “4 点 ” 、 “5 点 ” 和 “6 点 ” 的次数 , 要求每个数学小组至少完成 60 次 . 问题 ① : 根据两个模拟试验的结果 , 完成下表 .   试验材料 试验中出现的各种结果 各结果之间有何关系 试验一 质地均匀的硬币     试验二 质地均匀的骰子     激趣诱思 知识点拨 问题 ② : 上述试验中出现的结果有什么特点 ? 提示 : 问题 ① :{ 正面向上 , 反面向上 } 　 互斥 　 {1,2,3,4,5,6} 　 互斥 问题 ② : 试验中所有可能出现的结果只有有限个 ; 每个结果出现的可能性相等 . 激趣诱思 知识点拨 微练习 下列试验中 , 是古典概型的个数为 ( 　　 ) ① 种下一粒花生 , 观察它是否发芽 ; ② 向上抛一枚质地不均的硬币 , 观察正面向上的概率 ; ③ 正方形 ABCD 内任意一点 P , 点 P 恰与点 C 重合 ; ④ 从 1,2,3,4 四个数中 , 任取两个数 , 求所取两数之一是 2 的概率 ; ⑤ 在线段 [0,5] 上任取一点 , 求此点小于 2 的概率 . A.0 　　　　　 B.1 　　　　　 C.2 　　　　　 D.3 解析 : 只有 ④ 是古典概型 . 答案 : B 激趣诱思 知识点拨 知识点三、古典概型的概率公式 一般地 , 设试验 E 是古典概型 , 样本空间 Ω 包含 n 个样本点 , 事件 A 包含其中的 k 个样本点 , 则定义事件 A 的 概率 其中 , n ( A ) 和 n ( Ω ) 分别表示事件 A 和样本空间 Ω 包含的样本点个数 . 名师点析 求解古典概型问题的一般思路 (1) 明确试验的条件及要观察的结果 , 用适当的符号 ( 字母、数字、数组等 ) 表示试验的可能结果 ( 借助图表可以帮助我们不重不漏地列出所有的可能结果 ); (2) 根据实际问题情境判断样本点的等可能性 ; (3) 计算样本点总个数及事件 A 包含的样本点个数 , 求出事件 A 的概率 . 激趣诱思 知识点拨 微思考 某汽车站每天均有 3 辆开往省城的分上、中、下等级的客车 . 某天王先生准备在该汽车站乘车去省城办事 , 但他不知道客车的车况 , 也不知道发车顺序 . 为了尽可能乘上上等车 , 他采取如下策略 : 先不上第一辆 , 如果第二辆比第一辆好则上第二辆 , 否则上第三辆 , 那么你能得出王先生能乘上上等车的概率吗 ? 提示 : 共有 6 种发车顺序 : ① 上、中、 下 ; ② 上、下、 中 ; ③ 中、 上 、下 ; ④ 中、下、 上 ; ⑤ 下、 中 、上 ; ⑥ 下、 上 、中 ( 其中画线的表示王先生所乘的车 ), 所以他乘上上等车的概率 为 探究一 探究二 探究三 素养形成 当堂检测 样本点的计数问题 例 1 (2020 山东潍坊高一检测 ) 将一枚质地均匀的骰子先后抛掷两次 , 观察两次出现的点数情况 , 则 : (1) 一共有几个样本点 ? (2)“ 出现的点数之和大于 8” 包含几个样本点 ? 分析 先列出所有的样本点 , 再确定个数 . 探究一 探究二 探究三 素养形成 当堂检测 解 : ( 方法一 ) (1) 用 ( x , y ) 表示样本点 , 其中 x 表示第 1 次骰子出现的点数 , y 表示第 2 次骰子出现的点数 , 则试验的样本空间 : Ω= {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2),(4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6)} . 共 36 个样本点 . (2) 设 A= “ 出现的点数之和大于 8”, 则 A= {(3,6),(4,5),(4,6),(5,4),(5,5),(5,6),(6,3),(6,4),(6,5),(6,6)}, 包含 10 个样本点 . 探究一 探究二 探究三 素养形成 当堂检测 ( 方法二 ) 如下图所示 , 坐标平面内的数表示相应两次抛掷后出现的点数的和 , 样本点与所描点一一对应 . (1) 由图知 , 样本点的总数为 36 . (2)“ 出现的点数之和大于 8” 包含 10 个样本点 ( 已用虚线圈出 ) . 探究一 探究二 探究三 素养形成 当堂检测 ( 方法三 ) 一枚骰子先后抛掷两次的所有可能结果用树形图表示 . 如下图所示 . (1) 由图知 , 共 36 个样本点 . (2)“ 出现的点数之和大于 8” 包含 10 个样本点 ( 已用 “ √ ” 标出 ) . 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 1 . 在列出样本点时 , 应先确定样本点是否与顺序有关 . 写样本点时 , 一定要按一定顺序写 , 这样不容易漏写 . 2 . 求样本点总数的常用方法 (1) 列举法 : 适合于较简单的问题 . (2) 列表法 : 适合求较复杂问题中的样本点数 . (3) 树形图法 : 适合较复杂问题中样本点的探求 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 1 袋中有 2 个标号分别为 1,2 的白球和 2 个标号分别为 3,4 的黑球 , 这 4 个球除颜色、标号外完全相同 ,4 个人按顺序依次从中摸出 1 个球 , 求样本点的个数 . 探究一 探究二 探究三 素养形成 当堂检测 解 : 4 个人按顺序依次从袋中摸出 1 个球的所有可能结果用树形图表示如图 : 共 24 个样本点 . 探究一 探究二 探究三 素养形成 当堂检测 古典概型的多种求解策略 例 2 一个盒子中放有 5 个完全相同的小球 , 其上分别标有号码 1,2,3,4,5 . 从中任取一个 , 记下号码后放回 . 再取出 1 个 , 记下号码后放回 , 按顺序记录为 ( x , y ) . (1) 求所得两球标号的和为 6 的概率 ; (2) 求所得两球标号的和是 3 的倍数的概率 . 探究一 探究二 探究三 素养形成 当堂检测 解 : 列出所有的样本点 , 共 25 个 , 如图所示 . (1) 设 A= “ 所得两球标号的和为 6”, 则由图可直观地看出 A= {(1,5),(2,4),(3,3),(4,2),(5,1)}, 故所求概率 为 (2) 设 B= “ 两球标号的和为 3 的倍数 ”, 则 B= {(2,1),(1,2),(1,5),(2,4),(3,3),(5,1),(4,2),(4,5),(5,4)}, 共 9 个样本点 , 故所求概率 为 . 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 1 . 求解古典概型 “ 四步法 ” 探究一 探究二 探究三 素养形成 当堂检测 2 . 列表法求解样本点个数的思路 列表法就是利用表格的形式列出所有的样本点 , 通常用来解决试验中包含两个或两个以上的元素 , 且试验结果比较多的问题 . 表格的行与列分别代表不同的元素 , 根据试验的要求直接在表格中标出相应的结果 , 这种方法直观、简洁、不易出错 . 3 . 用坐标系来表示样本点多用于二维或三维问题 , 并且往往表达含有顺序问题的样本点 , 但要求元素不宜过多 . 4 . 树形图可以清晰准确地列出所有的样本点 , 画树形图求概率的基本步骤 : (1) 明确一次试验的几个步骤及顺序 ; (2) 画树形图列举一次试验的所有可能结果 ; (3) 明确样本点 , 数出 n ( A ), n ( Ω ); (4) 计算随机事件的概率 P ( A ) = . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 2 甲、乙、丙三个盒中分别装有大小、形状相同的卡片若干 , 甲盒中装有 2 张卡片 , 分别写有字母 A 和 B; 乙盒中装有 3 张卡片 , 分别写有字母 C 、 D 和 E; 丙盒中装有 2 张卡片 , 分别写有字母 H 和 I. 现要从 3 个盒中各随机取出一张卡片 . 求 : (1) 取出的 3 张卡片中恰好有 1 张 ,2 张 ,3 张写有元音字母的概率分别是多少 ? (2) 取出的 3 张卡片上全是辅音字母的概率是多少 ? 探究一 探究二 探究三 素养形成 当堂检测 解 : 根据题意 , 可画出如下树形图 : 探究一 探究二 探究三 素养形成 当堂检测 古典概型与其他统计知识的交汇问题 例 3 (2019 湖南高一期末 ) 某校从高一年级某次数学竞赛的成绩中随机抽取 100 名学生的成绩 , 分组为 [50,60),[60,70),[70,80),[80,90),[90,100], 统计后得到频率分布直方图如图所示 . (1) 试估计这组样本数据的众数和 中位数 ( 结果精确到 0 . 1) . (2) 年级决定在成绩 [70,100] 中用分层随机抽样抽取 6 人组成一个调研小组 , 对高一年级学生课外学习数学的情况做一个调查 , 则在 [70,80),[80,90),[90,100] 这三组分别抽取了多少人 ? (3) 现在要从 (2) 中抽取的 6 人中选出正、副 2 个小组长 , 求成绩在 [80,90) 中至少有 1 人当选为正、副小组长的概率 . 探究一 探究二 探究三 素养形成 当堂检测 分析 (1) 由频率分布直方图能求出众数、中位数 . (2) 先求出成绩为 [70,80),[80,90),[90,100) 这三组的频率 , 由此能求出 [70,80),[80,90),[90,100] 这三组抽取的人数 . (3) 由 (2) 知成绩在 [70,80) 有 3 人 , 分别记为 a , b , c ; 成绩在 [80,90) 有 2 人 , 分别记为 d , e ; 成绩在 [90,100] 有 1 人 , 记为 f. 由此利用列举法能求出成绩在 [80,90) 中至少有 1 人当选为正、副小组长的概率 . 探究一 探究二 探究三 素养形成 当堂检测 成绩 在 [50,70) 内的频率为 (0 . 005 + 0 . 035) × 10 = 0 . 4, 成绩在 [70,80) 内的频率为 0 . 03 × 10 = 0 . 3, ( 2) 成绩为 [70,80),[80,90),[90,100] 这三组的频率分别为 0 . 3,0 . 2,0 . 1, ∴ [70,80),[80,90),[90,100] 这三组抽取的人数分别为 3,2,1 . 探究一 探究二 探究三 素养形成 当堂检测 (3) 由 (2) 知成绩在 [70,80) 有 3 人 , 分别记为 a , b , c ; 成绩在 [80,90) 有 2 人 , 分别记为 d , e ; 成绩在 [90,100] 有 1 人 , 记为 f. 用 x 1 , x 2 表示从 [70,80),[80,90),[90,100] 这三组中抽取的 2 人 , 则数组 ( x 1 , x 2 ) 表示这个试验的一个样本点 . ∴ 设 A= “ 从抽取的 6 人中选出正、副 2 个小组长 ”, 则 A= {( a , b ),( b , a ),( a , c ),( c , a ),( a , d ),( d , a ),( a , e ),( e , a ),( a , f ),( f , a ),( b , c ),( c , b ),( b , d ),( d , b ),( b , e ),( e , b ),( b , f ),( f , b ),( c , d ),( d , c ),( c , e ),( e , c ),( c , f ),( f , c ),( d , e ),( e , d ),( d , f ),( f , d ),( e , f ),( f , e )} . 记 “ 成绩在 [80,90) 中至少有 1 人当选为正、副小组长 ” 为事件 Q , 则事件 Q 包含的样本点有 18 个 , ∴ 成绩在 [80,90) 中至少有 1 人当选为正、副小组长的 概率 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 概率问题常常与统计问题综合考查 , 在此类问题中 , 概率与频率的区别并不是十分明显 , 通常直接用题目中的频率代替概率进行计算 . 探究一 探究二 探究三 素养形成 当堂检测 延伸探究 从某校高二年级 800 名男生中随机抽取 50 名测量其身高 ( 单位 :cm, 被测学生的身高全部在 155 cm 到 195 cm 之间 ), 将测量结果按如下方式分成 8 组 : 第一组 [155,160), 第二组 [160,165),…, 第八组 [190,195], 绘制成的频率分布直方图如图所示 , 若从 身高 位于第六组和第八组的男生中随机抽取 2 名 , 记他们的身高分别为 x , y , 则 |x-y| ≤5 的概率为 ( 　　 ) 探究一 探究二 探究三 素养形成 当堂检测 解析 : 由频率分布直方图 , 可知身高在 [180,185) 的人数为 0 . 016 × 5 × 50 = 4, 分别记为 a , b , c , d ; 身高在 [190,195) 的人数为 0 . 008 × 5 × 50 = 2, 分别记为 A , B , 设第一次抽取的人记为 x 1 , 第二次抽取的人记为 x 2 , 则可用数组 ( x 1 , x 2 ) 表示样本点 , M= “ 从身高位于第六组和第八组的男生中随机抽取 2 名 ”, 若 x , y ∈ [180,185], 则 M= {( a , b ),( a , c ),( a , d ),( b , c ),( b , d ),( c , d )}, 共 6 种情况 ; 若 x , y ∈ [190,195], 则 M= { AB }, 共 1 种情况 ; 若 x ∈ [180,185), y ∈ [190,195] 或 x ∈ [190,195], y ∈ [180,185), 则 M= {( a , A ),( b , A ),( c , A ),( d , A ),( a , B ),( b , B ),( c , B ),( d , B )}, 共 8 种情况 . 所以样本点的总数为 6 + 1 + 8 = 15, 而事件 “ |x-y| ≤5” 所包含的样本点数为 6 + 1 = 7, 故 P ( |x-y| ≤5 ) = . 答案 : A 探究一 探究二 探究三 素养形成 当堂检测 分类讨论思想的应用 典例 (2020 江苏徐州一中高二开学考试 ) 《易经》是中国传统文化中的精髓 , 下图是易经八卦图 ( 含乾、坤、巽、震、坎、离、艮、兑八卦 ), 每卦有三根线组成 (“ ” 表示一根阳线 ,“ ” 表示一根阴线 ), 从八卦中任取两卦 , 这两卦的六根线中恰有三根阳线和三根阴线的概率为 　　　　 .  探究一 探究二 探究三 素养形成 当堂检测 解析 : 记八卦分别为 1,2,3,4,5,6,7,8, 则从八卦中任取两卦 , 可能情况有 (1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(1,8),(2,3),(2,4),(2,5),(2,6),(2,7 ), ( 2,8),(3,4),(3,5),(3,6),(3,7),(3,8),(4,5),(4,6),(4,7),(4,8),(5,6),(5,7),(5,8),(6,7),(6,8),(7,8), 共 28 种取法 . 若两卦的六根线中恰有三根阳线和三根阴线 , 可按取得卦的阳、阴线的根数分类计算 : 当有一卦阳、阴线的根数为 3,0 时 , 另一卦阳、阴线的根数为 0,3, 共有 1 种取法 . 当有一卦阳、阴线的根数为 2,1 时 , 另一卦阳、阴线的根数为 1,2, 共有 3 × 3 = 9( 种 ) 取法 . 探究一 探究二 探究三 素养形成 当堂检测 所以两卦的六根线中恰有三根阳线和三根阴线的取法有 1 + 9 = 10( 种 ) . 则从八卦中任取两卦 , 这两卦的六根线中恰有三根阳线和三根阴线的概率 为 探究一 探究二 探究三 素养形成 当堂检测 1 . 标有数字 1,2,3,4,5 的卡片各一张 , 从这 5 张卡片中随机抽取 1 张 , 不放回地再随机抽取 1 张 , 则抽取的第一张卡片上的数大于第二张卡片上的数的概率为 ( 　　 ) 解析 : 如图 : 样本点的总数为 20, 其中第一张卡片上的数大于第二张卡片上的数包括的样本点个数是 10 个 , 故所求 概率 答案 : A 探究一 探究二 探究三 素养形成 当堂检测 2 . (2020 江西高一月考 ) 《史记》中讲述了田忌与齐王赛马的故事 . “ 田忌的上等马优于齐王的中等马 , 劣于齐王的上等马 ; 田忌的中等马优于齐王的下等马 , 劣于齐王的中等马 ; 田忌的下等马劣于齐王的下等马 . ” 双方从各自的马匹中随机选一匹进行一场比赛 , 则田忌的马获胜的概率为 ( 　　 ) 探究一 探究二 探究三 素养形成 当堂检测 解析 : 设齐王的上 , 中 , 下三个等次的马分别为 a , b , c , 田忌的上 , 中 , 下三个等次的马分别记为 A , B , C , x 1 表示从齐王的马匹中抽取的一匹马 , x 2 表示从田忌的马匹中抽取的一匹马 , 则数组 ( x 1 , x 2 ) 表示这个试验的一个样本点 , 设 A= “ 从双方的马匹中随机选一匹进行一场比赛 ”, B= “ 田忌获胜 ”, 则 A= {( A , a ),( A , b ),( A , c ),( B , a ),( B , b ),( B , c ),( C , a ),( C , b ),( C , c )}, 根据题意 , 其中 B= {( A , b ),( A , c ),( B , c )}, 则田忌获胜的概率 为 . 故选 A . 答案 : A 探究一 探究二 探究三 素养形成 当堂检测 3 . 将一颗骰子掷两次 , 观察出现的点数 , 并记第一次出现的点数为 m , 第二次出现的点数为 n , 向量 p = ( m , n ), q = (2,6), 则向量 p 与 q 共线的概率为 　　　　 .  解析 : ∵ 试验的样本空间 Ω= {( m , n ) |m , n ∈ 1,2,3,4,5,6}, ∴ n ( Ω ) = 36, 满足条件的事件是使向量 p = ( m , n ) 与 q = (2,6) 共线 , 即 6 m- 2 n= 0, ∴ n= 3 m , 满足这种条件的有 (1,3),(2,6), 共有 2 种结果 , ∴ 向量 p 与 q 共线的 概率 探究一 探究二 探究三 素养形成 当堂检测 4 . 现有 5 根竹竿 , 它们的长度 ( 单位 :m) 分别为 2 . 5,2 . 6,2 . 7,2 . 8,2 . 9, 若从中一次随机抽取 2 根竹竿 , 则它们的长度恰好相差 0 . 3 m 的概率为 　　　　　 .  解析 : 从 5 根竹竿中一次随机抽取 2 根有 10 种等可能结果 , 它们的长度恰好相差 0 . 3 m 的可能结果有两种 , 分别是 :2 . 5 和 2 . 8,2 . 6 和 2 . 9, 所求概率 为 探究一 探究二 探究三 素养形成 当堂检测 5 . 某企业为了解下属某部门对本企业职工的服务情况 , 随机访问 50 名职工 . 根据这 50 名职工对该部门的评分 , 绘制频率分布直方图 ( 如图所示 ), 其中样本数据分组区间为 [40,50),[50,60),…,[80,90),[90,100] . (1) 求频率分布直方图中 a 的值 ; (2) 估计该企业的职工对该部门评分不低于 80 的频率 ; (3) 从评分在 [40,60) 的受访职工中 , 随机抽取 2 人 , 求此 2 人的评分都在 [40,50) 的概率 . 探究一 探究二 探究三 素养形成 当堂检测 解 : (1) 因为 (0 . 004 +a+ 0 . 018 + 0 . 022 × 2 + 0 . 028) × 10 = 1, 所以 a= 0 . 006 . (2) 由所给频率分布直方图知 ,50 名受访职工评分不低于 80 的频率为 (0 . 022 + 0 . 018) × 10 = 0 . 4, 所以估计该企业职工对该部门评分不低于 80 的频率为 0 . 4 . (3) 受访职工中评分在 [50,60) 的有 50 × 0 . 006 × 10 = 3( 人 ), 记为 A 1 , A 2 , A 3 ; 受访职工中评分在 [40,50) 的有 50 × 0 . 004 × 10 = 2( 人 ), 记为 B 1 , B 2 . 设 x 1 , x 2 为从评分在 [40,60) 的受访职工中随机抽取的 2 人 , 则 ( x 1 , x 2 ) 表示一个样本点 , A= “ 从评分在 [40,60) 的受访职工中 , 随机抽取 2 人 ”, 则 A= {( A 1 , A 2 ),( A 1 , A 3 ),( A 1 , B 1 ),( A 1 , B 2 ),( A 2 , A 3 ),( A 2 , B 1 ),( A 2 , B 2 ),( A 3 , B 1 ),( A 3 , B 2 ),( B 1 , B 2 )}, 共 10 种结果 , 又因为所抽取 2 人的评分都在 [40,50) 的结果有 1 种 , 故所求的概率 P = .