- 2021-06-16 发布 |
- 37.5 KB |
- 14页

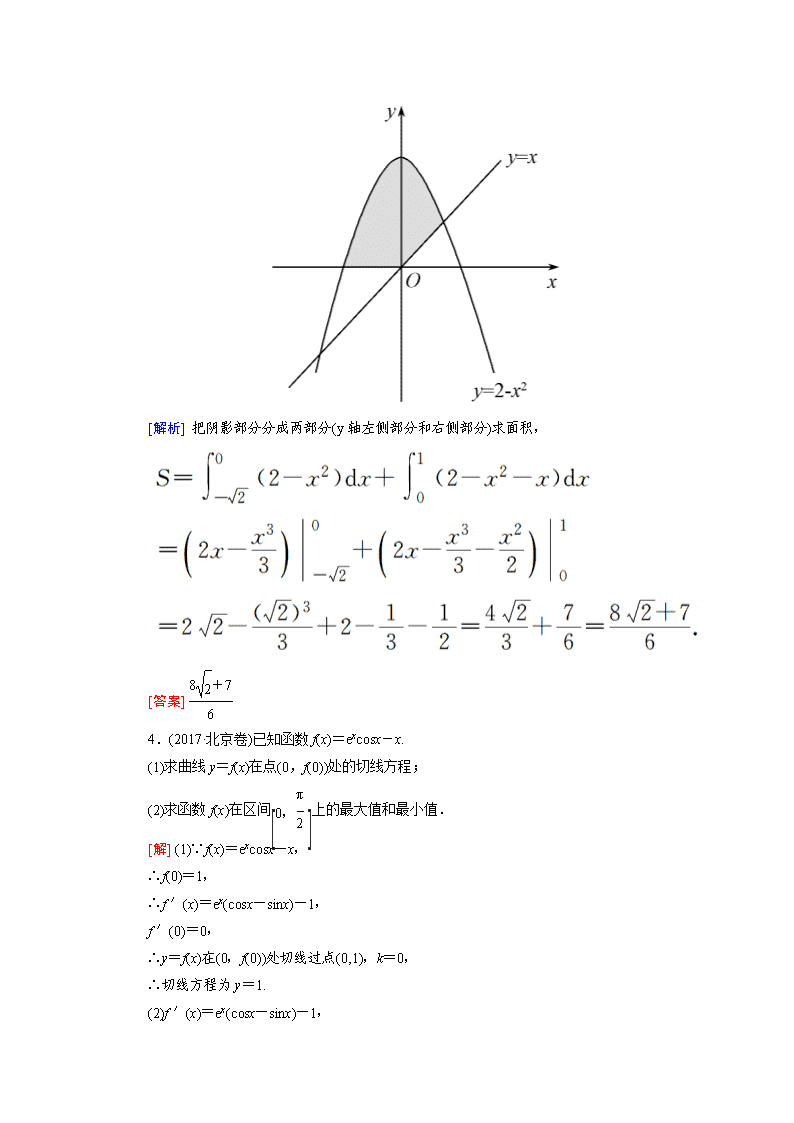

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习北师大版导数的简单应用学案
专题一 集合、常用逻辑用语、不等式、函数与导数 第五讲 导数的简单应用 高考导航 导数的意义和运算是导数应用的基础,是高考的一个热点. 2.利用函数的单调性和最值确定函数的解析式或参数的值,突出考查导数的工具性作用. 1.(2017·福州质检)函数f(x)=x3-ax为R上增函数的一个充分不必要条件是( ) A.a≤0 B.a<0 C.a≥0 D.a>0 [解析] 函数f(x)=x3-ax为R上增函数的一个充分不必要条件是f ′(x)=3x2-a>0在R上恒成立,所以a<(3x2)min.因为(3x2)min=0,所以a<0.故选B. [答案] B 2.(2017·全国卷Ⅱ)若x=-2是函数f(x)=(x2+ax-1)ex-1的极值点,则f(x)的极小值为( ) A.-1 B.-2e-3 C.5e-3 D.1 [解析] 由题意可得f′(x)=ex-1[x2+(a+2)x+a-1]. ∵x=-2是函数f(x)=(x2+ax-1)ex-1的极值点, ∴f ′(-2)=0,∴a=-1,∴f(x)=(x2-x-1)ex-1,f ′(x)=ex-1(x2+x-2)=ex-1(x-1)(x+2), ∴x∈(-∞,-2),(1,+∞)时,f ′(x)>0,f(x)单调递增;x∈(-2,1)时,f ′(x)<0,f(x)单调递减. ∴f(x)极小值=f(1)=-1.故选A. [答案] A 3.(2017·衡水中学三模)由曲线y=2-x2,直线y=x及x轴所围成的封闭图形(图中的阴影部分)的面积是________. [解析] 把阴影部分分成两部分(y轴左侧部分和右侧部分)求面积, [答案] 4.(2017·北京卷)已知函数f(x)=excosx-x. (1)求曲线y=f(x)在点(0,f(0))处的切线方程; (2)求函数f(x)在区间上的最大值和最小值. [解] (1)∵f(x)=excosx-x, ∴f(0)=1, ∴f ′(x)=ex(cosx-sinx)-1, f ′(0)=0, ∴y=f(x)在(0,f(0))处切线过点(0,1),k=0, ∴切线方程为y=1. (2)f ′(x)=ex(cosx-sinx)-1, 设f ′(x)=g(x), ∴g′(x)=-2sinx·ex≤0, ∴g(x)在上单调递减, ∴g(x)≤g(0)=0,∴f′(x)≤0, ∴f(x)在上单调递减, ∴f(x)max=f(0)=1, f(x)min=f=-. 考点一 导数的几何意义与定积分 1.导数公式 (1)(sinx)′=cosx; (2)(cosx)′=-sinx; (3)(ax)′=axlna(a>0); (4)(logax)′=(a>0,且a≠1). 2.导数的几何意义 函数f(x)在x0处的导数是曲线f(x)在点P(x0,f(x0))处的切线的斜率,曲线f(x)在点P处的切线的斜率k=f ′(x0),相应的切线方程为y-f(x0)=f ′(x0)·(x-x0). 3.微积分基本定理 一般地,如果f(x)是区间[a,b]上的连续函数,并且F′(x)=f(x),那么f(x)dx=F(b)-F(a). [对点训练] 1.(2017·大同模拟)过点(1,-1)且与曲线y=x3-2x相切的切线方程为( ) A.x-y-2=0或5x+4y-1=0 B.x-y-2=0 C.x-y+2=0 D.x-y-2=0或4x+5y+1=0 [解析] 设切点坐标为(x0,y0),y0=x-2x0,则曲线在(x0,y0)处的切线斜率为y′=3x-2,当x0=1时斜率为1,切线方程为x-y-2=0,当x0≠1时,过(1,-1)点的切线的斜率为=x+x0-1=3x-2,解得x0=-,其斜率为-,切线方程为5x+4y-1=0,所以A正确. [答案] A 2.(2017·北京卷改编)已知函数f(x)=excosx-x.则曲线y=f(x)在点(0,f(0))处的切线方程为_________________________. [解析] 因为f(x)=excosx-x,所以f ′(x)=ex(cosx-sinx)-1,f ′(0)=0. 又f(0)=1,所以曲线y=f(x)在点(0, f(0))处的切线方程为y=1. [答案] y=1 3.(2017·安徽示范高中二模)计算:(-x)dx=________. [解析] 由定积分的几何意义知dx是由y=与直线x=0,x=1所围成的图形的面积,即是以(1,0)为圆心,以1为半径的圆的面积的,故dx=,(-x)dx=-x2=-, ∴-x)dx=. [答案] 4.(2017·宁夏二模)曲线y=x2和直线x=0,x=1,y=所围成的图形(如图中阴影部分所示)的面积为________. [解析] 令x2=,得x=或x=-(舍去),所以所 [答案] (1)求曲线y=f(x)的切线方程的3种类型及方法 ①已知切点P(x0,y0),求y=f(x)过点P的切线方程: 求出切线的斜率f′(x0),由点斜式写出方程. ②已知切线的斜率为k,求y=f(x)的切线方程:设切点P(x0,y0),通过方程k=f′(x0)解得x0,再由点斜式写出方程. ③已知切线上一点(非切点),求y=f(x)的切线方程: 设切点P(x0,y0),利用导数求得切线斜率f′(x0),然后由斜率公式求得切线斜率,列方程(组)解得x0,再由点斜式或两点式写出方程. (2)求定积分的2种方法 ①利用微积分基本定理求定积分; ②利用定积分的几何意义求定积分. 【易错提醒】 求曲线的切线方程时,务必分清点P处的切线还是过点P的切线,前者点P为切点,后者点P不一定为切点,求解时应先求出切点坐标. 考点二 利用导数研究函数的单调性 1.若求函数的单调区间(或证明单调性),只要在其定义域内解(或证明)不等式f ′(x)>0或f ′(x)<0即可. 2.若已知函数的单调性,则转化为不等式f ′(x)≥0或f ′(x)≤0在单调区间上恒成立问题来求解.角度1:根据函数的单调性,利用导数求某些参数的取值范围 A.(-∞,2] B.(-∞,4] C.(-∞,8] D.[-2,4] [解析] f′(x)=[x2+(2-c)x-c+5]ex,∵函数f(x)在区间上单调递增,等价于x2 +(2-c)x-c+5≥0对任意x∈恒成立,即(x+1)c≤x2+2x+5, ∴c≤对任意x∈恒成立, ∵x∈,∴=(x+1)+≥4,当且仅当x=1时等号成立,∴c≤4. [答案] B [探究追问] 例1-1中若f(x)=(x2-cx+5)ex在上存在减区间,则实数c的取值范围是________. [解析] f′(x)=[x2+(2-c)x-c+5]ex,∵函数f(x)在上存在减区间,所以f ′(x)<0在上有解,即x2+(2-c)x-c+5<0在上有解,得c>在上有解. ∵x∈,∴=(x+1)+的最小值为4,∴c>4. [答案] (4,+∞) 角度2:利用函数的单调性与导数的关系,讨论含有参数的较复杂基本函数的单调性 [思维流程] →→ [解] f(x)的定义域为(0,+∞), f′(x)=a--+=. 当a≤0时,x∈(0,1)时,f′(x)>0,f(x)单调递增, x∈(1,+∞)时,f′(x)<0,f(x)单调递减. 当a>0时, f′(x)=. (1)0查看更多
相关文章
- 当前文档收益归属上传用户