- 2021-06-16 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习北师大版统计与统计案例(文)学案
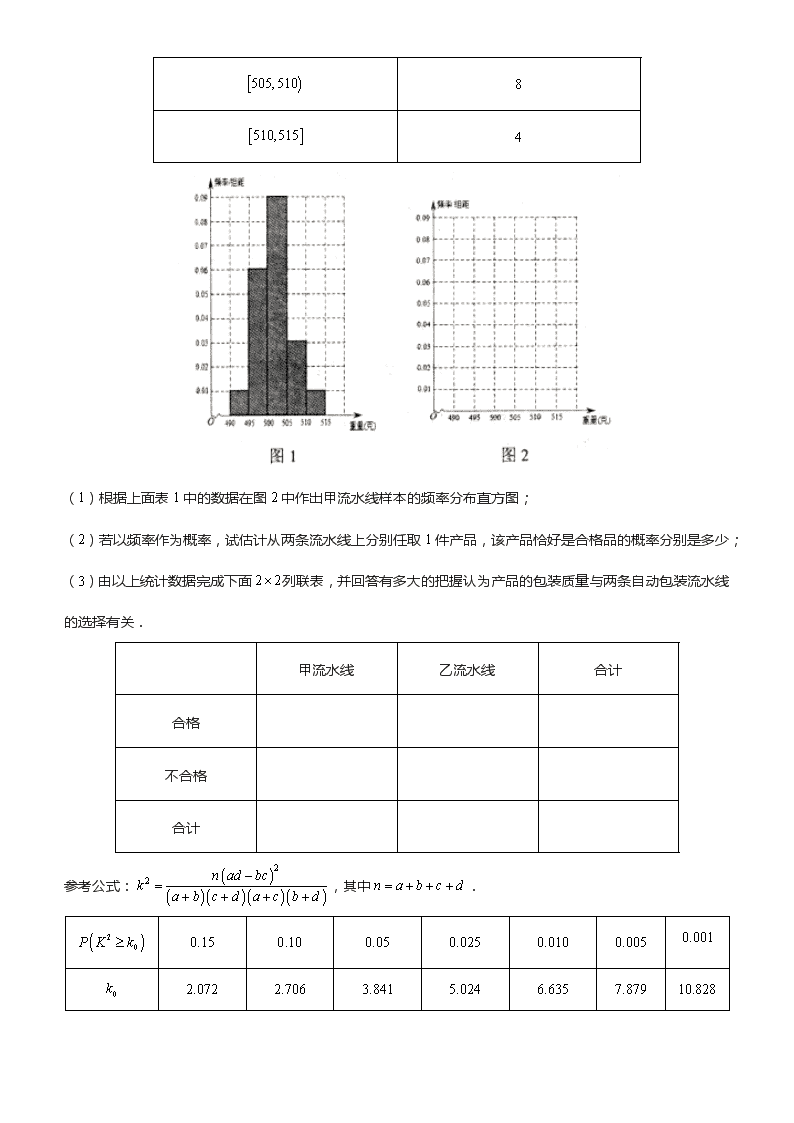
[2019·开封一模] 大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程. (1)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过的前提下认为学习先修课程与优等生有关系? 优等生 非优等生 总计 学习大学先修课程 250 没有学习大学先修课程 总计 150 (2)某班有5名优等生,其中有2名参加了大学生先修课程的学习,在这5名优等生中任选3人进行测试,求这3人中至少有1名参加了大学先修课程学习的概率. 参考数据: 参考公式:,其中. 【答案】(1)列联表见解析,有关系;(2). 【解析】(1)列联表如下: 优等生 非优等生 总计 学习大学先修课程 50 200 250 没有学习大学先修课程 100 900 1000 总计 150 1100 1250 由列联表可得, 因此在犯错误的概率不超过的前提下认为学习先修课程与优等生有关系. (2)在这5名优等生中,记参加了大学先修课程的学习的2名学生为,, 记没有参加大学先修课程学习的3名学生为,,. 则所有的抽样情况如下:,,,,, ,,,,,共10种, 其中没有学生参加大学先修课程学习的情况有1种,为. 记事件为至少有1名学生参加了大学先修课程的学习,则. 1.[2019·驻马店期末]某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在内的产品为合格品,否则为不合格品.注:表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图. 产品重量(克) 频数 6 8 14 8 4 (1)根据上面表1中的数据在图2中作出甲流水线样本的频率分布直方图; (2)若以频率作为概率,试估计从两条流水线上分别任取1件产品,该产品恰好是合格品的概率分别是多少; (3)由以上统计数据完成下面列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关. 甲流水线 乙流水线 合计 合格 不合格 合计 参考公式:,其中. 2.[2019·肇庆统测]下图是某市年至年环境基础设施投资额 (单位:亿元)的条形图. (1)若从年到年的五年中,任意选取两年,则这两年的投资额的平均数不少于亿元的概率; (2)为了预测该市年的环境基础设施投资额,建立了与时间变量的两个线性回归模型.根据年至年的数据(时间变量的值依次为1,2,,17)建立模型①:;根据年至年的数据(时间变量的值依次为1,2,,7)建立模型②:. (i)分别利用这两个模型,求该地区年的环境基础设施投资额的预测值; (ii)你认为用哪个模型得到的预测值更可靠?并说明理由. 3.[2019·衡水中学]为提高玉米产量,某种植基地对单位面积播种数与每棵作物的产量之间的关系进行了研究,收集了块试验田的数据,得到下表: 试验田编号 1 2 3 4 5 6 7 8 9 11 (棵/) 4 8 10 (斤/棵) 技术人员选择模型作为与的回归方程类型,令,相关统计量的值如下表: 600 44 2721 45642 由表中数据得到回归方程后进行残差分析,残差图如图所示: (1)根据残差图发现一个可疑数据,请写出可疑数据的编号(给出判断即可,不必说明理由); (2)剔除可疑数据后,由最小二乘法得到关于的线性回归方程中的,求关于的回归方程; (3)利用(2)得出的结果,计算当单位面积播种数为何值时,单位面积的总产量的预报值最大?(计算结果精确到) 附:对于一组数据,,,其回归直线的斜率和截距的最小二乘法估计分别为,,. 1.【答案】(1)见解析; (2)从甲流水线上任取1件产品,该产品恰好是合格品的概率为, 从乙流水线上任取1件产品,该产品恰好是合格品的概率为; (3)见解析. 【解析】(1)甲流水线样本的频率分布直方图如下: (2)由表1知甲流水线样本中合格品数为, 故甲流水线样本中合格品的频率为, 由图1知乙流水线样本中合格品的频率为, 据此可估计从甲流水线上任取1件产品,该产品恰好是合格品的概率为; 从乙流水线上任取1件产品,该产品恰好是合格品的概率为. (3)由(2)知甲流水线样本中合格品数为30,乙流水线样本中合格品数为. 列联表如下: 甲流水线 乙流水线 合计 合格 30 36 66 不合格 10 4 14 合计 40 40 80 ∵, ∴有的把握认为产品的包装质量与两条自动包装流水线的选择有关. 2.【答案】(1); (2)(i)利用模型①,预测值为亿元,利用模型②,预测值为亿元;(ii)见解析. 【解析】(1)从条形图中可知,2011年到2015年这五年的投资额分别为122亿、129亿、148亿、171亿、184亿,设2011年到2015年这五年的年份分别用,,,,表示, 则从中任意选取两年的所有基本事件有: ,,,,,,,,,,共10种, 其中满足两年的投资额的平均数不少于140亿元的所有基本事件有: ,,,,,,,共7种, ∴从2011年到2015年的五年中,任意选取两年,则这两年的投资额的平均数不少于140亿元的概率为. (2)(i)利用模型①,该地区2019年的环境基础设施投资额的预测值为 (亿元). 利用模型②,该地区2019年的环境基础设施投资额的预测值为 (亿元). (ii)利用模型②得到的预测值更可靠. 理由如下:画出2001年至2017年环境基础设施投资额 (单位:亿元)的散点图 (i)从散点图可以看出,2001年至2017年的数据对应的点没有随机散布在直线上下. 这说明利用2001年至2017年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势. 2011年相对2010年的环境基础设施投资额有明显增加, 2011年至2017年的数据对应的点位于一条直线的附近, 这说明从2011年开始环境基础设施投资额的变化规律呈线性增长趋势, 利用2011年至2017年的数据建立的线性模型可以较好地描述2011年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠. (ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元, 由模型①得到的预测值亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理. 说明利用模型②得到的预测值更可靠. 3.【答案】(1);(2);(3). 【解析】(1)可疑数据为第组. (2)剔除数据后,在剩余的组数据中, , ∴, ∴关于的线性回归方程为,则关于的回归方程为. (3)根据(2)的结果并结合条件,单位面积的总产量的预报值, , 当且仅当时,等号成立,此时, 即当时,单位面积的总产量的预报值最大,最大值是.查看更多