- 2021-06-16 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】宁夏银川市贺兰县景博中学2019-2020学年高一上学期第一次月考数学试题(解析版)
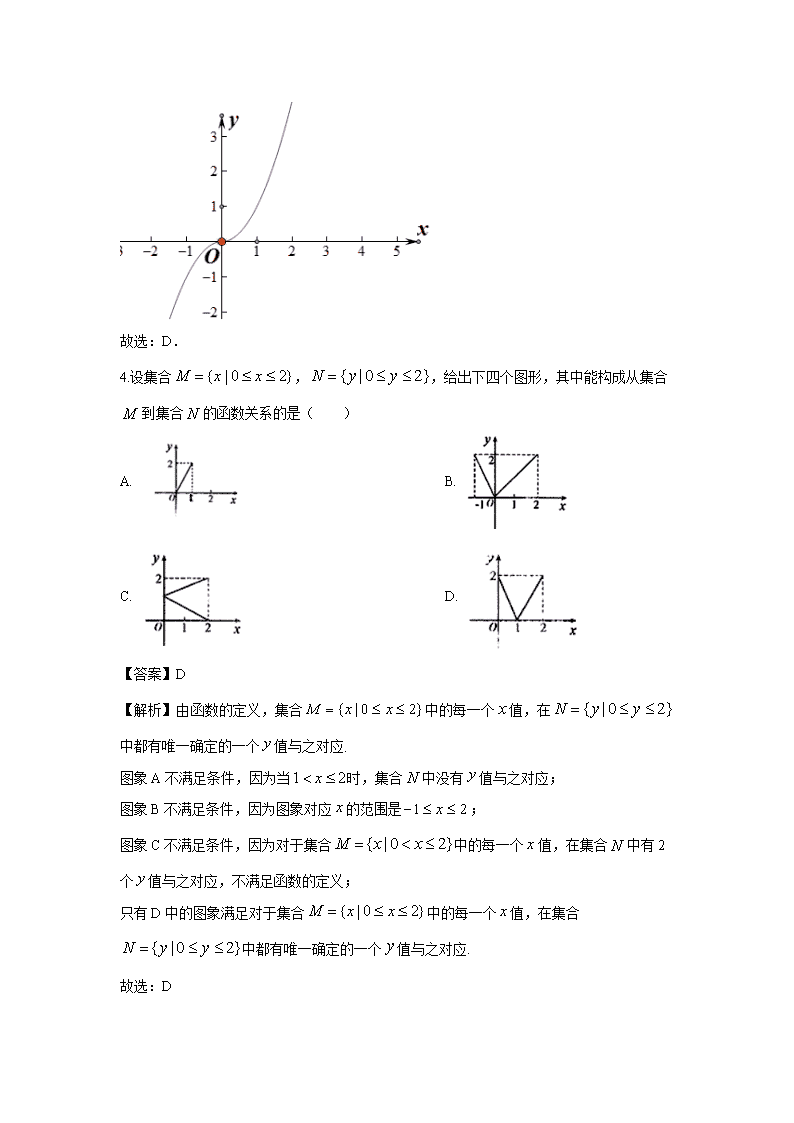
宁夏银川市贺兰县景博中学2019-2020学年高一上学期 第一次月考数学试题 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上; 一、选择题(本题共计12小题,每题5分,共计60分) 1.集合用列举法表示是( ) A. {1,2,3,4} B. {1,2,3,4,5} C. {0,1,2,3,4,5} D. {0,1,2,3,4} 【答案】D 【解析】由题意,又,∴集合为. 2.已知集合,若,则实数的值为( ) A. B. C. 或 D. 或 【答案】C 【解析】因为集合,且,所以或,当时,,适合题意;当时,,,也适合题意,所以实数的值为或. 故选:C. 3.下列函数中,既是奇函数又是在其定义域上是增函数的是( ) A. B. C. D. 【答案】D 【解析】选项A中,函数为非奇非偶函数,不符合题意; 选项B中,函数为奇函数,但在定义域为减函数,不符合题意; 选项C中,函数为奇函数,但在定义域不是增函数,不符合题意; 选项D中,如图所示:函数为奇函数,且在R上为增函数,符合题意; 故选:D. 4.设集合,,给出下四个图形,其中能构成从集合到集合的函数关系的是( ) A. B. C. D. 【答案】D 【解析】由函数的定义,集合中的每一个值,在中都有唯一确定的一个值与之对应. 图象A不满足条件,因为当时,集合中没有值与之对应; 图象B不满足条件,因为图象对应的范围是; 图象C不满足条件,因为对于集合中的每一个值,在集合中有2个值与之对应,不满足函数的定义; 只有D中的图象满足对于集合中的每一个值,在集合中都有唯一确定的一个值与之对应. 故选:D 5.函数的定义域是( ) A. (–1,+∞) B. (–1,1)∪(1,+∞) C. [–1,+∞) D. [–1,1)∪(1,+∞) 【答案】D 【解析】要使函数有意义,必须满足, 解得,且, 所以函数定义域是, 故选D. 6.设,,,则的大小顺序为( ) A. B. C. D. 【答案】B 【解析】由题意,根据实数指数幂的运算性质,可得,,, 又由函数是R上的单调递增函数, 因为,所以,即. 故选:B 7.函数f(x)=2x2-mx+3,当x∈[-2,+∞)时,f(x)是增函数,当x∈(-∞,-2]时,f(x)是减函数,则f(1)的值为( ) A. -3 B. 13 C. 7 D. 5 【答案】B 【解析】由题意知函数的对称轴,所以, 所以,故选B. 8.函数y=ax﹣1+2(a>0且a≠1)图象一定过点( ) A. (1,1) B. (1,3) C. (2,0) D. (4,0) 【答案】B 【解析】由x﹣1=0,解得x=1,此时y=1+2=3, 即函数的图象过定点(1,3),故选B 9.已知集合,则( ) A. B. C. D. 【答案】B 【解析】因为, 所以,故选B. 10.设,则的值为( ) A. 16 B. 18 C. 21 D. 24 【答案】B 【解析】.故选:B 11.已知是R上的增函数,则实数的取值范围是( ) A. B. C. D. 【答案】D 【解析】已知是上的增函数,则 ,则,选D. 12.已知是定义域为的奇函数,满足.若,则( ) A. B. C. D. 【答案】C 【解析】因为是定义域为的奇函数,且, 所以, 因此, 因为,所以, ,从而,选C. 二、填空题(本题共计4小题,每题5分,共计20分) 13.下列集合表示同一集合的是____________ . ①,②, ③④. 【答案】② 【解析】对于①,在平面直角坐标系中,点和点不是同一个点,则; 对于②,集合、中的元素都相同,则; 对于③,集合是点集,集合为数集,则; 对于④,集合是数集,集合是点集,则. 故答案为:② 14.函数的增区间是________________ . 【答案】 【解析】函数的定义域为,令,则, 因为在R上单调递减, 而上单调递减, 所以函数的增区间为.故答案为: 15.已知且函数的图象过点,则的值为 _______________ . 【答案】 【解析】,, 又函数的图象过点,所以,解得:. 故答案为: 16.若函数在上的最大值比最小值大,则的值为____________. 【答案】或 【解析】若,∴函数在区间上单调递减,所以,由题意得,又,故.若,∴函数在区间上单调递增,所以,由题意得,又,故. 答案:或 三、解答题(本题共计6小题,共计70分) 17.求下列各式的值: (1). (2)设,求 的值. 解:(1)原式; (2), . 18.设全集为R,,,. (1)求,; (2)若,求实数的取值范围. 解:(1), 或; (2),若,满足题意; 若,则,解得或, 综上,的取值范围是或. 19.已知函数是定义在上的奇函数,且. (1)求函数的解析式; (2)用定义证明:函数在上增函数. 解:(1)由题意得:,所以,所以, 又,即,解之得:, ; (2)设,则有, ,,,,, ,在上是增函数. 20.已知函数是R上的奇函数,且当时,. ①求函数的解析式; ②画出函数的图象,根据图象写出函数的单调区间. 解: ①∵函数是定义在R上的奇函数,∴. 当时,,. ∴函数的解析式为 ②函数图象如图所示: 由图象可知,函数的单调递减区间为,无单调递增区间. 21.已知函数 (1)若在上是增函数,求的取值范围; (2)若,求函数在区间上的最大值. 解:(1)因为,且在上是增函数, 所以; (2)若, 结合图象,可知: 当时,,即, 当时,,即, . 22.定义在R的函数满足对任意恒有且不恒为. (1)求的值; (2)判断的奇偶性并加以证明; (3)若时,是增函数,求满足不等式的的集合. 解:(1)令得,令,得; (2)令,对得即,而不恒为, 是偶函数; (3)又是偶函数,,当时,递增,由,得的取值范围是.查看更多