- 2021-06-16 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习北师大版 不等式选讲 学案
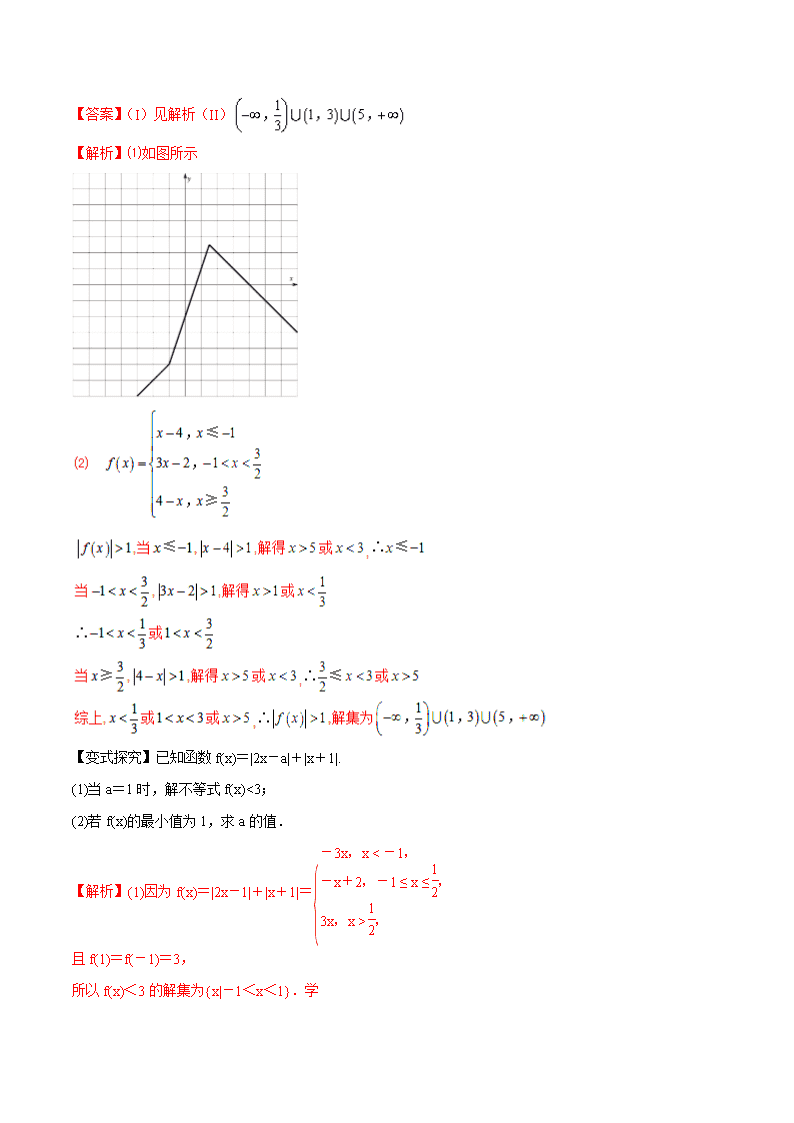
【命题热点突破一】含绝对值的不等式的解法 例1、【2017课标3,理23】已知函数f(x)=│x+1│–│x–2│. (1)求不等式f(x)≥1的解集; 【答案】(1) ; (2) 【变式探究】【2016高考新课标1卷】(本小题满分10分),选修4—5 不等式选讲 已知函数. (I)在答题卡第(24)题图中画出的图像; (II)求不等式的解集. 【答案】(I)见解析(II) 【解析】⑴如图所示 【变式探究】已知函数f(x)=|2x-a|+|x+1|. (1)当a=1时,解不等式f(x)<3; (2)若f(x)的最小值为1,求a的值. 【解析】(1)因为f(x)=|2x-1|+|x+1|= 且f(1)=f(-1)=3, 所以f(x)<3的解集为{x|-1<x<1}.学 (2)|2x-a|+|x+1|=|x-|+|x+1|+|x-|≥|1+|+0=|1+|, 当且仅当(x+1)(x-)≤0且x-=0时,取等号. 所以|1+|=1,解得a=-4或0. 【特别提醒】解含有绝对值的不等式的基本解法是分段去绝对值后,转化为几个不等式组的解,最后求并集得出原不等式的解集. 【变式探究】 已知函数f(x)=2|x+2|-|x-a|(a∈R). (1)当a=4时,求不等式f(x)≤0的解集; (2)当a>-2时,若函数f(x)的图像与x轴所围成的封闭图形的面积不超过54,求a的最大值. 【解析】(1)当a=4时,f(x)≤0,即2|x+2|-|x-4|≤0,即2|x+2|≤|x-4|,两边平方得4x2+16x+16≤x2-8x+16,即x2+8x≤0,解得-8≤x≤0,即不等式f(x)≤0的解集为[-8,0].(或者分段去绝对值求解) 【命题热点突破二】不等式的证明 例2、【2017课标II,理23】已知。证明 (1); (2)。 【答案】(1)证明略;(2)证明略。 【解析】(1) (2)因为 所以,因此a+b≤2. 【变式探究】【2016高考新课标2理数】 已知函数,为不等式的解集. (Ⅰ)求; (Ⅱ)证明 当时,. 【答案】(Ⅰ);(Ⅱ)详见解析. 【解析】(I) 当时,由得解得; 当时, ; 当时,由得解得. 所以的解集. 【变式探究】[2015·全国卷Ⅱ] 设a,b,c,d均为正数,且a+b=c+d,证明 (1)若ab>cd,则+>+; (2)+>+是|a-b|<|c-d|的充要条件. 证明 (1)(+)2=a+b+2 , (+)2=c+d+2 , 由题设a+b=c+d,ab>cd, 得(+)2>(+)2, 因此+>+. 【特别提醒】证明不等式的基本方法有综合法、分析法、反证法、放缩法、数学归纳法等.不等式的性质和重要不等式是证明其他不等式的主要工具,要特别注意柯西不等式的应用. 【变式探究】 (1)已知a,b都是正实数,求证 +≥2 -2. (2)已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+3c2+6d2=5,求a的取值范围. 【解析】(1)证明 方法一 (代数换元法)设a+2b=x,a+b=y,则a=2y-x,b=x-y,且x,y为正实数. +=+=+-2≥2 -2,当且仅当x=y时取等号.学 方法二 (配凑法)+=+1++1-2=+-2≥2 -2,当且仅当a+2b=(a+b)时取等号. (2)由柯西不等式得(2b2+3c2+6d2)≥(b+c+d)2,即2b2+3c2+6d2≥(b+c+d)2.由条件可得5-a2≥(3-a)2,解得1≤a≤2,即a的取值范围是[1,2]. 【命题热点突破三】 绝对值不等式与不等式证明的综合 例3 、【2017课标1,理】已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│. (1)当a=1时,求不等式f(x)≥g(x)的解集; (2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围. 【答案】(1);(2). 【解析】 (2)当时, . 所以的解集包含,等价于当时. 又在的学 最小值必为与之一,所以且,得. 所以的取值范围为. 【变式探究】【2016高考新课标2理数】 已知函数,为不等式的解集. (Ⅰ)求; (Ⅱ)证明 当时,. 【答案】(Ⅰ);(Ⅱ)详见解析. 【解析】(I) 当时,由得解得; 当时, ; 当时,由得解得. 所以的解集. 【变式探究】已知函数f(x)=的定义域为R. (1)求实数m的取值范围; (2)若m的最大值为n,当正数a,b满足+=n时,求7a+4b的最小值. 【解析】(1)因为该函数的定义域为R,所以|x+1|+|x-3|-m≥0恒成立. 设函数g(x)=|x+1|+|x-3|,则m不大于函数g(x)的最小值, 又|x+1|+|x-3|≥|(x+1)-(x-3)|=4,即g(x)的最小值为4,所以m≤4. (2)由(1)知n=4, 所以7a+4b== =≥=,当且仅当a+2b=3a+b,即b=2a=时,等号成立. 所以7a+4b的最小值为.学 【特别提醒】使用绝对值三角不等式求含有两个绝对值符号的函数的最值时,注意利用恒等变换的方法创造使用重要不等式(均值不等式、柯西不等式等)的条件. 【变式探究】 已知函数f(x)=|x|-2|x-3|. (1)求不等式f(x)≥-10的解集; (2)记f(x)的最大值为m,且a,b,c为正实数,求证 当a+b+c=m时,ab+bc+ca≤m≤a2+b2+c2. 【解析】(1)f(x)=|x|-2|x-3|= 当x≤0时,x-6≥-10,∴-4≤x≤0; 当0查看更多